Champ vectoriel

Qu’est-ce qu’un champ vectoriel ?

Un champ vectoriel est une fonction F qui associe à chaque point de l’espace un vecteur. $$ \vec{v} = F(x,y,z) $$

Autrement dit, en tout point de l’espace tridimensionnel (x,y,z), trois composantes scalaires définissent la direction et l’intensité du vecteur selon les axes x, y et z.

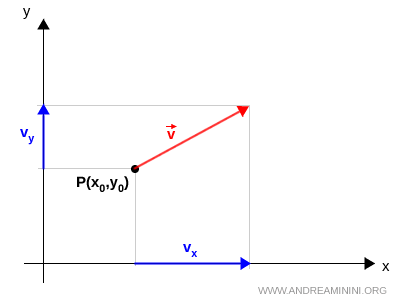
Dans un espace bidimensionnel (x,y), chaque point est associé à deux composantes scalaires : les projections du vecteur sur les axes x et y.

Les vecteurs sont-ils identiques en tout point ou varient-ils ?

Dans un champ vectoriel, les vecteurs peuvent changer de direction, d’orientation et de norme d’un point à l’autre, ou bien rester constants sur toute la région étudiée.

Voici un exemple d’un champ vectoriel défini sur une portion du plan (espace bidimensionnel) :

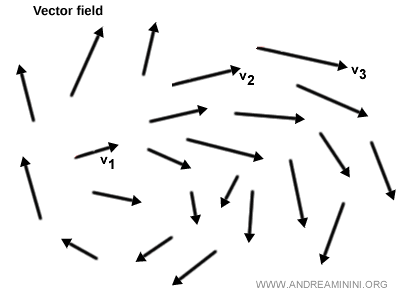
Exemple. Le vent sur une carte météorologique : en chaque point, une flèche indique la direction et l’intensité du vent. C’est un exemple classique de champ vectoriel.

Si tous les vecteurs sont identiques, on parle de champ vectoriel constant.

Un exemple bien connu est le champ gravitationnel près de la surface terrestre.

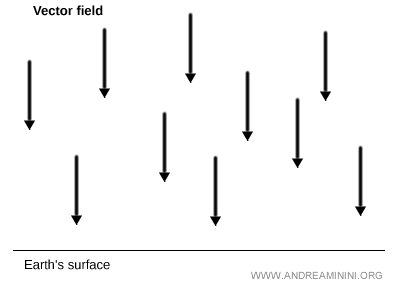
Un champ vectoriel peut aussi être défini dans l’espace euclidien tridimensionnel.

On peut par exemple représenter la direction, le sens et l’intensité d’un flux d’air autour d’une sphère :

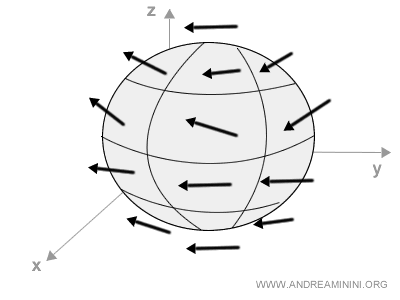
Dans ce cas, chaque vecteur possède trois composantes correspondant à ses projections sur les axes x, y et z :

$$\vec{v}(x, y, z) = \begin{pmatrix} v_x(x,y,z) \\ v_y(x,y,z) \\ v_z(x,y,z) \end{pmatrix}$$

Plus généralement, un champ vectoriel peut aussi dépendre du temps. On introduit alors une quatrième variable : $ F(x, y, z, t) $.

Un exemple pratique

Considérons le champ vectoriel suivant :

$$\vec{v}(x,y,z) = (2x,\ -y,\ 3z)$$

Quelles sont les composantes scalaires du vecteur au point $(1,2,3)$ ?

Les coordonnées du point sont :

$$(x_0, y_0, z_0) = (1,2,3)$$

En les substituant dans l’expression du champ :

$$ \vec{v}(1,2,3) = (2 \cdot 1,\ -2,\ 3 \cdot 3)$$

$$ \vec{v}(1,2,3) = (2, -2, 9)$$

Les composantes du vecteur - c’est-à-dire les valeurs scalaires qui le caractérisent au point $(1,2,3)$ - sont :

$$v_x = 2 $$

$$ v_y = -2 $$

$$ v_z = 9 $$

Donc :

$$\vec{v}(1,2,3) = (2,\ -2,\ 9)$$

Cela signifie qu’au point $(1,2,3)$, le vecteur possède une composante $+2$ selon x, $-2$ selon y, et $+9$ selon z.

Graphiquement, ce vecteur se représente par une flèche partant du point $(1,2,3)$ et pointant vers $(3,0,12)$, somme des coordonnées du point et des composantes du vecteur :

$$ (1,2,3)+(2,-2,9)=(1+2, 2-2, 3+9) = (3,0,12) $$

Ce qui donne la représentation suivante dans l’espace tridimensionnel :

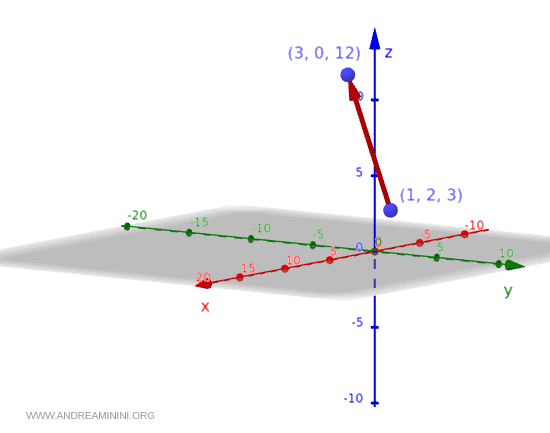
Le même procédé peut être appliqué à tous les points du domaine du champ vectoriel :

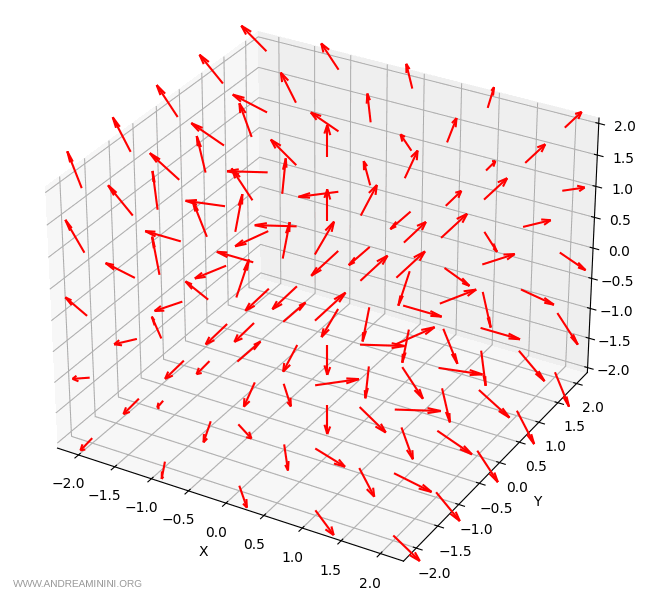
Remarque. Dans la représentation finale, les vecteurs ont été normalisés : ils apparaissent avec une longueur identique afin de faciliter la lecture. Les directions sont correctes, mais la longueur tracée ne correspond pas à la norme réelle des vecteurs.

Différence entre un champ vectoriel et un espace vectoriel

Confondre un champ vectoriel avec un espace vectoriel est une erreur fréquente chez les débutants.

Bien que les deux termes se ressemblent, ils désignent des concepts profondément différents.

• Espace vectoriel
  Un espace vectoriel (ou espace linéaire) est un ensemble d’éléments appelés « vecteurs », que l’on peut additionner et multiplier par des scalaires (nombres réels ou complexes, par exemple), en respectant un ensemble d’axiomes. Ces vecteurs ne se limitent pas à des flèches géométriques : ils peuvent aussi être des fonctions, des matrices ou d’autres objets mathématiques. C’est une structure algébrique abstraite, définie par les opérations qu’elle autorise.
• Champ vectoriel
  En mathématiques, un champ vectoriel est une fonction qui associe un vecteur à chaque point d’un espace, généralement dans ℝ² ou ℝ³. En physique, le terme est employé dans un sens plus large pour décrire toute correspondance qui attribue un vecteur à chaque point d’une région, même sans formule explicite. Un exemple courant est une carte météorologique représentant la direction et l’intensité du vent dans différentes zones géographiques.

Et ainsi de suite.