Distance entre vecteurs
La distance vectorielle est une mesure qui évalue à quel point deux vecteurs sont éloignés l’un de l’autre dans l’espace. Elle se calcule, en général, à partir de la norme de leur différence : \[ d(\vec{v}, \vec{w}) = |\vec{v} - \vec{w}| \]
On peut illustrer cette idée en considérant deux points dans un espace tridimensionnel - même si le raisonnement reste valable en toute dimension.
Supposons que les coordonnées du premier point soient \(\vec{v} = (x_1, y_1, z_1)\) et celles du second \(\vec{w} = (x_2, y_2, z_2)\).
La distance entre ces deux points est donnée par la norme du vecteur différence \(\vec{v} - \vec{w}\) :
\[ |\vec{v} - \vec{w}| = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2} \]
Cette formule n’est rien d’autre qu’une généralisation directe du théorème de Pythagore à l’espace tridimensionnel.
Remarque. Par défaut, la distance entre deux vecteurs est entendue comme la distance euclidienne, c’est-à-dire la racine carrée de la somme des carrés des différences. Toutefois, d’autres mesures sont parfois utilisées. Par exemple, la distance de Manhattan (ou norme L1) s’écrit \(|x_1 - x_2| + |y_1 - y_2|\), tandis que la distance de Tchebychev (ou norme L∞) est donnée par \(\max(|x_1 - x_2|, |y_1 - y_2|)\).
Exemple
Considérons deux vecteurs dans \(\mathbb{R}^2\) :
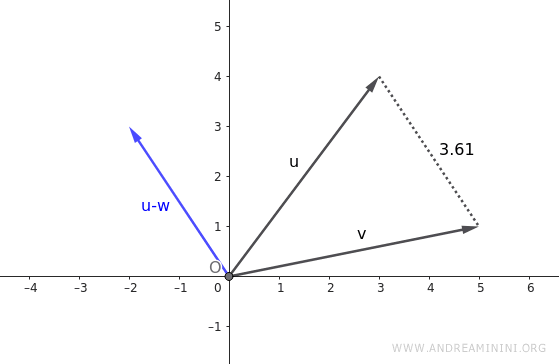
\[ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \]
\[ \vec{w} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \]
Calculons d’abord leur différence :
\[ \vec{v} - \vec{w} = \begin{pmatrix} 3 - 5 \\ 4 - 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
La norme du vecteur différence est alors :
\[ |\vec{v} - \vec{w}| = \sqrt{(-2)^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \]
On obtient donc une distance de \(\sqrt{13}\), soit environ 3,6 unités.
Distance dans des espaces de dimension supérieure
La même formule s’applique sans changement en dimension supérieure.
Par exemple, considérons deux vecteurs de \(\mathbb{R}^4\) :
\[ \vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \]
\[ \vec{b} = \begin{pmatrix} 3 \\ 0 \\ -1 \\ 2 \end{pmatrix} \]
Leur différence vaut :
\[ \vec{a} - \vec{b} = \begin{pmatrix} -2 \\ 2 \\ 4 \\ 2 \end{pmatrix} \]
La distance euclidienne correspondante est :
\[ |\vec{a} - \vec{b}| = \sqrt{(-2)^2 + 2^2 + 4^2 + 2^2} = \sqrt{4 + 4 + 16 + 4} = \sqrt{28} \approx 5,29 \]
Remarque. Dans les espaces de grande dimension, la notion de distance vectorielle joue un rôle central en informatique. Elle sert notamment à mesurer la similarité entre données - qu’il s’agisse d’images, de textes ou de profils d’utilisateurs - et intervient dans des domaines variés comme la modélisation 3D, la reconnaissance de formes ou encore l’apprentissage automatique, en particulier dans les algorithmes des k plus proches voisins (k-NN) et les méthodes de regroupement (clustering).
Et ainsi de suite.