Intégrale de ligne
Une intégrale de ligne (également appelée intégrale curviligne) est une grandeur scalaire obtenue en additionnant les produits scalaires des vecteurs v le long d’une courbe L dans un champ vectoriel C. $$ \int_A^B \vec{v} \cdot dl $$
Ici, dl désigne un déplacement infinitésimal le long de la courbe, allant du point A au point B.
Le vecteur VP représente le vecteur tangent à la courbe en un point P donné.
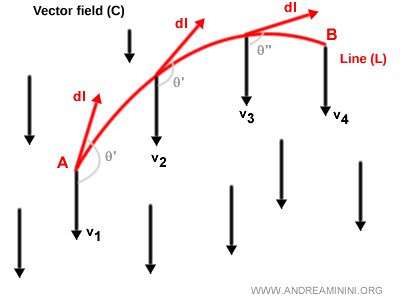
La somme de ces produits scalaires, V·dl, fournit une valeur scalaire appelée intégrale de ligne ou intégrale curviligne.
Applications En physique, les intégrales de ligne sont particulièrement utiles pour calculer le travail nécessaire au déplacement d’un objet dans un champ de forces.
Un exemple concret
Considérons un champ vectoriel constant C, dont tous les vecteurs ont la même norme, la même direction et la même orientation.
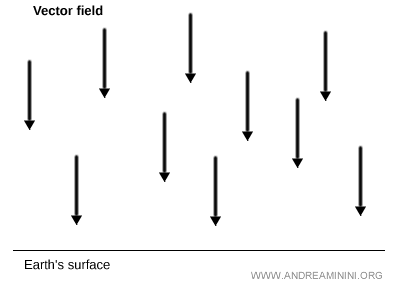
Le champ gravitationnel à proximité de la surface terrestre est un exemple typique d’un tel champ constant.
Les vecteurs indiquent la direction, le sens et l’intensité de la force de gravité (g).
Pour déplacer un objet en ligne droite de A vers B à vitesse constante, il faut fournir un certain travail W afin de compenser l’action de la gravité.
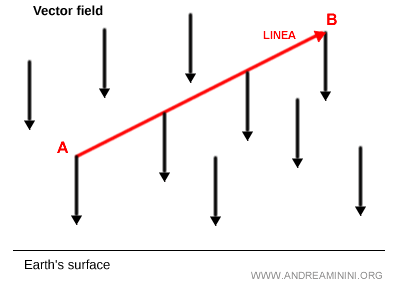
L’intégrale de ligne constitue un moyen de calculer la valeur scalaire du travail effectué par la force F.
Le trajet de A à B est découpé en éléments infinitésimaux dl.
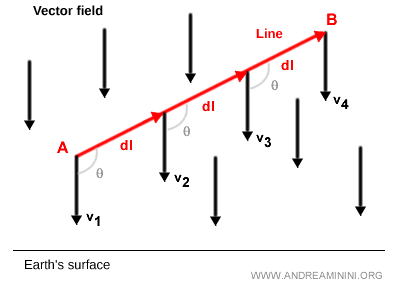
Remarque. Dans cet exemple, la courbe L est une droite. Les vecteurs tangents dl sont donc alignés sur la direction de la trajectoire. $$ W = F \cdot dl $$
En chaque point P, on calcule le produit scalaire entre le vecteur tangent à la trajectoire et le vecteur du champ gravitationnel en P :
$$ \vec{v_1} \cdot dl = |v_1| \cdot |dl| \cdot \cos \theta $$
$$ \vec{v_2} \cdot dl = |v_2| \cdot |dl| \cdot \cos \theta $$
$$ \vec{v_3} \cdot dl = |v_3| \cdot |dl| \cdot \cos \theta $$
La somme de ces produits scalaires correspond à l’intégrale de ligne, c’est-à-dire au travail total W nécessaire pour déplacer l’objet de A à B.
$$ \int_A^B \vec{v} \ dl = \sum_p \vec{v}_p \cdot dl $$
Exemple 2
Le même raisonnement s’applique à un champ vectoriel non constant.
Par exemple, la force gravitationnelle diminue avec l’altitude en s’éloignant de la Terre.
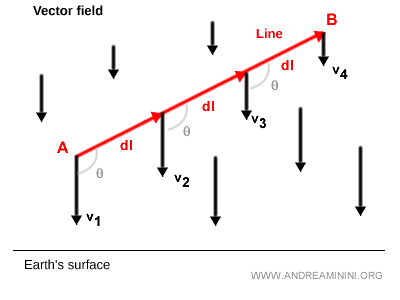
Dans ce cas, la norme des vecteurs décroît à mesure que l’on s’élève.
Le produit scalaire varie donc tout au long du parcours.
Exemple 3
Si la trajectoire n’est pas rectiligne, elle suit une courbe.
Il faut alors calculer le vecteur tangent dl en chaque point de cette courbe.
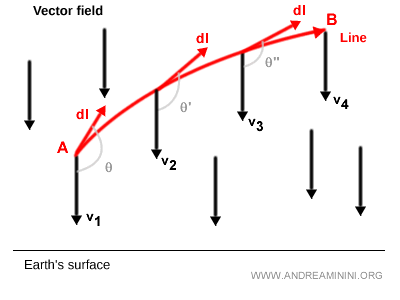
Les vecteurs tangents varient alors en direction, en norme et en orientation.
L’angle \(\theta\) entre le vecteur tangent et le vecteur du champ varie également de façon continue tout au long de la courbe.
En conséquence, le produit scalaire change d’un point à l’autre.
Remarque. Pour estimer la valeur de l’intégrale de ligne, on peut aussi utiliser une approximation polygonale de la courbe : on calcule alors les produits scalaires à l’aide des vecteurs de cette approximation plutôt qu’avec les vecteurs tangents exacts. 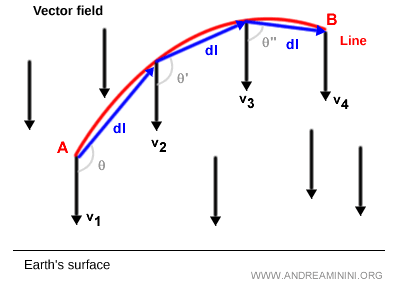
Chaque produit scalaire représente une contribution élémentaire de travail. Leur somme fournit une approximation du travail total. Plus les segments dl de la trajectoire polygonale sont petits, plus l’approximation de l’intégrale de ligne est précise.
Exemple 4
Le même principe vaut pour des champs vectoriels plus complexes.
Par exemple, lorsqu’on se déplace dans une région soumise à des courants d’air ou d’eau variables.
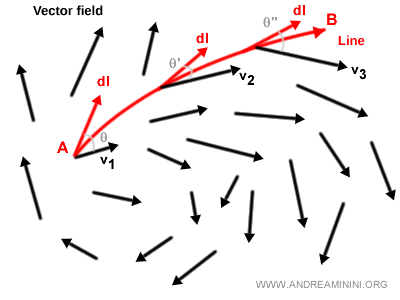
Là encore, le produit scalaire varie continuellement le long de la trajectoire.
Propriétés des intégrales de ligne
Les intégrales de ligne possèdent les mêmes propriétés que les intégrales définies classiques.
- Si l’on choisit un point intermédiaire C dans l’intervalle [A,B], la somme des intégrales de ligne sur les deux sous-arcs [A,C] et [C,B] est égale à l’intégrale de ligne de A à B (propriété d’additivité). $$ \int_A^B \vec{v} \ \cdot dl = \int_A^C \vec{v} \ \cdot dl + \int_C^B \vec{v} \cdot \ dl $$
- Inverser le sens du parcours le long de la trajectoire change le signe de l’intégrale de ligne. $$ \int_A^B \vec{v} \ \cdot dl = - \int_B^A \vec{v} \cdot \ dl $$
Circulation
La circulation correspond au cas où les extrémités de la courbe L coïncident, c’est-à-dire lorsque A = B et que la courbe est fermée. $$ \oint_{L} \vec{v} \cdot dl $$
Dans ce cas, le point initial et le point final de la courbe L se confondent.
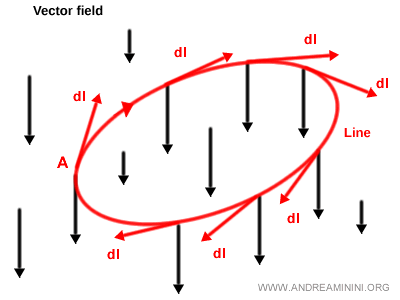
Pour noter l’intégrale de ligne en cas de circulation, on utilise le symbole particulier ∮.
$$ \oint_{L} \vec{v} \cdot dl = \int_A^A \vec{v} \cdot dl $$
Inverser le sens de parcours le long de la courbe fermée L inverse le signe de l’intégrale de ligne.
Et ainsi de suite.