Vecteur équipollent

On dit que deux vecteurs AB et CD sont équipollents lorsqu’ils ont la même norme, la même direction et le même sens.

L’équipollence définit une relation d’équivalence.

Deux vecteurs équipollents ne sont pas obligés d’avoir le même point d’origine. Ils peuvent être placés en des positions différentes dans le plan ou dans l’espace, à condition de conserver les mêmes caractéristiques géométriques.

Propriétés des vecteurs équipollents

Les vecteurs équipollents présentent les propriétés suivantes :

• Propriété réflexive. Tout vecteur est équipollent à lui-même.
• Propriété symétrique. Si le vecteur AB est équipollent au vecteur CD, alors le vecteur CD est équipollent au vecteur AB.
• Propriété transitive. Si le vecteur AB est équipollent au vecteur CD et que le vecteur CD est équipollent au vecteur EF, alors le vecteur AB est équipollent au vecteur EF.

Classe d’équivalence

Dans le plan, l’ensemble des vecteurs équipollents constitue ce que l’on appelle une classe d’équivalence.

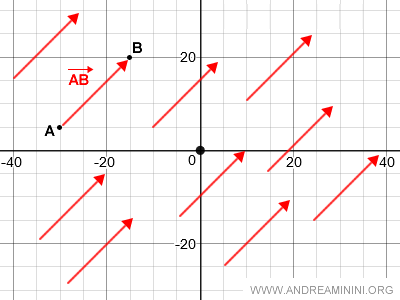
Chaque classe d’équivalence porte le nom générique de vecteur.

Elle regroupe tous les vecteurs du plan qui possèdent la même norme, la même direction et le même sens.