Espaces vectoriels

Qu’est-ce qu’un espace vectoriel ?

Un espace vectoriel sur un corps K est un ensemble non vide V, dont les éléments sont appelés vecteurs, muni de deux opérations (l’addition vectorielle et la multiplication par un scalaire) qui satisfont à un ensemble d’axiomes.

On parle aussi d’espace linéaire ou d’espace vectoriel sur K.

D’un point de vue intuitif, on peut voir un espace vectoriel comme l’ensemble de tous les vecteurs issus d’un point d’origine commun, muni des opérations d’addition et de multiplication par un scalaire.

Remarque. Les éléments d’un espace vectoriel sont en général appelés vecteurs. Toutefois, le terme recouvre des réalités plus larges : un espace vectoriel peut aussi être constitué de matrices ou de polynômes, par exemple.

Quels sont les constituants d’un espace vectoriel ?

Un espace vectoriel est défini par :

• Un corps (K), dont les éléments sont les scalaires.
• Un ensemble non vide (V), dont les éléments sont les vecteurs.
• Deux opérations : l’addition vectorielle et la multiplication par un scalaire, qui doivent vérifier les propriétés suivantes :
  • Commutativité $$ \vec{v}+\vec{w}=\vec{w}+\vec{v} \ \ \ \ \ \ \vec{v}, \vec{w} \in V $$
  • Associativité $$ ( \vec{u}+\vec{v} ) +\vec{w} = \vec{u} + ( \vec{v}+\vec{w} ) \ \ \ \ \ \ \vec{u}, \vec{v}, \vec{w} \in V $$
  • Existence d’un vecteur nul $$ \exists \ \vec{0} \in V \ \ | \ \ \vec{v}+\vec{0} = \vec{v} $$
  • Existence d’un opposé $$ \forall \ \vec{v} \ \ \exists \ -\vec{v} \in V \ \ | \ \ \vec{v}+(-\vec{v}) = \vec{0} $$
  • Compatibilité de la multiplication scalaire $$ (a \cdot b) \cdot \vec{v} = a \cdot (b \cdot \vec{v}) \ \ \ \ a,b \in K,\ \vec{v} \in V $$

    Remarque. Le point « · » désigne deux opérations distinctes : $a*b$ est le produit de deux scalaires dans K, tandis que $(a*b)\vec{v}$ désigne la multiplication du scalaire $(a*b)$ par le vecteur $\vec{v}$.

  • Distributivité $$ (a + b) \cdot \vec{v} = a \cdot \vec{v} + b \cdot \vec{v} \ \ \ \ a,b \in K,\ \vec{v} \in V $$ $$ a \cdot (\vec{v} + \vec{w}) = a \cdot \vec{v} + a \cdot \vec{w} \ \ \ \ a \in K,\ \vec{v}, \vec{w} \in V $$
  • Élément neutre de la multiplication scalaire $$ 1 \cdot \vec{v} = \vec{v} \ \ \ \ \forall \vec{v} \in V $$

Il est important de distinguer les deux niveaux d’opérations : dans le corps K, les opérations concernent uniquement les scalaires, tandis que dans V, elles concernent les vecteurs (ou vecteurs et scalaires). Les propriétés des scalaires relèvent de la structure de corps, celles des vecteurs de la structure d’espace vectoriel.

 

Qu’est-ce qu’un corps ? En mathématiques, un corps est une structure algébrique composée d’un ensemble non vide K et de deux opérations binaires, l’addition (+) et la multiplication (*).

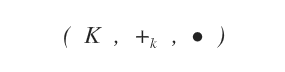
Si K est l’ensemble des réels R, on parle d’espace vectoriel réel. Si K est l’ensemble des complexes C, on parle d’espace vectoriel complexe.

Exemples d’espaces vectoriels

Exemple 1 : L’espace vectoriel R¹

L’espace vectoriel R¹ est un espace de dimension 1 (n=1) sur le corps des réels K=R. Les opérations d’addition vectorielle et de multiplication par un scalaire y sont définies.

Comme n=1, cet espace s’identifie au corps des réels lui-même.

$$ R^1 = \{ (a_1) \ |\ a_1 \in R \} $$

Chaque point de la droite correspond à un nombre réel.

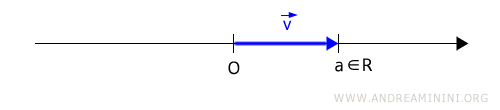
Avec une origine fixée (O), chaque point de la droite représente un vecteur dont la norme (ou module) est égale à un réel.

Remarque. Dans R¹, tous les vecteurs ont la même direction, sont orientés dans un sens ou dans l’autre, et ne diffèrent que par leur longueur.

Exemples de vecteurs de R¹ :

$$ \vec{v_1} = 3 \ \ \ \ \vec{v_2} = 5 \ \ \ \ \vec{v_3} = -1 \ \ \ ... $$

Les opérations d’addition et de multiplication par un scalaire dans R¹ respectent bien les axiomes des espaces vectoriels.

Exemple 2 : L’espace vectoriel R²

Lorsque n=2, l’espace vectoriel R² (soit RxR) correspond au plan cartésien des réels.

$$ R^2 = \{ (a_1,a_2) \ |\ a_1,a_2 \in R \} $$

Chaque couple de réels (x,y) correspond à un point du plan euclidien, c’est-à-dire à un vecteur de dimension 2.

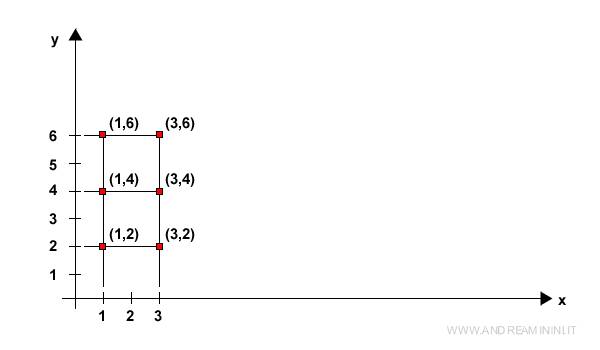
L’espace vectoriel réel est donc constitué de tous les vecteurs de R².

Exemples de vecteurs de R² :

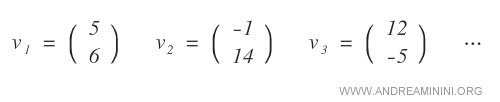
Remarque. Comme l’ensemble des réels R est infini, l’espace vectoriel R² l’est également.

Dans R², les deux opérations définies sont l’addition vectorielle et la multiplication par un scalaire.

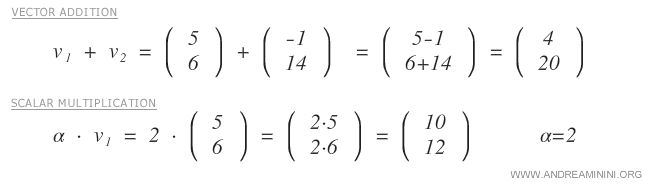
Toutes ces opérations respectent les axiomes des espaces vectoriels.

On établit ainsi que R² est un espace vectoriel sur le corps R.

Le même raisonnement s’applique à tout espace vectoriel réel Rⁿ, formé de vecteurs à n composantes réelles.

Exemple 3 : L’espace vectoriel R³

Lorsque n=3, l’espace vectoriel R³ (c’est-à-dire RxRxR) correspond à l’espace tridimensionnel usuel.

$$ R^3 = \{ (a_1,a_2,a_3) \ |\ a_1,a_2,a_3 \in R \} $$

Chaque triplet de réels (x,y,z) définit un point de l’espace, autrement dit un vecteur de dimension 3 où a₁=x, a₂=y et a₃=z.

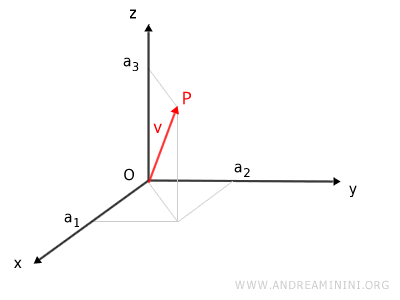
Dans R³, les deux opérations fondamentales (addition vectorielle et multiplication par un scalaire) sont bien définies.

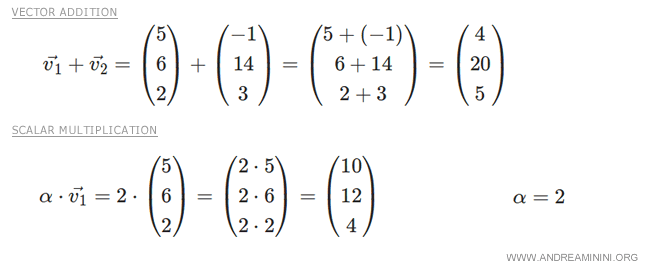
Elles satisfont toutes les propriétés caractéristiques des espaces vectoriels.

Exemple 4 : L’espace vectoriel R⁴

Lorsque n=4, l’espace vectoriel R⁴ (soit RxRxRxR) est un espace de dimension quatre.

Il est constitué de vecteurs à quatre composantes (a₁, a₂, a₃, a₄).

$$ R^4 = \{ (a_1,a_2,a_3,a_4) \ |\ a_1,a_2,a_3,a_4 \in R \} $$

Dans R⁴, l’addition vectorielle et la multiplication par un scalaire sont définies de manière analogue aux cas précédents et vérifient les axiomes d’espace vectoriel.

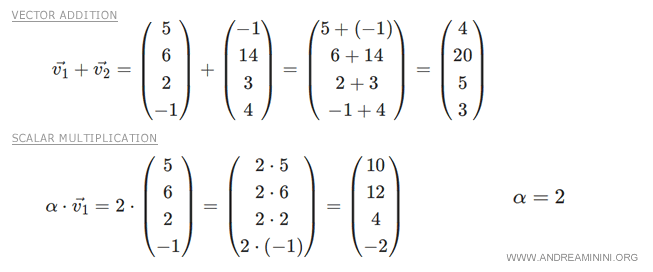
Remarque. Se représenter un espace de dimension quatre (ou plus) dépasse notre intuition géométrique, limitée à trois dimensions. En revanche, il est aisé de concevoir les cas de dimension 1 ou 2. Quoi qu’il en soit, les espaces vectoriels existent rigoureusement en toute dimension.

Exemple 5 : L’espace vectoriel Rⁿ

L’espace vectoriel Rⁿ est défini comme le produit cartésien RxRx...xR (n fois).

$$ R^n = \{ (a_1,a_2,\dots,a_n) \ |\ a_i \in R \} $$

Chaque élément de Rⁿ est un vecteur à n composantes, autrement dit un n-uplet ordonné de réels a₁,...,a_n.

$$ \vec{v} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{pmatrix} \ \ \ \ \vec{v} \in V = R^n $$

Ainsi, Rⁿ est l’espace des n-uplets réels, muni des opérations suivantes :

1. Addition de deux vecteurs v₁ et v₂, qui donne un vecteur de Rⁿ.
   
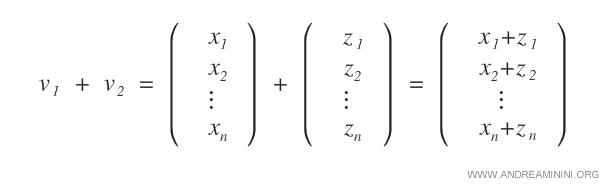
2. Multiplication d’un vecteur v par un scalaire α, qui produit également un vecteur de Rⁿ.
   

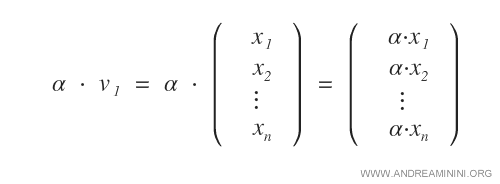
Ces opérations respectent l’ensemble des axiomes d’un espace vectoriel.

Remarque. Les propriétés fondamentales d’un espace vectoriel sont : associativité, commutativité, distributivité (par rapport à l’addition vectorielle et à l’addition scalaire), existence d’un élément neutre, existence d’un opposé additif, compatibilité de la multiplication scalaire et identité de la multiplication scalaire.

Norme et produit scalaire

La simple structure d’espace vectoriel n’implique pas les notions de longueur d’un vecteur ni d’angle entre deux vecteurs.

Pour introduire ces concepts, il faut enrichir l’espace de structures supplémentaires, reposant sur deux notions :

• La norme, qui attribue à chaque vecteur une longueur (ou magnitude).
• Le produit scalaire, qui permet de définir l’angle entre deux vecteurs.

Remarque. Il existe plusieurs manières de définir une norme ou un produit scalaire. Selon le choix effectué, la notion de longueur et d’angle varie : il n’existe pas une définition unique.

Combinaison linéaire

L’une des opérations centrales dans un espace vectoriel est la combinaison linéaire.

Une combinaison linéaire est une opération qui associe des vecteurs et des scalaires dans un espace vectoriel V défini sur un corps K=R : $$ \vec{w} = a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + \dots + a_n \cdot \vec{v_n} $$ On obtient ainsi un vecteur w, somme pondérée de n vecteurs par n scalaires.

Autrement dit : $$ \vec{w}, \vec{v_1}, \vec{v_2}, ..., \vec{v_n} \in V \qquad a_1, a_2, ..., a_n \in K=R $$

Vecteurs linéairement indépendants et dépendants

Les combinaisons linéaires permettent de distinguer deux cas :

• Vecteurs linéairement indépendants
  Les vecteurs v₁,...,v_n sont indépendants si la seule combinaison qui donne le vecteur nul est la combinaison triviale : $$ a_1\vec{v_1} + a_2\vec{v_2} + \dots + a_n\vec{v_n} = \vec{0} \ \ \Longrightarrow \ \ a_1=a_2=\dots=a_n=0 $$
• Vecteurs linéairement dépendants
  Ils sont dépendants s’il existe une combinaison non triviale (au moins un coefficient non nul) qui conduit au vecteur nul : $$ a_1\vec{v_1} + a_2\vec{v_2} + \dots + a_n\vec{v_n} = \vec{0}, \quad \exists \ a_i \neq 0 $$

En d’autres termes, des vecteurs sont dépendants dès lors qu’ils ne sont pas indépendants.

Types d’espaces vectoriels

On distingue deux grandes familles :

• Espaces vectoriels de dimension finie
  Engendrés par un nombre fini de vecteurs.
• Espaces vectoriels de dimension infinie
  Engendrés par une infinité de vecteurs.

Et ainsi de suite.