Vecteurs géométriques
Qu’est-ce qu’un vecteur géométrique ?
Un vecteur géométrique est l’ensemble de tous les segments orientés qui sont équivalents entre eux.
En mathématiques, il s’agit d’une notion abstraite qui formalise la propriété commune à une famille de segments orientés équivalents.
Segments orientés équivalents
Deux segments orientés, tels que AB et CD, sont dits équivalents lorsqu’ils possèdent la même direction, le même sens et la même longueur (également appelée module ou norme).
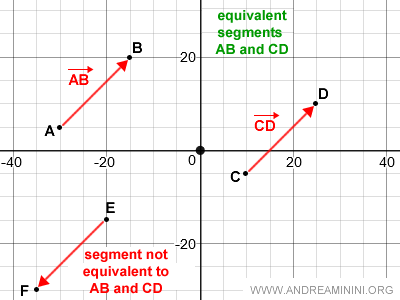
Remarque. Les segments AB et CD sont équivalents car ils coïncident en direction, en sens et en longueur. En revanche, le segment EF ne l’est pas : bien qu’il ait la même direction et la même longueur, son sens est opposé.
La relation d’équivalence entre deux segments orientés s’exprime ainsi :
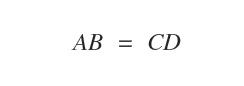
En translatant le segment AB dans le plan cartésien, on obtient une infinité de segments équivalents.
L’ensemble de tous les segments équivalents à AB, obtenus par translation, définit un vecteur géométrique.
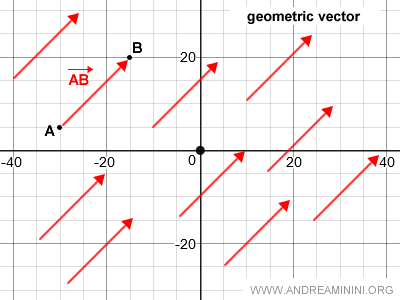
On peut donc énoncer :
Étant donnée une direction, un sens et une norme, il existe un unique vecteur géométrique possédant ces caractéristiques.
En conclusion, un vecteur géométrique est un objet abstrait qui représente une classe de segments orientés équivalents.
Différence entre vecteurs libres et vecteurs liés
Un vecteur peut être soit libre, soit lié.
- Un vecteur lié est attaché à un point d’origine déterminé (O).
- Un vecteur libre n’est associé à aucun point précis du plan.
Un vecteur géométrique libre est l’ensemble de tous les vecteurs équivalents au vecteur AB (représentant de la classe).
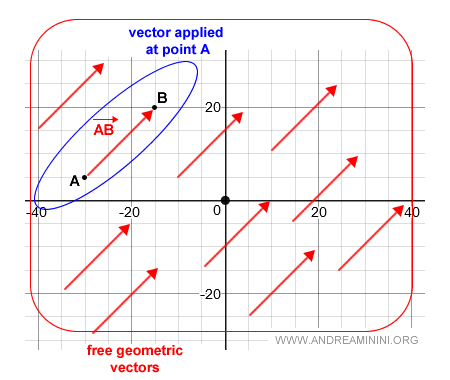
Le vecteur libre représente la classe d’équivalence (ou équipollence) du vecteur lié AB.
Remarque. Le choix du vecteur lié de référence - autrement dit, le représentant de la classe - est entièrement arbitraire.
L’ensemble de tous les vecteurs libres d’un plan constitue ce que l’on appelle l’ensemble quotient.
Addition des vecteurs géométriques
Pour additionner deux vecteurs géométriques libres, on utilise la méthode du parallélogramme, en les plaçant avec une origine commune (O).
Un exemple concret
Dans le plan, les vecteurs géométriques AB et CD appartiennent à deux classes d’équivalence distinctes.
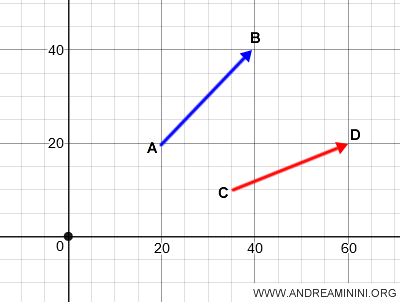
Pour les additionner, on repositionne les deux vecteurs de façon à ce qu’ils partagent le même point d’origine.
Une fois ainsi replacés, les vecteurs AB et CD, ayant pour origine commune O, deviennent OB et OD.
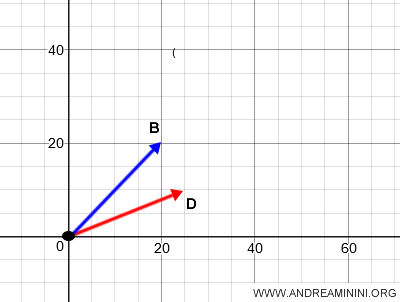
Quel point d’origine choisir ? Si le plan possède déjà une origine définie, comme le point O, il est préférable de s’y référer, car cela simplifie à la fois les calculs et la représentation graphique.
On additionne ensuite les vecteurs OB et OD en appliquant la méthode du parallélogramme.
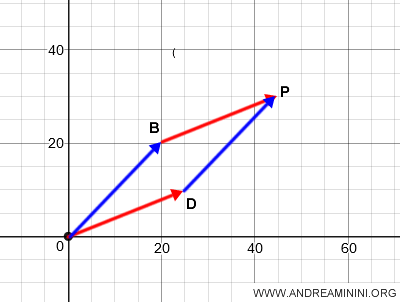
Le résultat de la somme des vecteurs OB et OD est le vecteur OP.
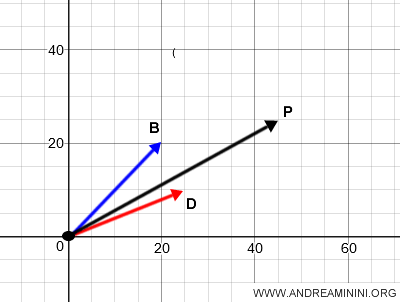
En résumé, le vecteur OP représente la classe d’équivalence correspondant à la somme des vecteurs géométriques libres AB + CD.
Appliqué en tout point du plan, le vecteur OP définit le vecteur géométrique libre résultant.