Union de sous-espaces vectoriels

L’union de deux sous-espaces vectoriels n’est, en général, pas un sous-espace vectoriel.

Soit V un espace vectoriel sur un corps K, et soient A et B deux de ses sous-espaces. En règle générale, l’union A ∪ B n’est pas un sous-espace vectoriel.

Pourquoi ?

Parce que l’union A ∪ B n’est pas fermée pour l’addition vectorielle :

$$ \vec{a} + \vec{b} \notin A \cup B $$

Elle est seulement fermée pour la multiplication scalaire :

$$ k \cdot \vec{a} \in A \cup B $$

Démonstration

Soient A et B deux sous-espaces de V. On cherche à savoir si leur union A ∪ B est encore un sous-espace.

Pour que ce soit le cas, il faudrait notamment que : si $\vec{a}, \vec{b} \in A \cup B$, alors $\vec{a} + \vec{b} \in A \cup B$.

$$ \forall \ \vec{a} \in A , \vec{b} \in B \ \Rightarrow\ \vec{a} + \vec{b} \in A \cup B $$

Or cette condition est en général fausse.

Ainsi, A ∪ B ne satisfait pas les axiomes définissant un sous-espace. 

Exemple

Considérons l’espace vectoriel ℝ².

Le plan cartésien (x, y), formé de points de ℝ×ℝ ( ℝ² ), est un espace vectoriel usuel.

Soient X et Y deux sous-espaces, par exemple l’axe X et l’axe Y :

$$ X = \left\{ \binom{x}{y} \in ℝ^2 \mid y = 0 \right\} $$

$$ Y = \left\{ \binom{x}{y} \in ℝ^2 \mid x = 0 \right\} $$

Ce sont bien deux sous-espaces vectoriels de V, puisqu’ils vérifient les axiomes de sous-espace et correspondent à des systèmes linéaires homogènes.

Remarque. Comme ce sont des sous-espaces unidimensionnels, leur représentation graphique est immédiate et rend le concept plus clair.

L’union X ∪ Y regroupe tous les vecteurs situés sur l’un ou l’autre des deux axes (en bleu) :

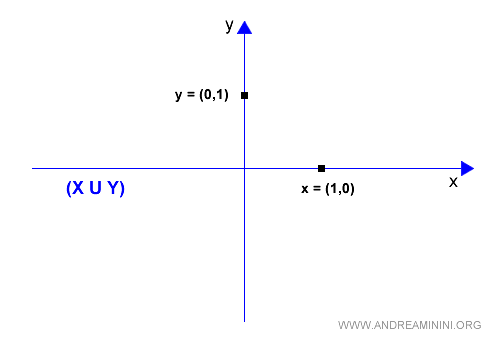
Cependant, cette union n’est pas un sous-espace, car elle n’est pas fermée pour l’addition.

Contre-exemple :

$$ \vec{x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \in X, \qquad \vec{y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \in Y $$

Alors :

$$ \vec{x} + \vec{y} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$

Or $(1,1)$ n’appartient ni à X ni à Y :

$$ \begin{pmatrix} 1 \\ 1 \end{pmatrix} \notin X \quad (y \ne 0) $$

$$ \begin{pmatrix} 1 \\ 1 \end{pmatrix} \notin Y \quad (x \ne 0) $$

D’où :

$$ \vec{x} + \vec{y} \notin X \cup Y $$

L’union ne vérifie donc pas la fermeture pour l’addition.

Remarque. L’union est bien fermée pour la multiplication scalaire (car $k\vec{x} \in X \cup Y$ si $\vec{x} \in X \cup Y$), mais cela ne suffit pas : un sous-espace doit être fermé à la fois pour l’addition et pour la multiplication.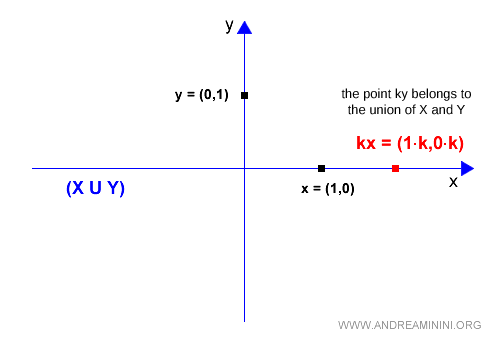

On conclut donc que l’union de deux sous-espaces vectoriels n’est en général pas un sous-espace vectoriel.

Le plus petit sous-espace contenant l’union

La somme A + B est le plus petit sous-espace de V contenant l’union A ∪ B.

Démonstration

Soient A, B ⊆ V deux sous-espaces.

Soit L un sous-espace contenant l’union :

$$ A \cup B \subseteq L \subseteq V $$

Comme L est un sous-espace, il est fermé pour l’addition :

$$ \vec{a}, \vec{b} \in L \ \Rightarrow\ \vec{a} + \vec{b} \in L $$

On a donc :

$$ \{ \vec{a} + \vec{b} \mid \vec{a} \in A, \vec{b} \in B \} \subseteq L $$

Par définition :

$$ A + B \subseteq L $$

Ainsi, tout sous-espace contenant A et B contient nécessairement leur somme A + B.

Or A + B est lui-même un sous-espace (voir la démonstration) ; c’est donc le plus petit sous-espace contenant l’union A ∪ B.

Explication. A + B est contenu dans tout sous-espace de V contenant A et B, il est donc minimal parmi eux.

Remarques

Quelques remarques complémentaires sur l’union de sous-espaces :

• En général, l’union de deux sous-espaces vectoriels n’est pas un sous-espace. Elle l’est toutefois dans des cas particuliers, par exemple si l’un est inclus dans l’autre : $$ X \subseteq Y \ \Rightarrow\ X \cup Y = Y $$ L’union coïncide alors avec le plus grand des deux et constitue bien un sous-espace.