Sous-espaces complémentaires

Deux sous-espaces vectoriels sont dits complémentaires lorsqu’ils forment une somme directe et que leur somme recouvre tout l’espace vectoriel.

Définition des sous-espaces complémentaires

Soient $A$ et $B$ deux sous-espaces de l’espace vectoriel $V$. On dit qu’ils sont complémentaires si :
$$ \begin{cases} A \oplus B \\ A + B = V \end{cases} $$

La première condition (somme directe) implique que l’intersection des deux sous-espaces est triviale :

$$ A \oplus B \;\Rightarrow\; A \cap B = \{0_v\} $$

La seconde condition stipule que la somme des sous-espaces $A+B$ engendre l’espace vectoriel tout entier $V$ :

$$ A + B = V $$

Lorsque ces deux conditions sont réunies, on écrit :

$$ A \oplus B = V $$

Il est essentiel que les deux propriétés soient simultanément vérifiées : ni l’intersection triviale ni la simple somme des sous-espaces, prises isolément, ne suffisent à assurer la complémentarité.

Différence entre somme directe et somme de sous-espaces. La somme directe exige que l’intersection se réduise au seul vecteur nul { 0_v }, tandis que la somme de sous-espaces désigne l’ensemble des combinaisons linéaires de leurs éléments.

Exemples

Examinons quelques cas pour déterminer si deux sous-espaces vectoriels sont complémentaires.

Exemple 1

Soit $V = \mathbb{R}^3$, et considérons :

$$ A = \{ (x,y,z) \in \mathbb{R}^3 \mid x=0,\ y=0 \} $$

$$ B = \{ (x,y,z) \in \mathbb{R}^3 \mid z=0 \} $$

Le sous-espace $A$ correspond à l’axe $z$ (en bleu), tandis que $B$ est le plan $xy$ (en rouge).

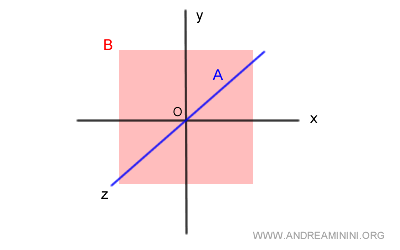
Leur intersection est réduite au vecteur nul :

$$ A \cap B = \{0_v\} $$

On a donc $A$ et $B$ en somme directe :

$$ A \oplus B $$

La première condition est vérifiée.

Vérifions à présent si leur somme engendre tout $V$ :

$$ A + B = V $$

En effet, la translation du plan $B$ le long de l’axe $z$ remplit tout l’espace tridimensionnel.

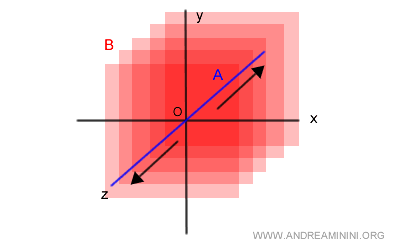
La seconde condition étant également satisfaite, $A$ et $B$ sont complémentaires.

Exemple 2

Dans $V = \mathbb{R}^3$, considérons :

$$ A = \{ (x,y,z) \in \mathbb{R}^3 \mid x=0,\ y=0 \} $$

$$ B = \{ (x,y,z) \in \mathbb{R}^3 \mid z=0,\ y=0 \} $$

Ici, $A$ est l’axe $z$ (en bleu) et $B$ l’axe $x$ (en rouge).

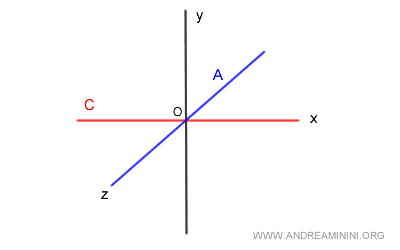
L’intersection est triviale :

$$ A \cap B = \{0_v\} $$

On a donc $A \oplus B$. Mais leur somme ne couvre pas tout $\mathbb{R}^3$ :

$$ A + B = \{ (x,0,z) \in \mathbb{R}^3 \} $$

C’est-à-dire le plan $xz$, et non l’espace complet.

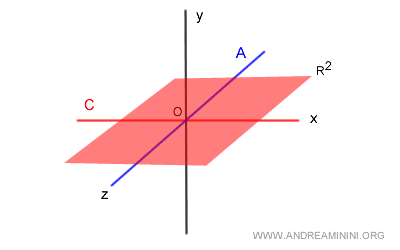
Ainsi, bien qu’en somme directe, $A$ et $B$ ne sont pas complémentaires.

Exemple 3

Dans $\mathbb{R}^3$, considérons :

$$ A = \{ (x,y,z) \in \mathbb{R}^3 \mid x=0,\ y=0 \} $$

$$ C = \{ (x,y,z) \in \mathbb{R}^3 \mid y=0 \} $$

$A$ est l’axe $z$ (en bleu), tandis que $C$ est le plan $xz$ (en rouge).

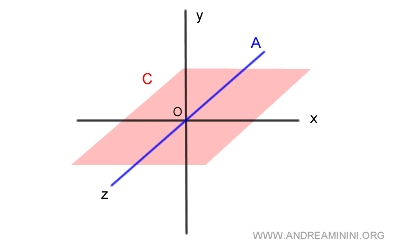
L’intersection vaut :

$$ A \cap C = \{ (0,0,z) \in \mathbb{R}^3 \} $$

Elle n’est pas triviale, puisqu’elle contient tous les vecteurs de l’axe $z$.

Par conséquent, $A$ et $C$ ne sont pas en somme directe.

En conclusion, $A$ et $C$ ne sont pas complémentaires, et il n’est pas nécessaire de vérifier leur somme.