Sous-espace vectoriel

Qu’est-ce qu’un sous-espace vectoriel ?

Un sous-espace vectoriel est un sous-ensemble d’un espace vectoriel qui vérifie toutes les propriétés caractéristiques des espaces vectoriels.

Définition d’un sous-espace vectoriel

Soit V un espace vectoriel sur un corps K. Un sous-ensemble W est appelé sous-espace vectoriel de V $$ W \subseteq V $$ s’il satisfait les conditions suivantes :
1. Pour tous vecteurs w₁ et w₂ de W, leur somme appartient encore à W. $$ \forall \ \vec{w}_1, \vec{w}_2 \in W \ \Rightarrow \ \vec{w}_1 + \vec{w}_2 \in W $$
2. Pour tout scalaire λ de K et tout vecteur w de W, le produit λw reste dans W. $$ \forall \ \lambda \in K, \ \forall \ \vec{w} \in W \ \Rightarrow \ \lambda \cdot \vec{w} \in W $$

En d’autres termes, un sous-espace vectoriel est un sous-ensemble stable par addition de vecteurs et par multiplication par un scalaire.

Tout sous-espace vectoriel constitue lui-même un espace vectoriel.

Ainsi, toutes les propriétés des espaces vectoriels s’appliquent intégralement à tout sous-espace.

Remarque. Il est important de souligner que tout sous-ensemble d’un espace vectoriel n’est pas automatiquement un sous-espace. Pour le vérifier, il convient de contrôler qu’il satisfasse bien les axiomes requis.

Comment reconnaître un sous-espace ?

La première vérification consiste à s’assurer que le sous-ensemble contient le vecteur nul.

Pourquoi est-ce essentiel ?

Parce que l’existence du vecteur nul est l’une des propriétés fondamentales de tout espace vectoriel.

Étant donné que les sous-espaces sont eux-mêmes des espaces vectoriels, ils doivent nécessairement contenir le vecteur nul.

Si un sous-ensemble ne contient pas le vecteur nul, il ne peut pas être un sous-espace vectoriel.

Une fois cette condition remplie, il faut encore vérifier les deux propriétés essentielles : la stabilité par addition et la stabilité par multiplication scalaire.

Un sous-ensemble est un sous-espace vectoriel s’il satisfait ces deux conditions fondamentales :

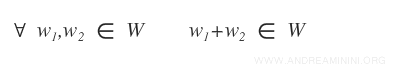
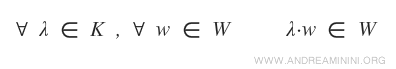
En pratique, il s’agit de vérifier que la somme de deux éléments de W et le produit d’un vecteur de W par un scalaire donnent toujours des vecteurs appartenant à W.

Si ces deux conditions sont remplies, alors W est un sous-espace vectoriel ; sinon, il ne l’est pas.

Exemple concret

Exemple 1

Dans ce premier exemple, nous vérifierons si un sous-ensemble W constitue bien un sous-espace vectoriel.

Exemple 2

Dans le second exemple, nous étudions un autre sous-ensemble.

Ici, l’équation est égale à un, ce qui conduit à une conclusion différente.

Autres exercices corrigés

1. exercice 1
2. exercice 2
3. exercice 3
4. exercice 4

Identification graphique des sous-espaces vectoriels

Il est également possible d’analyser si un sous-ensemble satisfait les conditions de sous-espace à partir de sa représentation graphique dans le plan cartésien.

Si le sous-ensemble W contient le vecteur nul (0,0), sa représentation passe nécessairement par l’origine O.

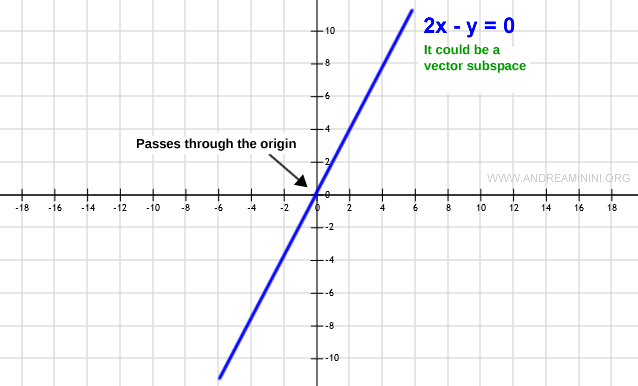
Remarque. Cette condition est nécessaire, mais non suffisante : le fait qu’une droite passe par l’origine ne garantit pas à lui seul qu’il s’agisse d’un sous-espace. Ce n’est qu’une première vérification.

À l’inverse, si la représentation ne passe pas par l’origine, alors le sous-ensemble ne contient pas le vecteur nul.

Dans ce cas, W n’est pas un sous-espace vectoriel.

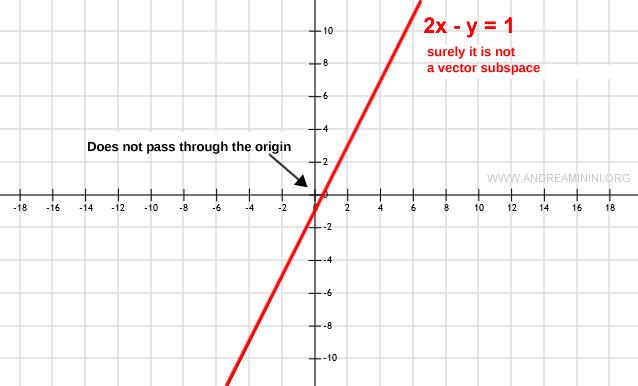
Remarque. Si la représentation ne passe pas par l’origine, le sous-ensemble peut immédiatement être écarté comme sous-espace, sans qu’il soit nécessaire de vérifier d’autres propriétés.

Si au contraire la droite passe par l’origine, il faut encore contrôler que le sous-ensemble vérifie les deux conditions fondamentales.

C’est un sous-espace si...

Le sous-ensemble W est un sous-espace si la somme de deux vecteurs quelconques de W donne un vecteur qui appartient encore à W (c’est-à-dire qui reste sur la droite).

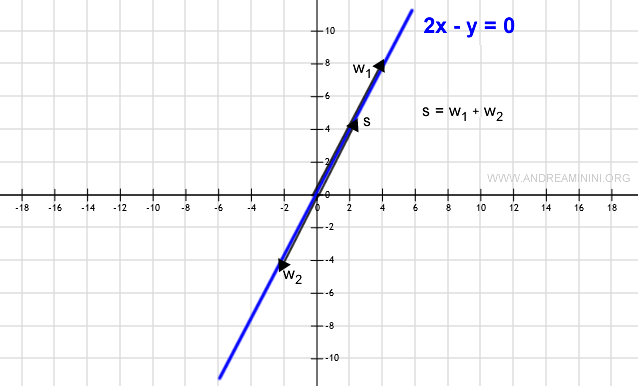
De même, la multiplication d’un vecteur w par un scalaire doit fournir un vecteur qui reste sur la droite (et donc dans W).

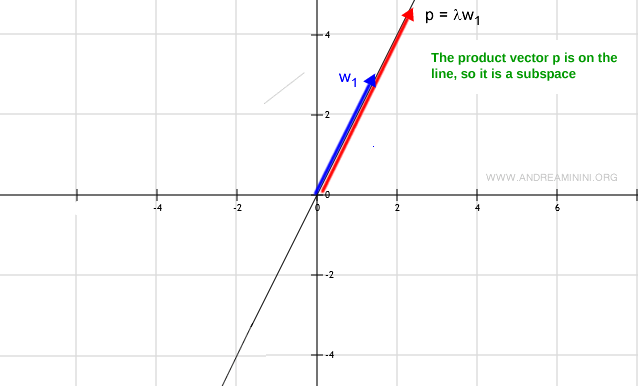
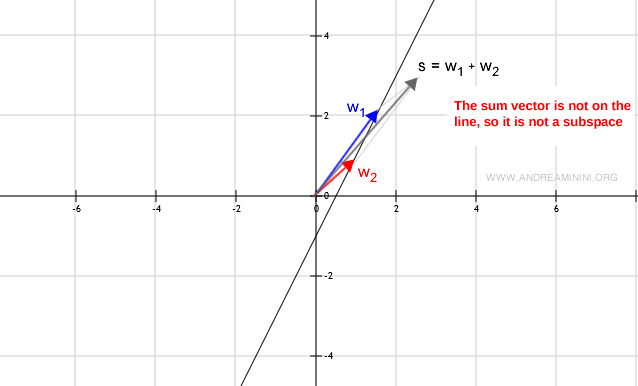
Ce n’est pas un sous-espace si...

W n’est pas un sous-espace si la somme w₁ + w₂ donne un vecteur qui sort de W (par exemple, qui n’appartient pas à la droite).

Ou encore si la multiplication scalaire λw produit un vecteur qui sort de la droite, ce qui viole la condition de stabilité.

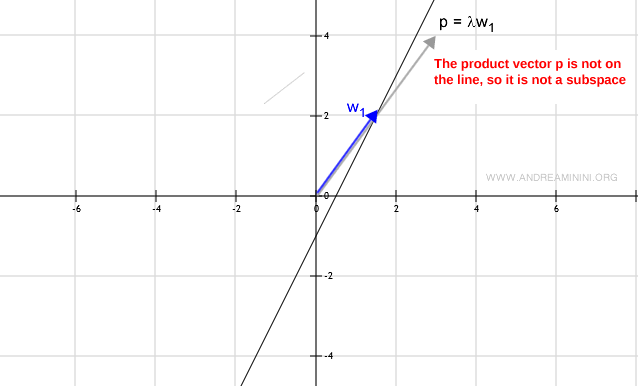
En somme, l’analyse graphique peut constituer un outil pédagogique utile pour identifier les sous-espaces vectoriels.

Sous-espaces vectoriels et combinaisons linéaires

Un sous-ensemble W d’un espace vectoriel V est un sous-espace si toute combinaison linéaire de ses éléments (avec des scalaires de K) appartient également à W.

Cette formulation synthétise de manière élégante les deux propriétés fondamentales d’un sous-espace : la stabilité par addition et par multiplication scalaire.