Enveloppe linéaire (Span)

L’enveloppe linéaire (ou span linéaire) d’un ensemble de vecteurs $v_1, v_2, \dots, v_n$ dans un espace vectoriel $V$ sur un corps $K$ est l’ensemble de toutes les combinaisons linéaires possibles de ces vecteurs, avec des coefficients scalaires $\alpha_1, \alpha_2, \dots, \alpha_n$ appartenant à $K$ : $$ \operatorname{Span}(v_1, \dots, v_n) = \left\{ \alpha_1 v_1 + \cdots + \alpha_n v_n \mid \alpha_i \in K \right\} $$

L’enveloppe linéaire peut également être notée $L_k$, $L$ ou encore à l’aide de crochets angulaires :

$$ L_k(v_1, \dots, v_n) \qquad L(v_1, \dots, v_n) \qquad \langle v_1, \dots, v_n \rangle $$

L’ensemble $\operatorname{Span}(v_1, \dots, v_n)$ est toujours un sous-espace vectoriel de $V$.

On l’appelle aussi le sous-espace engendré par les vecteurs $v_1, \dots, v_n$.

Exemples

Exemple 1

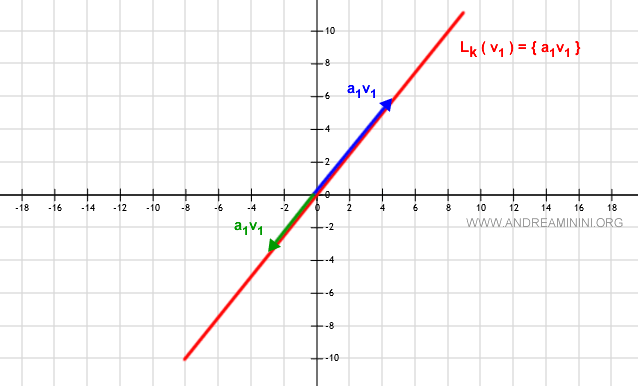
Soit $v_1$ un vecteur non nul d’un espace vectoriel $V$ sur le corps $\mathbb{R}^2$ ($v_1 \ne \vec{0}$). Alors l’enveloppe linéaire $L(v_1)$ est constituée de tous les vecteurs de la forme $\alpha_1 v_1$, avec $\alpha_1 \in \mathbb{R}$, c’est-à-dire l’ensemble des points de la droite passant par l’origine et dirigée par $v_1$.

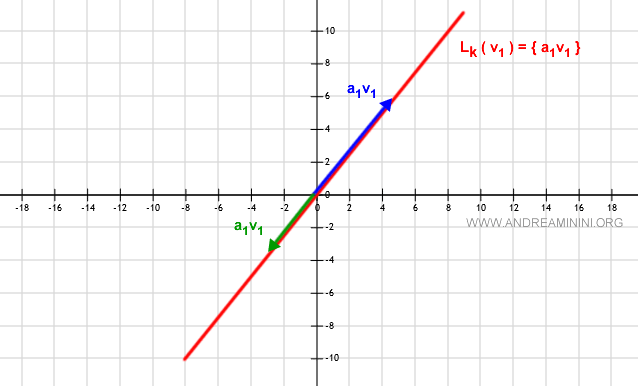
Chaque choix de $\alpha_1$ fournit un vecteur situé sur la droite $L_k$, de même direction que $v_1$, mais de norme et de sens variables, puisque tous sont des multiples scalaires de $v_1$.

Il est donc clair que $L_k$ constitue bien un sous-espace vectoriel de $V$.

Exemple 2

Soient $v_1$ et $v_2$ deux vecteurs de l’espace vectoriel $V$ sur le corps $\mathbb{R}^2$. L’enveloppe linéaire $L_k(v_1, v_2)$ est l’ensemble de tous les vecteurs de la forme $\alpha_1 v_1 + \alpha_2 v_2$, où $\alpha_1, \alpha_2 \in \mathbb{R}$. Autrement dit, elle regroupe toutes les combinaisons linéaires de $v_1$ et $v_2$ dans le plan.

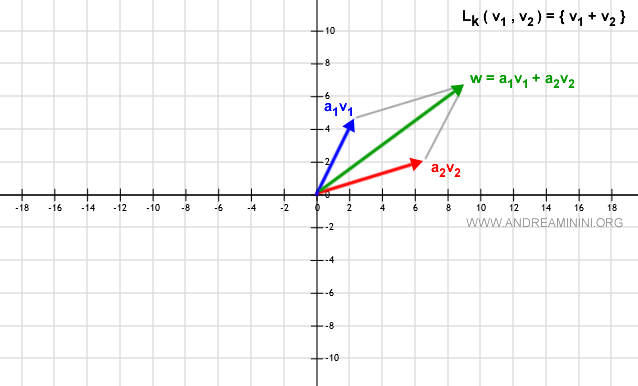
Chaque couple $(\alpha_1, \alpha_2)$ définit un vecteur $w = \alpha_1 v_1 + \alpha_2 v_2$, dont la direction, le sens et la norme varient selon les coefficients choisis.

Si $v_1$ et $v_2$ ne sont pas parallèles, on obtient $w$ en appliquant la règle du parallélogramme : la somme d’un multiple de $v_1$ et d’un multiple de $v_2$.

Dans ce cas, l’ensemble $L_k(v_1, v_2)$ est un sous-espace bidimensionnel de $V$.

Remarque. Si $v_1$ et $v_2$ sont parallèles, on se ramène au cas d’une unique droite passant par l’origine. Les deux vecteurs ont la même direction et engendrent donc le même sous-espace. En effet, toute combinaison linéaire $\alpha_1 v_1 + \alpha_2 v_2$ n’est qu’un multiple d’un seul vecteur. On a alors : $$ \langle v_1, v_2 \rangle = \langle v_1 \rangle $$