Générateurs d’un espace vectoriel

Un système générateur est un ensemble de vecteurs $S = \{ v_1, \dots, v_m \} \subset V$ tel que tout vecteur $v \in V$ puisse s’exprimer comme une combinaison linéaire des éléments de $S$, avec des coefficients $a_1, \dots, a_m \in \mathbb{R}$ : $$ \vec{v} = a_1 \vec{v}_1 + \cdots + a_m \vec{v}_m \quad \forall \ v \in V $$

Autrement dit, les combinaisons linéaires des vecteurs de $S$ engendrent l’ensemble de l’espace $V$.

Les vecteurs de $S$ sont donc appelés générateurs.

Ainsi, si l’on prend un ensemble $S$ de vecteurs dans $V$ :

$$ S = \{ v_1, v_2, \dots, v_n \} $$

Le plus petit sous-espace vectoriel contenant $S$ est exactement $V$ :

$$ L(S) = V $$

Le nombre de générateurs peut être fini ou infini, mais ne doit pas excéder la quantité nécessaire pour décrire complètement l’espace :

$$ m \le i $$

Dans ce qui suit, $S$ désigne l’ensemble générateur et $L(S)$ le sous-espace qu’il engendre.

Rôle d’un système générateur

Un espace vectoriel $V$ peut contenir une infinité de vecteurs, mais il n’est pas nécessaire de tous les répertorier pour le caractériser.

En effet, tout vecteur $v \in V$ peut s’obtenir comme combinaison linéaire d’un sous-ensemble adéquat de vecteurs de $V$.

Exemple

$$ v_4 = a_1 v_1 + a_2 v_2 + a_3 v_3 \qquad v_5 = a_1 v_1 + a_2 v_2 + a_3 v_3 \qquad v_6 = a_1 v_1 + a_2 v_2 + a_3 v_3 \qquad \vdots $$

Il suffit donc de retenir un sous-ensemble fini (ou éventuellement infini) de vecteurs générateurs :

$$ L = \{ v_1, v_2, v_3 \} $$

En combinant linéairement les vecteurs de $S$ avec des scalaires $\alpha_m$, on engendre tout vecteur de $V$ :

$$ \forall \ v \in V \quad v = a_1 v_1 + a_2 v_2 + a_3 v_3 $$

Premier exemple de système générateur

L’espace vectoriel $V = \mathbb{R}^2$ est engendré par seulement deux vecteurs :

$$ v_1 = (1, 0) \qquad v_2 = (0, 1) $$

Dans le plan cartésien $\mathbb{R}^2$, ces vecteurs s’interprètent ainsi :

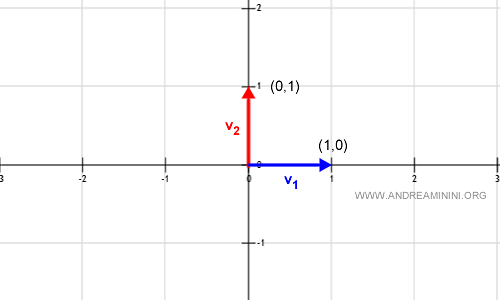
Pour vérifier que $v_1$ et $v_2$ engendrent $\mathbb{R}^2$, considérons la combinaison suivante avec $a_1 = 1$ et $a_2 = 1$ :

$$ v = a_1 v_1 + a_2 v_2 = (1, 0) + (0, 1) = (1, 1) $$

Ce vecteur de coordonnées (1,1) appartient bien à $\mathbb{R}^2$ :

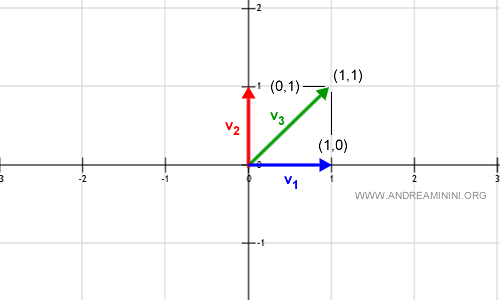
Si l’on prend maintenant $a_2 = 2$ :

$$ v = 1 \cdot (1, 0) + 2 \cdot (0, 1) = (1, 2) $$

On obtient un autre vecteur de $\mathbb{R}^2$, de coordonnées (1,2) :

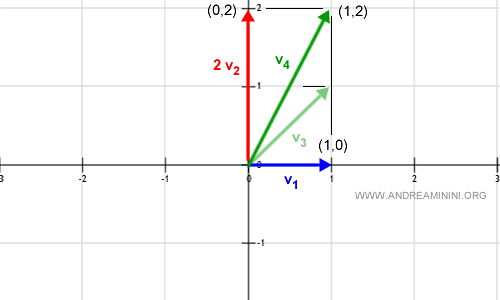
En faisant varier $a_1$ et $a_2$, on engendre ainsi tout vecteur du plan. Par conséquent :

$$ L_{\mathbb{R}} = \{ v_1, v_2 \} = \mathbb{R}^2 $$

Remarque. Un seul vecteur, tel que $v_1$, ne permet pas d’engendrer $\mathbb{R}^2$, puisqu’il ne génère que l’axe $x$. De même, $v_2$ ne génère que l’axe $y$. Pris isolément, chacun définit un sous-espace unidimensionnel.

Exemple 2

Un système générateur peut se réduire à un seul vecteur, à condition que celui-ci ne soit pas nul.

Soit $V$ un espace vectoriel sur le corps $K = \mathbb{R}$, et $\vec{v} \in V$ un vecteur non nul :

L’ensemble engendré par $v$ s’écrit :

$$ L(v) = \{ k \cdot \vec{v} \mid k \in K \} $$

Les vecteurs ainsi obtenus ont tous la même direction et forment une droite :

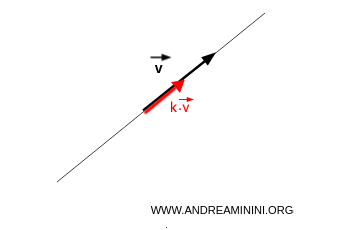
Seules leur norme et leur orientation varient.

Remarque. Le vecteur générateur doit être non nul, car multiplier le vecteur nul par n’importe quel scalaire donne toujours le vecteur nul.

Exemple 3

En général, deux vecteurs non nuls engendrent un sous-espace dont la nature dépend de leur indépendance linéaire :

$$ \vec{v}_1 \ne \vec{0} \qquad \vec{v}_2 \ne \vec{0} $$

• Si les vecteurs sont parallèles $$ \vec{v}_1 = k \cdot \vec{v}_2 $$ Le sous-espace $L(v_1, v_2)$ est alors une droite :
  
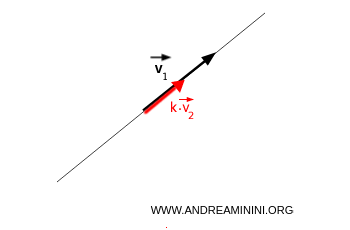
• Si les vecteurs ne sont pas parallèles $$ \vec{v}_1 \ne k \cdot \vec{v}_2 $$ Le sous-espace engendré par $v_1$ et $v_2$ est le plan qu’ils définissent ensemble :
  

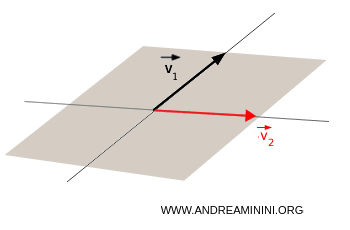
Déterminer si un ensemble de vecteurs est générateur

Pour savoir si un ensemble de vecteurs engendre un espace vectoriel $V$, il suffit de vérifier que toute combinaison linéaire de ses éléments permet de représenter un vecteur arbitraire de $V$. Pour cela, on établit le système d’équations correspondant.

Exemple pratique

Considérons les vecteurs $v_1 = (1,1)$ et $v_2 = (2,1)$ dans l’espace $V = \mathbb{R}^2$.

Nous cherchons à déterminer si ces vecteurs engendrent tout le plan $\mathbb{R}^2$.

Formons la combinaison linéaire :

$$ a_1 v_1 + a_2 v_2 = a_1 (1,1) + a_2 (2,1) = (a_1 + 2a_2,\ a_1 + a_2) $$

Elle doit être égale à un vecteur générique $(x, y) \in \mathbb{R}^2$, ce qui conduit au système :

$$ \begin{cases} a_1 + 2a_2 = x \\ a_1 + a_2 = y \end{cases} $$

Si ce système admet une solution pour tout $(x, y)$, alors $v_1$ et $v_2$ engendrent $\mathbb{R}^2$.

Remarque. Selon le théorème de Rouché-Capelli, un système linéaire admet une solution si le rang de la matrice des coefficients coïncide avec celui de la matrice augmentée. Dans ce cas, le système est compatible (déterminé ou indéterminé).

Ici, le système est toujours soluble. Par conséquent, $v_1$ et $v_2$ engendrent bien $\mathbb{R}^2$.

Vérification algébrique

En résolvant le système :

$$ a_1 = y - a_2 \Rightarrow x = a_1 + 2a_2 = y - a_2 + 2a_2 = y + a_2 \Rightarrow a_2 = x - y $$

Puis :

$$ a_1 = y - (x - y) = 2y - x $$

Quel que soit le couple $(x, y)$, on peut donc trouver des $a_1$ et $a_2$ tels que $a_1 v_1 + a_2 v_2 = (x, y)$, ce qui confirme que $\{v_1, v_2\}$ constitue bien un système générateur de $\mathbb{R}^2$.

Différence entre span linéaire et ensemble générateur

Le span linéaire d’un ensemble $S_p = \{ v_1, v_2, \dots, v_m \}$ est l’ensemble de toutes les combinaisons linéaires possibles de ses vecteurs :

$$ L(S_p) = \left\{ a_1 v_1 + \cdots + a_m v_m \;\middle|\; a_i \in \mathbb{R} \right\} $$

Cet ensemble est toujours un sous-espace de $V$ :

$$ L(S_p) \subseteq V $$

mais il ne coïncide pas nécessairement avec $V$ tout entier :

$$ L(S_p) \ne V $$

Remarque. Les vecteurs de $S_p$ engendrent uniquement le sous-espace $L(S_p)$. Ce n’est que lorsque $L(S_p) = V$ que l’on dit que $S_p$ est un ensemble générateur de $V$.

Ainsi, tout ensemble générateur définit un span, mais tout span n’est pas nécessairement générateur de l’espace complet :

$$ L(S_p) \ne L(S) = V $$

Réduction d’un ensemble générateur

Un ensemble $\{v_1, \dots, v_m\}$ peut engendrer $V$, sans pour autant être minimal. Il peut contenir des vecteurs redondants, qui n’apportent aucune nouvelle direction.

Par exemple, si l’on ajoute un vecteur $v_{m+1}$ tel que $a_{m+1} = 0$ dans toutes les combinaisons, l’ensemble reste générateur :

$$ v = a_1 v_1 + \cdots + a_m v_m + 0 \cdot v_{m+1} $$

Exemple

Comment simplifier un ensemble générateur ?

Il faut éliminer les vecteurs linéairement dépendants, c’est-à-dire ceux qui peuvent s’exprimer comme combinaison linéaire des autres.

Démonstration

Supposons que $v_m$ dépende linéairement de $v_1, \dots, v_{m-1}$ :

$$ v_m = \beta_1 v_1 + \cdots + \beta_{m-1} v_{m-1} $$

Alors toute combinaison :

$$ v = a_1 v_1 + \cdots + a_m v_m $$

peut se réécrire ainsi :

$$ v = a_1 v_1 + \cdots + a_m (\beta_1 v_1 + \cdots + \beta_{m-1} v_{m-1}) $$

$$ = \gamma_1 v_1 + \cdots + \gamma_{m-1} v_{m-1} $$

où les coefficients $\gamma_i = a_i + a_m \beta_i$ appartiennent toujours à $\mathbb{R}$.

On en conclut que $\{v_1, \dots, v_{m-1}\}$ engendre également $V$.

Exemple

Différence entre ensemble générateur et base

Un ensemble générateur devient une base de l’espace vectoriel $V$ si, en plus, ses vecteurs sont linéairement indépendants :

$$ S = \{ v_1, v_2, \dots, v_n \} $$

On appelle aussi une base un système générateur libre.

Dans ce cas, chaque vecteur de $V$ s’écrit de manière unique comme combinaison linéaire des vecteurs de $S$ :

$$ \vec{v} = a_1 v_1 + \cdots + a_n v_n \quad \text{de façon unique} $$

Remarque. Si les vecteurs du système générateur sont linéairement dépendants, alors chaque vecteur de $V$ peut s’exprimer de plusieurs façons différentes, et l’ensemble n’est pas une base.