Exercice 3: Sous-espace vectoriel
Soit $V = \mathbb{R}^2$ et considérons le sous-ensemble : $$ W = \{ (x, y) \in \mathbb{R}^2 \mid x^2 - y = 0 \} $$ On cherche à déterminer si $W$ est un sous-espace vectoriel de $V$.
Pour qu’un tel ensemble soit un sous-espace, il doit vérifier l’ensemble des axiomes d’un espace vectoriel : contenir le vecteur nul, être stable par addition et par multiplication par un scalaire.
1) Vérification du vecteur nul
Soit $\vec{w} = \begin{pmatrix} x \\ y \end{pmatrix}$ un vecteur quelconque de $W$. Par définition :
$$ \vec{w} \in W \quad \Leftrightarrow \quad x^2 - y = 0 $$
Vérifions si le vecteur nul $\begin{pmatrix} 0 \\ 0 \end{pmatrix}$ appartient à $W$ :
$$ 0^2 - 0 = 0 $$
La condition est bien remplie : le vecteur nul appartient donc à $W$.
Remarque. La présence du vecteur nul constitue une condition préalable indispensable. Si un ensemble ne contient pas ce vecteur, il ne peut en aucun cas être considéré comme un sous-espace.
2) Stabilité par addition de vecteurs
Examinons maintenant la stabilité par addition. Prenons deux vecteurs de $W$ :
$$ \vec{w}_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}, \quad \text{où } x_1^2 - y_1 = 0 $$
$$ \vec{w}_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}, \quad \text{où } x_2^2 - y_2 = 0 $$
La somme de ces vecteurs est :
$$ \vec{w}_1 + \vec{w}_2 = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \end{pmatrix} $$
Vérifions si ce vecteur satisfait encore la condition $x^2 - y = 0$ :
$$ (x_1 + x_2)^2 - (y_1 + y_2) = x_1^2 + 2x_1x_2 + x_2^2 - y_1 - y_2 $$
En regroupant les termes :
$$ = (x_1^2 - y_1) + (x_2^2 - y_2) + 2x_1x_2 $$
Puisque $x_1^2 - y_1 = 0$ et $x_2^2 - y_2 = 0$, il reste :
$$ 0 + 0 + 2x_1x_2 = 2x_1x_2 $$
Cette expression n’est nulle que si $x_1 = 0$ ou $x_2 = 0$, mais pas en général.
Donc, en général, la somme $\vec{w}_1 + \vec{w}_2$ n’appartient pas à $W$ :
$$ \vec{w}_1 + \vec{w}_2 \notin W $$
Il s’ensuit que $W$ n’est pas stable par addition vectorielle, ce qui contredit l’une des conditions essentielles pour être un sous-espace.
On conclut donc que $W$ n’est pas un sous-espace vectoriel de $\mathbb{R}^2$.
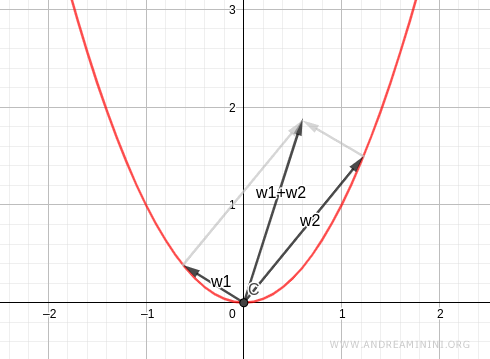
Remarque. Géométriquement, l’équation $x^2 - y = 0$ représente une parabole, et non une droite. Or la somme de deux vecteurs situés sur une parabole ne reste pas, en général, sur celle-ci.
Et l’on poursuit de la même manière pour les exercices suivants.