Sous-espace vectoriel engendré par un ensemble de vecteurs

Le sous-espace vectoriel engendré par un ensemble S de vecteurs d’un espace vectoriel V $$ S = \{ v_1 , v_2, ... , v_n \} $$ est le plus petit sous-espace de V contenant tous les vecteurs de S. On le note L(S) ou <S> : $$ L(S) \ \ \ ou \ \ \ <S> $$ La lettre L renvoie à « linéaire ».

L’ensemble S, pris isolément, n’est pas un sous-espace vectoriel.

$$ S = \{ v_1 , v_2, ... , v_n \} $$

Le sous-espace L(S) est constitué de toutes les combinaisons linéaires possibles des vecteurs de S :

$$ L(S) = \{ \lambda_1 v_1 + \lambda_2 v_2 + ... + \lambda_n v_n \ | \ v_i \in S, \ \lambda_i \in K \} $$

Explication

Considérons un espace vectoriel V.

Soit S un ensemble de vecteurs appartenant à V :

$$ S = \{ v_1 , v_2, ... , v_n \} \subset V $$

En général, S n’est pas un sous-espace : ce n’est qu’un ensemble de deux ou plusieurs vecteurs.

Le plus petit sous-espace de V contenant S s’appelle le sous-espace engendré par S, et se note L(S) ou <S> :

$$ L(S) \ \ \ ou \ \ \ <S> $$

Ce sous-espace est obtenu en considérant toutes les combinaisons linéaires des n vecteurs de S avec des scalaires du corps K :

$$ L(S) = \{ k_1 \vec{v}_1 + k_2 \vec{v}_2 + ... + k_n \vec{v}_n \ \ | \ \vec{v}_i \in S, \ k_i \in K \} $$

On peut aussi écrire cette définition sous forme sommatoire :

$$ L(S) = \left\{ \sum_{i=1}^n k_i \vec{v}_i \ \bigg| \ \vec{v}_i \in S \right\} $$

Le sous-espace L(S) contient en général une infinité de vecteurs ($m \ge n$), tous issus des combinaisons linéaires des n vecteurs de départ.

Sous-espace engendré par un seul vecteur

Considérons un vecteur non nul de V :

$$ \vec{v} \in V \ , \ \vec{v} \ne 0 $$

Dans ce cas, l’ensemble S se réduit à ce seul vecteur :

$$ S = \{ \vec{v} \} \subset V $$

D’un point de vue géométrique, ce vecteur définit une droite passant par l’origine.

Le sous-espace engendré par S est alors formé de tous les multiples scalaires de ce vecteur :

$$ L(\vec{v}) = \{ \lambda \vec{v} \ | \ \lambda \in K \} $$

Ce sous-espace regroupe tous les vecteurs portés par la même droite.

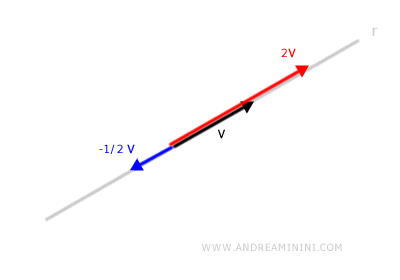
Tous ces vecteurs partagent la même direction, mais peuvent différer en norme et en sens.

Remarque. Dans le cas particulier où le vecteur est nul, le sous-espace engendré se réduit au seul vecteur nul : $$ L(\vec{0}) = \{ \vec{0} \} $$ en effet, tout scalaire multiplié par le vecteur nul reste le vecteur nul.

Sous-espace engendré par deux vecteurs

Le sous-espace engendré par deux vecteurs non nuls $\vec{v}_1$ et $\vec{v}_2$ dans un espace vectoriel $V$ défini sur un corps $K$

$$ v_1, v_2 \in V \ , \ v_1,v_2 \ne \vec{0} $$

dépend de leur dépendance ou indépendance linéaire.

• Si les deux vecteurs sont parallèles
  Ils sont alors linéairement dépendants : l’un peut s’écrire comme un multiple scalaire de l’autre. $$ \vec{v}_1 = \lambda \cdot \vec{v}_2 \ \ \lambda \in K $$ Ils ont donc la même direction et appartiennent à une même droite.
  
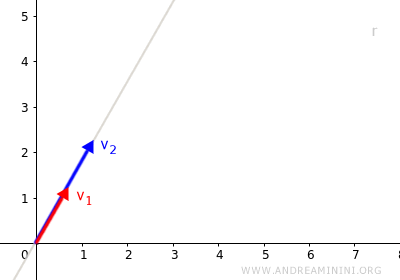
  En conséquence, toutes leurs combinaisons linéaires restent sur cette droite : $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \lambda_1, \lambda_2 \in K \} $$
• Si les deux vecteurs ne sont pas parallèles
  Ils sont alors linéairement indépendants : aucun ne peut s’écrire comme un multiple de l’autre. $$ \vec{v}_1 \ne \lambda \cdot \vec{v}_2 \ \ \lambda \in K $$ Ils possèdent donc des directions distinctes et déterminent un plan.
  
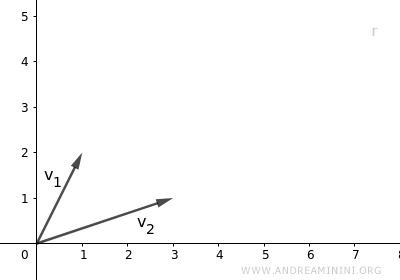
  Leurs combinaisons linéaires engendrent alors tous les vecteurs du plan défini par $\vec{v}_1$ et $\vec{v}_2$ : $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \lambda_1, \lambda_2 \in K \} $$

Exemple

Considérons l’ensemble de vecteurs suivant :

$$ S = \{ \vec{v}_1, \vec{v}_2 \} $$

avec :

$$ \vec{v}_1 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ \vec{v}_2 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

D’un point de vue géométrique, ces vecteurs ne sont pas parallèles : ils sont donc linéairement indépendants.

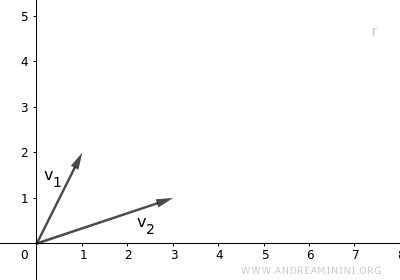
Cet ensemble appartient à l’espace vectoriel $V = \mathbb{R}^2$ :

$$ S \subset V = \mathbb{R}^2 $$

Le sous-espace engendré par $S$ est le plan constitué de toutes les combinaisons linéaires de $\vec{v}_1$ et $\vec{v}_2$ :

$$ L(S) = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$

$$ L(S) = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

où $\lambda_1$ et $\lambda_2$ sont des scalaires réels arbitraires.

Ce sous-espace regroupe donc tous les vecteurs obtenus par combinaisons linéaires de $\vec{v}_1$ et $\vec{v}_2$.

Remarque. En prenant $\lambda_1 = 2$ et $\lambda_2 = 3$, on obtient le vecteur suivant : $$ \vec{v}_n = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$ $$ \vec{v}_n = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + 3 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 9 \\ 3 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 11 \\ 7 \end{pmatrix} $$ Géométriquement :

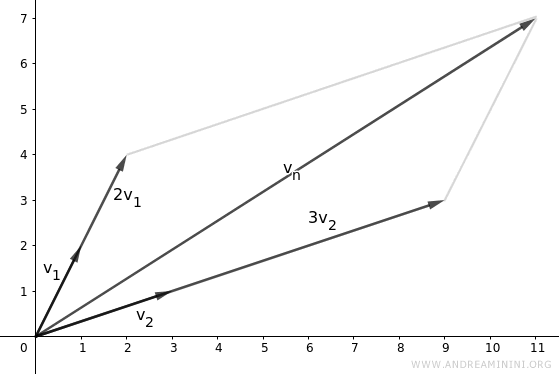
Et ainsi de suite.