Intersection de sous-espaces vectoriels

L’intersection de deux sous-espaces vectoriels est elle-même un sous-espace vectoriel.

Soit V un espace vectoriel sur un corps K, et soient A et B deux de ses sous-espaces. Alors, leur intersection A∩B est également un sous-espace de V.

Démonstration

Considérons un espace vectoriel V et deux de ses sous-espaces, A et B.

Nous voulons montrer que l’intersection A∩B est un sous-espace vectoriel.

Pour cela, il suffit de vérifier qu’elle satisfait les axiomes définissant un sous-espace.

Remarque : Un sous-espace vectoriel doit contenir le vecteur nul et être fermé à la fois pour l’addition de vecteurs et pour la multiplication par un scalaire.

1) Contention du vecteur nul

Comme A et B sont des sous-espaces, ils contiennent nécessairement le vecteur nul.

$$ \vec{0} \in A \qquad \vec{0} \in B $$

On en déduit que le vecteur nul appartient aussi à leur intersection :

$$ \vec{0} \in A∩B $$

L’intersection satisfait donc la première condition pour être un sous-espace vectoriel.

2) Fermeture par addition de vecteurs

Soient deux vecteurs quelconques de l’intersection :

$$ \vec{a}, \vec{b} \in A∩B $$

Autrement dit, ils appartiennent simultanément à A et à B :

$$ \vec{a}, \vec{b} \in A \qquad \vec{a}, \vec{b} \in B $$

Puisque A et B sont fermés pour l’addition, on a :

$$ \vec{a} + \vec{b} \in A \qquad \vec{a} + \vec{b} \in B $$

Donc, la somme appartient elle aussi à l’intersection :

$$ \vec{a} + \vec{b} \in A∩B $$

On a ainsi établi que l’intersection A∩B est fermée pour l’addition vectorielle.

3) Fermeture par multiplication scalaire

Soit $\vec{v} \in A∩B$ un vecteur quelconque, et soit $\lambda \in K$ un scalaire.

Comme $\vec{v}$ appartient à la fois à A et à B, qui sont fermés pour la multiplication scalaire, on obtient :

$$ \lambda \cdot \vec{v} \in A \qquad \lambda \cdot \vec{v} \in B $$

Donc :

$$ \lambda \cdot \vec{v} \in A∩B $$

On a montré que l’intersection A∩B est fermée pour la multiplication par un scalaire.

Conclusion

L’intersection de deux sous-espaces contient le vecteur nul et vérifie les propriétés de fermeture pour l’addition et la multiplication scalaire. Ainsi, A∩B est bien un sous-espace vectoriel.

En outre, A∩B est un sous-espace de A, de B, et de l’espace vectoriel V auquel A et B appartiennent.

Un exemple concret

Le plan cartésien xy peut être vu comme un espace vectoriel V sur le corps K = ℝ².

Il s’agit d’un plan bidimensionnel, ℝ×ℝ.

Les axes de coordonnées X et Y constituent des sous-espaces vectoriels de l’espace V.

Ce sont deux systèmes linéaires homogènes qui contiennent le vecteur nul.

$$ X = \left\{ \binom{x}{y} \in ℝ^2 \mid y = 0 \right\} $$

$$ Y = \left\{ \binom{x}{y} \in ℝ^2 \mid x = 0 \right\} $$

L’intersection des axes X⋂Y se définit ainsi :

$$ X \cap Y = \left\{ \binom{x}{y} \in ℝ^2 \mid x = 0, \ y = 0 \right\} $$

En pratique, cette intersection contient uniquement le vecteur nul.

$$ X \cap Y = \left\{ \vec{0} \right\} $$

Remarque. Cela ne signifie pas que l’intersection soit vide : $$ X \cap Y \ne \Oslash $$. Elle contient bien au moins un élément, le vecteur nul.

D’un point de vue graphique, l’intersection correspond à l’origine O (en bleu) du système cartésien.

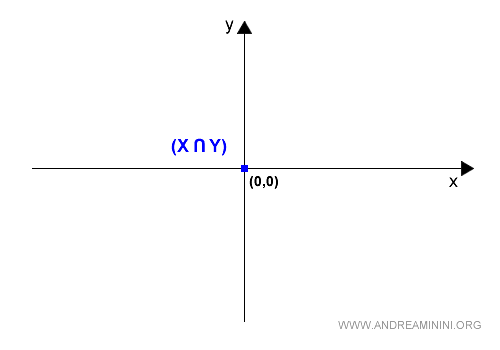
La seule présence du vecteur nul ne suffit pas à garantir que X⋂Y soit un sous-espace vectoriel.

Il faut également vérifier que les autres propriétés essentielles soient respectées.

Propriété 1 (fermeture pour l’addition de vecteurs)

Soient deux vecteurs quelconques de l’intersection X⋂Y :

$$ \vec{x} \in X \cap Y \qquad \vec{y} \in X \cap Y $$

Puisque X⋂Y ne contient que le vecteur nul, on a :

$$ \vec{x} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \qquad \vec{y} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

La somme de deux vecteurs nuls est encore le vecteur nul :

$$ \vec{x} + \vec{y} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Donc, la somme appartient à l’intersection :

$$ \vec{x} + \vec{y} \in X \cap Y $$

Il est donc vérifié que X⋂Y est fermé pour l’addition vectorielle.

Propriété 2 (fermeture pour la multiplication scalaire)

Soit $k \in ℝ$ un scalaire, et $\vec{x} \in X \cap Y$ un vecteur de l’intersection.

Comme $\vec{x}$ est nécessairement le vecteur nul :

$$ \vec{x} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Le produit d’un scalaire par le vecteur nul est encore le vecteur nul :

$$ k \cdot \vec{0} = k \cdot \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Ainsi, le produit appartient lui aussi à l’intersection :

$$ k \cdot \vec{0} \in X \cap Y $$

La seconde propriété caractéristique des sous-espaces est donc respectée.

Conclusion

L’intersection des axes X et Y vérifie les conditions requises : elle contient le vecteur nul, elle est fermée pour l’addition et pour la multiplication scalaire. C’est donc bien un sous-espace vectoriel.

Par conséquent, X⋂Y est un sous-espace de X, de Y, ainsi que de l’espace vectoriel V (le plan cartésien).

Remarques

Quelques remarques importantes concernant l’intersection de sous-espaces vectoriels :

• L’intersection de deux sous-espaces vectoriels n’est jamais vide

  Démonstration. Comme X et Y sont des sous-espaces, ils contiennent tous deux par définition le vecteur nul : $$ \vec{0} \in X \ , \ \vec{0} \in Y \ \Rightarrow\ \vec{0} \in X \cap Y $$ Leur intersection contient donc au moins un élément et ne peut pas être vide. Il se peut qu’elle ne contienne que le vecteur nul : $$ X \cap Y = \left\{ \vec{0} \right\} $$ mais on n’a jamais : $$ X \cap Y = \Oslash $$