Somme directe de sous-espaces vectoriels

La somme de deux sous-espaces $A$ et $B$ est dite somme directe lorsque leur intersection se réduit au seul vecteur nul.

Soit $V$ un espace vectoriel sur un corps $K$, et $A$, $B$ deux sous-espaces de $V$. Leur somme est dite directe si $$ A \cap B = \{ \vec{0} \} $$. Dans ce cas, on note : $$ A \oplus B $$

La notation $\oplus$ (signe « plus dans un cercle ») indique explicitement qu’il s’agit d’une somme directe, c’est-à-dire d’une intersection triviale.

Exemples

Considérons deux situations permettant de vérifier par un calcul explicite si deux sous-espaces sont en somme directe ou non.

Exemple 1

Dans l’espace vectoriel $V = \mathbb{R}^3$, considérons les sous-espaces :

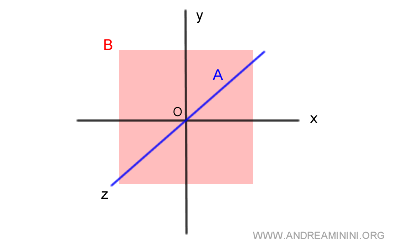
$$ A = \{ (x, y, z) \in \mathbb{R}^3 \mid x = 0, \ y = 0 \} $$

$$ B = \{ (x, y, z) \in \mathbb{R}^3 \mid z = 0 \} $$

Le sous-espace $A$ correspond à l’axe $z$ (en bleu), tandis que $B$ représente le plan $xy$ défini par $z = 0$ (en rouge).

Vérifions leur intersection :

$$ A \cap B = \{ \vec{0} \} $$

C’est bien le cas, puisque le seul vecteur commun aux deux sous-espaces est le vecteur nul (l’origine $O$).

On en conclut que $A$ et $B$ sont en somme directe :

$$ A \oplus B $$

Exemple 2

Dans le même espace $V = \mathbb{R}^3$, considérons maintenant :

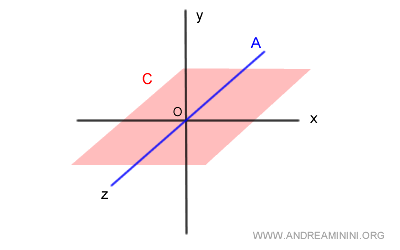
$$ A = \{ (x, y, z) \in \mathbb{R}^3 \mid x = 0, \ y = 0 \} $$

$$ C = \{ (x, y, z) \in \mathbb{R}^3 \mid y = 0 \} $$

Le sous-espace $A$ correspond de nouveau à l’axe $z$ (en bleu), tandis que $C$ est le plan $xz$ défini par $y = 0$ (en rouge).

Examinons leur intersection :

$$ A \cap C = \text{axe } z \ne \{ \vec{0} \} $$

En effet, $A \cap C$ contient l’ensemble des vecteurs de l’axe $z$, c’est-à-dire une infinité d’éléments non nuls.

On en déduit que $A$ et $C$ ne sont pas en somme directe.