Somme de sous-espaces vectoriels
Soit V un espace vectoriel sur un corps K, et soient A et B deux sous-espaces de V. On définit leur somme par : $$ A + B := \{ \vec{a} + \vec{b} \mid \vec{a} \in A, \ \vec{b} \in B \} $$ Cet ensemble est un sous-espace vectoriel qui contient en particulier l’union : $$ A \cup B \subset A + B $$ De plus, A + B est le plus petit sous-espace de V contenant cette union.
On appelle A + B le sous-espace somme.
$$ A + B \subseteq V $$
En particulier : $$ A \subset A + B \qquad B \subset A + B $$
Remarque. L’union A ∪ B n’est en général pas un sous-espace, car elle n’est pas fermée pour l’addition de vecteurs (voir démonstration).
Démonstration
A + B est un sous-espace vectoriel
Comme A et B contiennent le vecteur nul, on a :
$$ \vec{0} = \vec{0} + \vec{0} \in A + B $$
1) Fermeture par addition
Soient $\vec{u}, \vec{w} \in A + B$. Il existe $\vec{a}_1, \vec{a}_2 \in A$ et $\vec{b}_1, \vec{b}_2 \in B$ tels que :
$$ \vec{u} = \vec{a}_1 + \vec{b}_1, \qquad \vec{w} = \vec{a}_2 + \vec{b}_2 $$
Alors :
$$ \vec{u} + \vec{w} = (\vec{a}_1 + \vec{a}_2) + (\vec{b}_1 + \vec{b}_2) $$
Or $\vec{a}_1 + \vec{a}_2 \in A$ et $\vec{b}_1 + \vec{b}_2 \in B$, donc $\vec{u} + \vec{w} \in A + B$.
2) Fermeture par multiplication scalaire
Soit $k \in K$ et $\vec{u} = \vec{a} + \vec{b} \in A + B$ avec $\vec{a} \in A$, $\vec{b} \in B$. Alors :
$$ k\vec{u} = (k\vec{a}) + (k\vec{b}) $$
Comme $k\vec{a} \in A$ et $k\vec{b} \in B$, on a $k\vec{u} \in A + B$.
En conclusion, A + B contient le vecteur nul et est fermé pour l’addition et la multiplication scalaire : c’est donc un sous-espace de V.
A + B contient l’union A ∪ B
Pour tout $\vec{a} \in A$, on a $\vec{a} = \vec{a} + \vec{0} \in A + B$. De même, pour tout $\vec{b} \in B$, $\vec{b} = \vec{0} + \vec{b} \in A + B$. Ainsi : $$ A \cup B \subset A + B $$
Exemple
Dans $V = \mathbb{R}^3$, considérons :
$$ A = \{ \vec{a} \in \mathbb{R}^3 \mid \vec{a} \text{ sur l’axe } x \}, \qquad B = \{ \vec{b} \in \mathbb{R}^3 \mid \vec{b} \text{ sur l’axe } y \} $$
A est l’ensemble des vecteurs de l’axe X, B celui de l’axe Y.
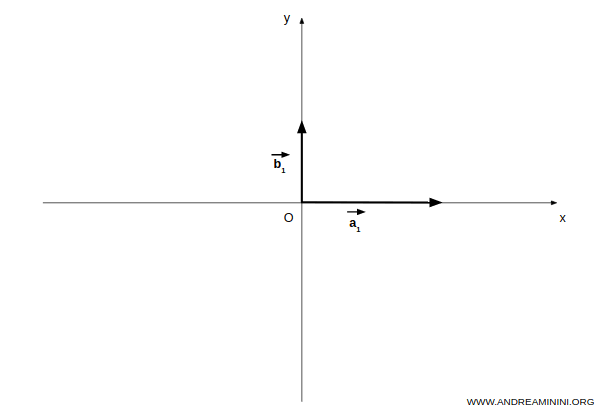
Leur somme $A + B$ contient tous les vecteurs de A, de B, ainsi que leurs combinaisons linéaires : c’est le plan XY.
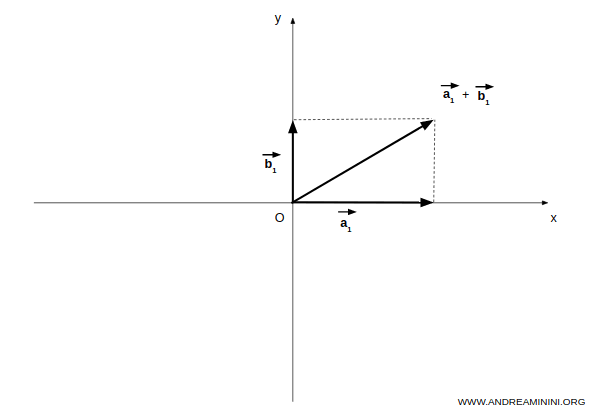
Le plus petit sous-espace contenant A et B
La somme $A + B$ est le plus petit sous-espace de $V$ contenant $A \cup B$.
Démonstration
Soit $L$ un sous-espace de $V$ tel que $A \cup B \subseteq L$. Comme $L$ est fermé pour l’addition, on a :
$$ \{ \vec{a} + \vec{b} \mid \vec{a} \in A, \ \vec{b} \in B \} \subseteq L $$
donc $A + B \subseteq L$.
Tout sous-espace contenant A et B contient donc leur somme. Comme $A + B$ est lui-même un sous-espace, il est minimal avec cette propriété.
Remarque. Aucun ensemble strictement intermédiaire $Z$ tel que $A, B \subset Z \subset A + B$ ne peut être un sous-espace, car il ne serait pas fermé pour l’addition.