Exercices sur les espaces vectoriels
Voici quelques exemples entièrement résolus illustrant les notions fondamentales relatives aux espaces vectoriels.
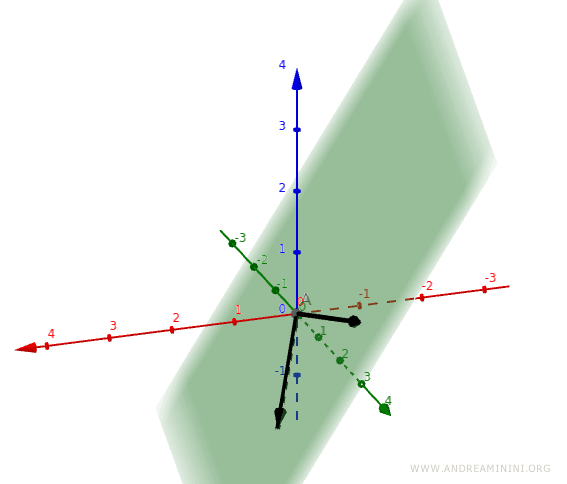
Exercice 1
Considérons les deux vecteurs suivants dans l’espace vectoriel $V = \mathbb{R}^3$ :
$$ \vec{v}_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}, \quad \vec{v}_2 = \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$
Ces deux vecteurs engendrent-ils $\mathbb{R}^3$ ?
Pour le déterminer, examinons si un vecteur arbitraire $\vec{v} \in \mathbb{R}^3$ :
$$ \vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} \in V = \mathbb{R}^3 $$
peut s’exprimer comme une combinaison linéaire de $\vec{v}_1$ et $\vec{v}_2$ :
$$ \vec{v} = \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 $$
$$ \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \lambda_1 \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \lambda_2 \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$
Ce qui conduit au système suivant :
$$ \begin{cases} \lambda_1 = a \\ 2\lambda_1 + 3\lambda_2 = b \\ -\lambda_1 + \lambda_2 = c \end{cases} $$
En remplaçant $\lambda_1 = a$ dans les deux dernières équations, on obtient :
$$ \begin{cases} \lambda_1 = a \\ 2a + 3\lambda_2 = b \\ \lambda_2 = c + a \end{cases} $$
Substituons $\lambda_2 = c + a$ dans la deuxième équation :
$$ 2a + 3(c + a) = b $$
soit :
$$ 5a + 3c = b $$
Cette relation montre que le système n’admet de solution que si $a$, $b$ et $c$ satisfont cette condition. Autrement dit, le système n’est pas résoluble pour des valeurs arbitraires de $(a, b, c)$.
Conclusion : les vecteurs $\vec{v}_1$ et $\vec{v}_2$ n’engendrent pas l’espace entier $\mathbb{R}^3$.
Remarque. En général, deux vecteurs linéairement indépendants engendrent au maximum un plan ($\mathbb{R}^2$) dans l’espace. Puisque $\mathbb{R}^3$ est de dimension trois, il faut au moins trois vecteurs linéairement indépendants pour en engendrer tout l’espace.
Exercice 2
Considérons l’espace vectoriel $M(2,2,\mathbb{R})$, c’est-à-dire l’ensemble de toutes les matrices réelles $2 \times 2$. On définit le sous-ensemble $A$ de $M(2,2,\mathbb{R})$ par :
$$ A = \left\{ \begin{pmatrix} a & b \\ c & 1 \end{pmatrix} \ \middle| \ a,b,c \in \mathbb{R} \right\} $$
$A$ est-il un sous-espace vectoriel de $M(2,2,\mathbb{R})$ ?
Pour le déterminer, vérifions si $A$ satisfait à tous les axiomes d’un espace vectoriel et aux conditions nécessaires à l’existence d’un sous-espace.
1] $A$ est-il un espace vectoriel ?
L’ensemble $A$ est non vide, mais il est immédiat de constater que la matrice nulle :
$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \notin A $$
n’appartient pas à $A$, car dans toute matrice de $A$, le coefficient en position $(2,2)$ est fixé à $1$. Or, la présence de la matrice nulle est une condition indispensable pour qu’un ensemble soit un espace vectoriel.
Par conséquent, $A$ n’est pas un espace vectoriel, et donc $A$ n’est pas un sous-espace de $M(2,2,\mathbb{R})$.
Remarque. Cet exemple illustre l’importance de vérifier en premier lieu les conditions les plus élémentaires - comme la présence de l’élément neutre - avant de passer à des vérifications plus complexes. Cela permet de gagner du temps et d’éviter des calculs inutiles.
Exercice 3
Considérons à nouveau l’espace vectoriel $M(2,2,\mathbb{R})$, l’ensemble de toutes les matrices réelles $2 \times 2$. On définit le sous-ensemble $A$ par :
$$ A = \left\{ \begin{pmatrix} a & b \\ c & b - 1 \end{pmatrix} \ \middle| \ a,b,c \in \mathbb{R} \right\} $$
$A$ est-il un sous-espace vectoriel de $M(2,2,\mathbb{R})$ ?
Pour le savoir, vérifions d’abord si $A$ satisfait les axiomes d’un espace vectoriel, puis s’il répond aux conditions de sous-espace.
1] $A$ est-il un espace vectoriel ?
L’ensemble $A$ est non vide. Cependant, il est évident que la matrice nulle n’appartient pas à $A$ :
$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \notin A $$
En effet, les deux coefficients $b$ et $b - 1$ dépendent du même paramètre $b$, ce qui empêche que les deux soient nuls simultanément :
$$ \begin{pmatrix} a & \color{red}b \\ c & \color{red}{b - 1} \end{pmatrix}, \quad a,b,c \in \mathbb{R} $$
Par exemple, si $a = 0$, $b = 0$ et $c = 0$, on obtient :
$$ \begin{pmatrix} 0 & 0 \\ 0 & \color{red}{-1} \end{pmatrix} $$
Et si $a = 0$, $b = 1$, $c = 0$, on obtient :
$$ \begin{pmatrix} 0 & \color{red}{1} \\ 0 & 0 \end{pmatrix} $$
Dans tous les cas, la matrice nulle ne peut appartenir à $A$. Or, sa présence est indispensable pour que $A$ soit un espace vectoriel.
Nous concluons donc que $A$ n’est pas un espace vectoriel et, par conséquent, $A$ n’est pas un sous-espace de $M(2,2,\mathbb{R})$.
Et ainsi de suite.