Espace vectoriel des vecteurs géométriques appliqués
L’espace vectoriel des vecteurs géométriques appliqués dans un plan, ayant pour origine un point O, est constitué de l’ensemble des vecteurs issus de O et terminant en un point quelconque du plan.
Explication
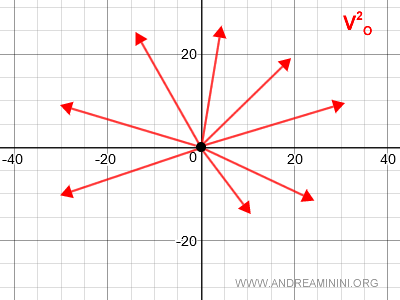
Si l’on fixe un point O dans le plan, l’ensemble de tous les vecteurs ayant O pour origine forme un espace vectoriel noté V2O.
Que désigne un « vecteur appliqué en O » ? C’est un vecteur du type OP, dont l’origine est O et l’extrémité un point P arbitraire du plan.
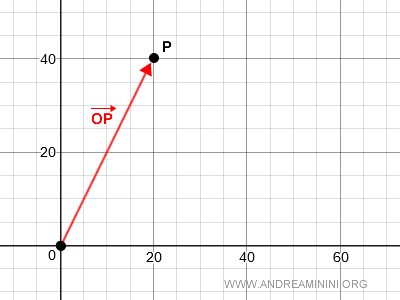
Dans l’espace V2O, on peut effectuer les opérations de base - somme de vecteurs et multiplication par un scalaire - en respectant toutes les propriétés d’un espace vectoriel réel.
Somme de vecteurs
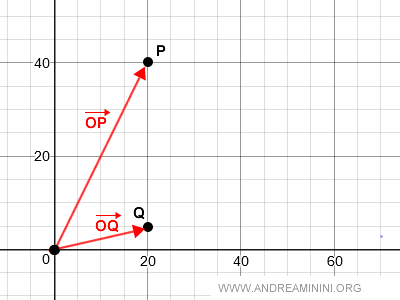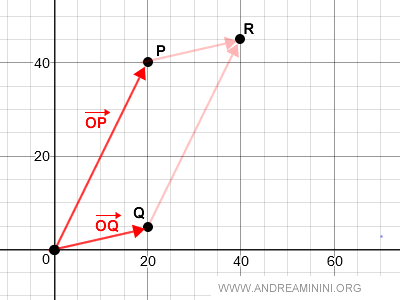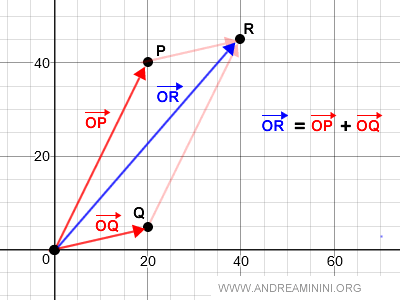
Étant donnés deux vecteurs OP et OQ, leur somme s’obtient en construisant le parallélogramme qu’ils définissent et en prenant pour résultat la diagonale correspondante :
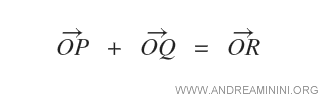
D’après la règle du parallélogramme, le vecteur somme est la diagonale O → R du parallélogramme OPRQ.
Graphiquement, cette opération se représente ainsi :
Produit par un scalaire
Étant donné un vecteur OP et un scalaire α, leur produit est le vecteur OQ, de même origine O, dont l’extrémité Q est telle que la longueur de OQ soit proportionnelle à celle de OP, selon la valeur de α.
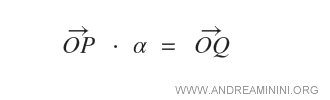
La norme du vecteur OQ est donnée par la relation :
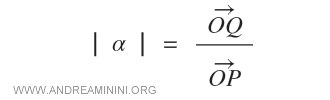
Graphiquement, la multiplication par un scalaire se représente ainsi dans le plan :
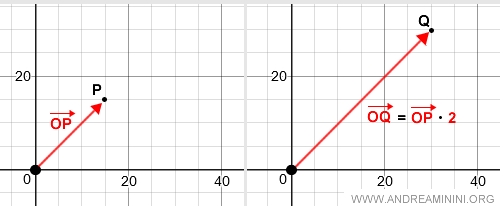
Le signe du scalaire α détermine l’orientation : si α est positif, OQ est dirigé comme OP ; s’il est négatif, OQ est orienté en sens inverse.
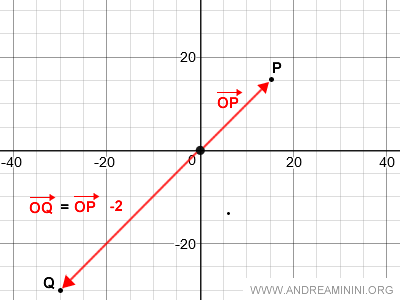
Dans les deux cas, les vecteurs OQ et OP sont colinéaires puisqu’ils appartiennent à la même droite d’action. La valeur absolue de α fixe le rapport entre leurs normes.
Cas particuliers
Si α = 1, le produit ne modifie pas le vecteur : OQ coïncide avec OP.
Si α = -1, on obtient le vecteur opposé : OQ est dirigé à l’opposé de OP et le point Q est le symétrique de P par rapport à O.
Si α = 0, le résultat est le vecteur nul, dont l’origine et l’extrémité se confondent en O : OO.