Multiplication scalaire d’un vecteur

Multiplier un vecteur v par un scalaire k revient à multiplier chacun de ses composants par ce nombre réel. L’opération s’écrit de la manière suivante :

$$ k \cdot \vec{v} = k \cdot \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} k \cdot v_1 \\ k \cdot v_2 \\ \vdots \\ k \cdot v_n \end{pmatrix} $$

Dans ce contexte, un « scalaire » désigne simplement un nombre réel.

La multiplication d’un vecteur v par un scalaire k donne un nouveau vecteur w = k · v qui :

conserve la même direction que v si k est positif,
a une norme égale à |k| fois celle de v,
et s’oriente en sens inverse si k est négatif.

Remarque : si k = 0, on obtient le vecteur nul (le vecteur v est alors « réduit à néant »). Si k = 1, le vecteur reste inchangé ; si k = -1, il est inversé et l’on obtient -v.

Exemple pratique

Considérons un vecteur v dans l’espace à trois dimensions (x, y, z) :

$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

En le multipliant par le scalaire k = 2, on obtient :

$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

Le vecteur résultant est :

$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 6 \\ 2 \\ -4 \end{pmatrix} $$

Exemple 2

Soit un vecteur v de norme |v| = 3 et un scalaire k = 2 :

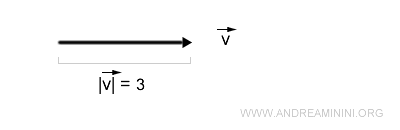
exemple de multiplication scalaire d’un vecteur dans le plan

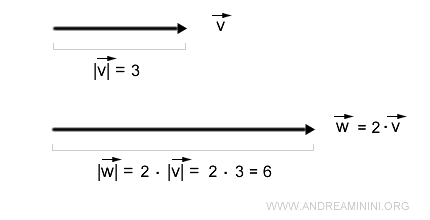
Le vecteur obtenu w garde la même direction que v, mais sa norme devient 6 :

$$ \vec{w} = |k| \cdot \vec{v} $$

$$ | \vec{w} | = |k| \cdot | \vec{v} | = 2 \cdot 3 = 6 $$

Cette relation est illustrée ci-dessous.

illustration graphique de l’augmentation de la norme après multiplication scalaire

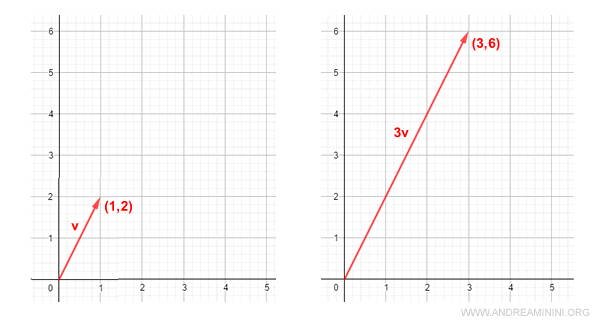
Remarque : multiplier un vecteur par un scalaire k revient à dilater ou contracter chacun de ses composants. Par exemple, si k = 3 et v = (1,2)^T :

$$ k \cdot \vec{v} = 3 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \end{pmatrix} $$

Cette transformation peut également être représentée graphiquement.
visualisation graphique de l’agrandissement d’un vecteur par multiplication scalaire

Exemple 3

Considérons maintenant un vecteur v de norme |v| = 3 et un scalaire négatif k = -2 :

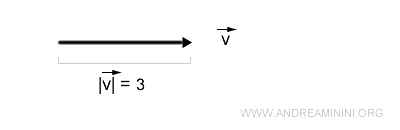
exemple de changement de direction avec multiplication scalaire négative

Le vecteur résultant w est orienté en sens opposé à v et sa norme est 6 :

$$ | \vec{w} | = |k| \cdot | \vec{v} | = |-2| \cdot 3 = 6 $$

Ce renversement de direction, accompagné d’un changement de norme, se visualise ainsi :

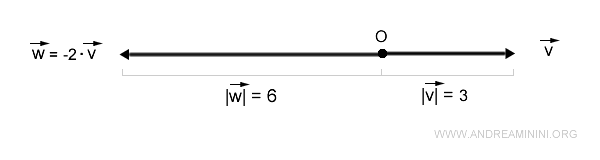
illustration graphique du renversement de direction par multiplication scalaire négative

Remarque : lorsque k = -1, on obtient -v, un vecteur de même norme que v, mais dirigé en sens contraire.