Soustraction de vecteurs
Lorsqu’on travaille avec des vecteurs, il est indispensable de maîtriser la notion de soustraction. Examinons-la en détail.
Soient deux vecteurs \( \vec{v} \) et \( \vec{w} \) ayant le même nombre de composantes. L’opération \( \vec{v} - \vec{w} \) consiste à soustraire, terme à terme, les coordonnées de \( \vec{w} \) de celles de \( \vec{v} \). Formellement : $$ \vec{v} - \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} - \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 - w_1 \\ v_2 - w_2 \\ \vdots \\ v_n - w_n \end{pmatrix} $$ Le vecteur obtenu est appelé le vecteur différence.
Il faut souligner que la soustraction de vecteurs n’est définie que si les deux vecteurs possèdent le même nombre de composantes. Dans le cas contraire, l’opération est impossible.
Exemple
Illustrons cette définition par un exemple concret.
Considérons les vecteurs :
$$ \vec{v} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
Ici, \( \vec{v} \) joue le rôle de minuend et \( \vec{w} \) celui de soustrait.
$$ \vec{v} - \vec{w} $$
En soustrayant les composantes correspondantes, on obtient :
$$ \vec{v} - \vec{w} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 2-4 \\ 5-3 \end{pmatrix} = \begin{pmatrix} -2 \\ 2 \end{pmatrix} $$
Le vecteur obtenu est donc le vecteur différence.
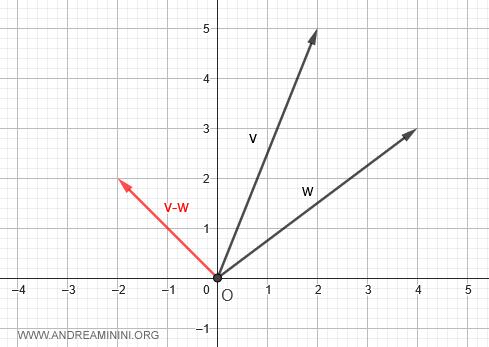
Méthode graphique
Pour une compréhension plus intuitive, il est utile d’envisager la soustraction de vecteurs à l’aide d’une construction graphique.
Reprenons nos deux vecteurs :
$$ \vec{v} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
On les place dans un repère cartésien.
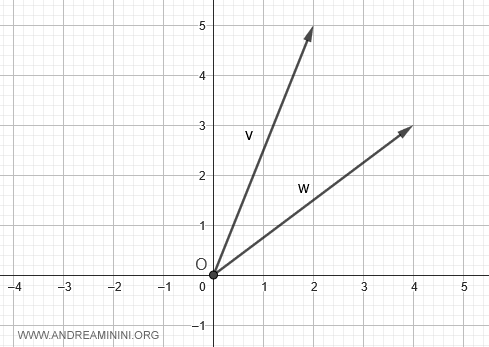
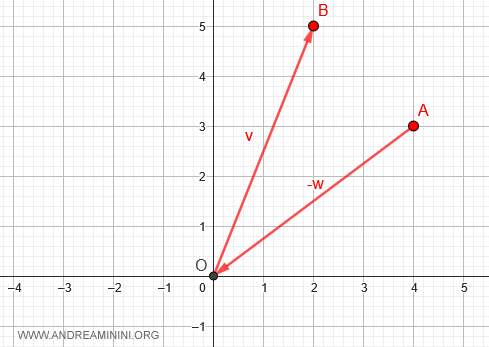
Pour calculer : $$ \vec{v} - \vec{w} $$ on part de l’extrémité du vecteur \( \vec{w} \), c’est-à-dire du point A de coordonnées (4,3).
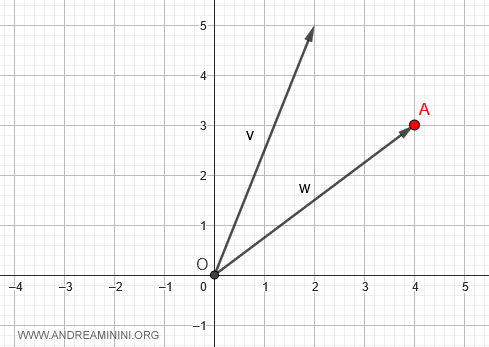
À partir de ce point, on applique le vecteur opposé \(-\vec{w}\), ce qui revient à se déplacer vers l’origine O.
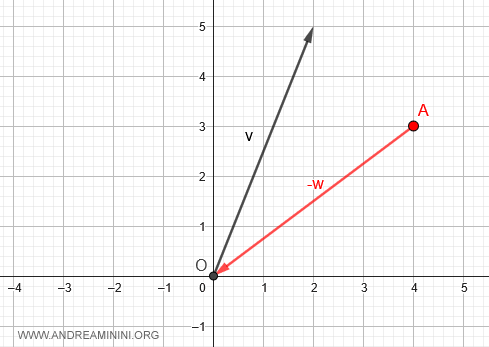
On ajoute ensuite le vecteur \( \vec{v} \), qui nous conduit au point B de coordonnées (2,5).
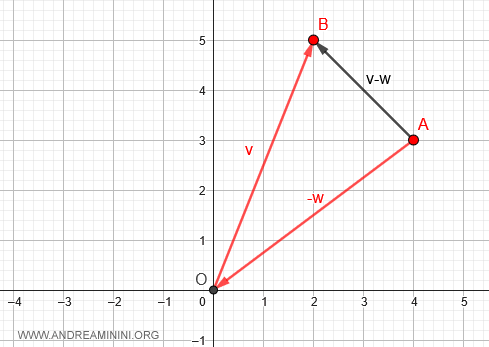
En reliant A et B par un segment orienté, on obtient le vecteur déplacement.
En physique, ce vecteur est appelé vecteur déplacement, car il représente le changement de position entre deux points.
On peut enfin translater ce vecteur de manière à placer son origine en O.
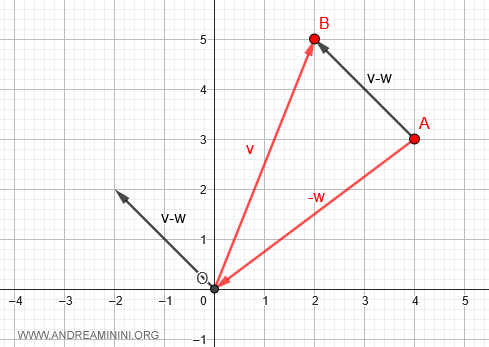
Le vecteur ainsi obtenu représente la différence \( \vec{v} - \vec{w} \).
Cette construction permet de visualiser clairement le sens géométrique de la soustraction de vecteurs.