Angle entre deux vecteurs
Pour calculer l’angle entre deux vecteurs, on utilise une formule reposant sur l’arccosinus. Elle s’appuie sur le rapport entre leur produit scalaire et le produit de leurs normes : $$ \alpha = \arccos \left( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} \right) $$
Cette relation est valable quel que soit le quadrant où se situent les vecteurs.
Elle renvoie toujours l’angle le plus petit entre eux, compris entre 0° et 180°, indépendamment de leur orientation dans le plan.
Exemple
Illustrons la formule par un premier exemple :
Considérons les vecteurs suivants :
$$ \vec{v} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$
Représentés graphiquement, ils apparaissent dans le plan :
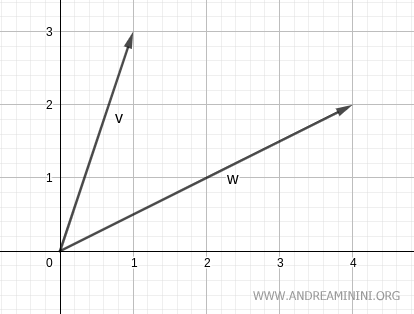
Appliquons la formule de l’angle :
$$ \alpha = \arccos \left( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} \right) $$
Commençons par calculer le produit scalaire :
$$ \vec{v} \cdot \vec{w} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ 2 \end{pmatrix} = 1 \cdot 4 + 3 \cdot 2 = 4 + 6 = 10 $$
En reportant ce résultat dans la formule :
$$ \alpha = \arccos \left( \frac{10}{ |\vec{v}| \cdot |\vec{w}|} \right) $$
Calculons ensuite les normes des vecteurs grâce au théorème de Pythagore :
$$ |\vec{v}| = \sqrt{1^2 + 3^2} = \sqrt{10} $$
$$ |\vec{w}| = \sqrt{4^2 + 2^2} = \sqrt{20} $$
On obtient alors :
$$ \alpha = \arccos \left( \frac{10}{ \sqrt{10} \cdot \sqrt{20} } \right) $$
$$ \alpha = \arccos \left( \frac{10}{ \sqrt{200} } \right) $$
$$ \alpha = \arccos (0,71) $$
Ce qui donne finalement :
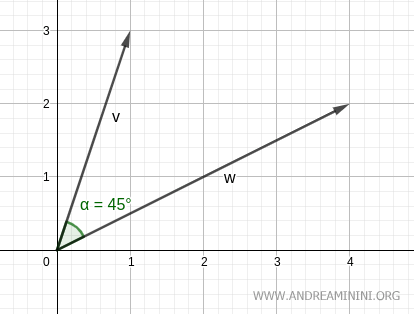
$$ \alpha = 45^\circ $$
L’angle entre ces deux vecteurs est donc de 45°.
Exemple 2
Considérons maintenant deux vecteurs situés dans des quadrants différents :
$$ \vec{v} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} \quad \text{(premier quadrant)} $$
$$ \vec{w} = \begin{pmatrix} -1 \\ 3 \end{pmatrix} \quad \text{(deuxième quadrant)} $$
Leur produit scalaire vaut :
$$ \vec{v} \cdot \vec{w} = 2 \cdot (-1) + 1 \cdot 3 = -2 + 3 = 1 $$
Leurs normes sont :
$$ |\vec{v}| = \sqrt{2^2 + 1^2} = \sqrt{5} $$
$$ |\vec{w}| = \sqrt{(-1)^2 + 3^2} = \sqrt{10} $$
D’où :
$$ \alpha = \arccos \left( \frac{1}{\sqrt{5} \cdot \sqrt{10}} \right) = \arccos \left( \frac{1}{\sqrt{50}} \right) \approx \arccos(0,141) \approx 81,87^\circ $$
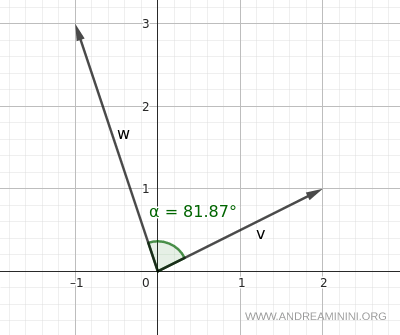
L’angle obtenu est donc d’environ :
$$ \alpha \approx 81,87^\circ $$
Même si les vecteurs appartiennent à des quadrants différents - ce qui influe sur le signe de leurs composantes - la formule fournit toujours correctement l’angle non orienté entre eux, situé entre 0° et 180°. Comme il ne s’agit pas d’un angle orienté, il ne peut en aucun cas être de 270°.
Démonstration
Pour ceux qui souhaitent la justification théorique :
Le produit scalaire de deux vecteurs est égal au produit de leurs normes multiplié par le cosinus de l’angle qui les sépare :
$$ \vec{v} \cdot \vec{w} = |\vec{v}| \cdot |\vec{w}| \cdot \cos \alpha $$
De cette relation, on déduit immédiatement :
$$ \cos \alpha = \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}|} $$
En appliquant l’arccosinus aux deux membres :
$$ \alpha = \arccos \left( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } \right) $$
On confirme ainsi la validité de la formule employée pour déterminer l’angle entre deux vecteurs.