Théorème de Pythagore

Le théorème de Pythagore s’applique aux triangles rectangles, c’est-à-dire à ceux qui comportent un angle droit de 90°. Sa formulation classique s’énonce ainsi :

Dans un triangle rectangle, l’aire du carré construit sur l’hypoténuse (le côté opposé à l’angle droit) est égale à la somme des aires des carrés édifiés sur les deux autres côtés. $$ a^2 + b^2 = c^2 $$ Ici, "c" désigne l’hypoténuse, tandis que "a" et "b" représentent les côtés adjacents à l’angle droit.

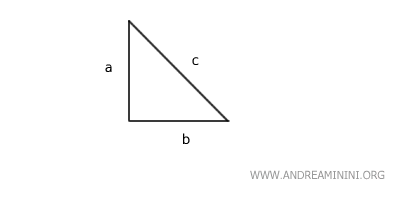
Ce théorème prestigieux doit son nom au mathématicien grec Pythagore, à qui l’on attribue traditionnellement sa première formulation.

Intérêt

Ce résultat permet de calculer la longueur des côtés d’un triangle rectangle.

En connaissant deux côtés, on peut déterminer immédiatement le troisième.

Applications. Le théorème de Pythagore est omniprésent en mathématiques, en géométrie et en physique. Il joue un rôle fondamental dans le calcul des distances et constitue le socle des fonctions trigonométriques : sinus, cosinus et tangente.

Bien qu’énoncé il y a plus de deux mille ans, il reste un pilier de la science moderne et intervient encore dans d’innombrables démonstrations et applications.

Exemple concret

Considérons un triangle rectangle dont les côtés mesurent :

$$ a = 4 \quad b = 3 $$

Nous cherchons à déterminer l’hypoténuse "c".

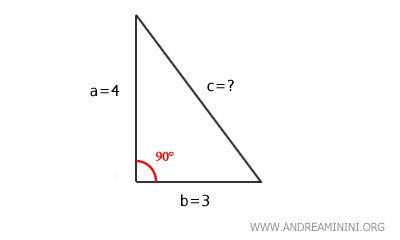
D’après le théorème de Pythagore :

$$ c^2 = a^2 + b^2 $$

En remplaçant par les valeurs numériques :

$$ c^2 = 4^2 + 3^2 = 16 + 9 = 25 $$

En prenant la racine carrée :

$$ c = \sqrt{25} = 5 $$

L’hypoténuse mesure donc 5 unités.

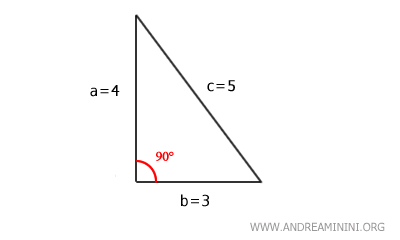
De même, si l’on connaît un côté et l’hypoténuse, on peut retrouver l’autre côté : $$ a^2 = c^2 - b^2 \qquad b^2 = c^2 - a^2 $$. Il suffit d’isoler l’inconnue dans la formule principale $$ c^2 = a^2 + b^2 $$ pour obtenir le résultat recherché.

Démonstrations

On connaît de très nombreuses démonstrations du théorème de Pythagore, certaines datant de l’Antiquité.

L’une des plus élégantes est de nature purement géométrique.

Considérons un triangle rectangle :

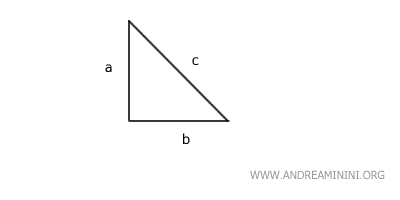
Construisons un carré sur chacun de ses côtés :

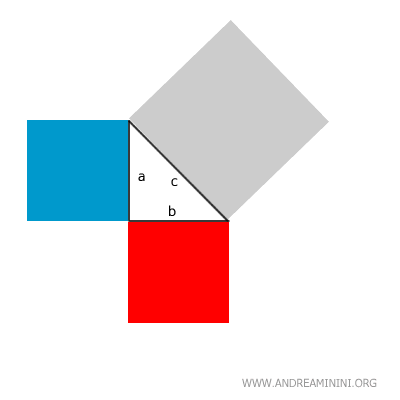
Le plus grand carré (gris) correspond à l’hypoténuse ; les deux autres (rouge et bleu) aux côtés de l’angle droit.

Divisons les petits carrés en triangles rectangles :

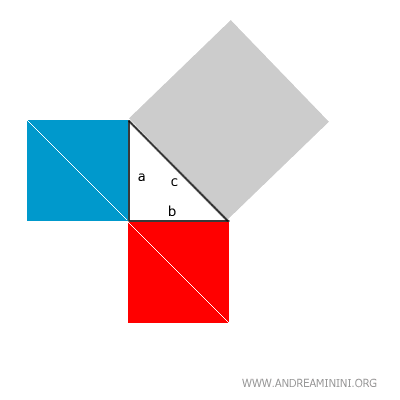
En réassemblant ces pièces, on reconstitue exactement l’aire du grand carré :

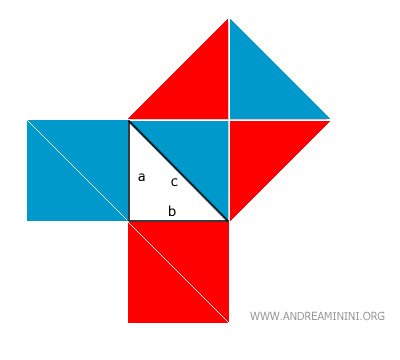
La validité du théorème s’en trouve ainsi mise en évidence de façon visuelle.

Autre démonstration

Une autre preuve classique repose sur un principe d’Euclide.

Construisons des carrés sur chacun des côtés du triangle :

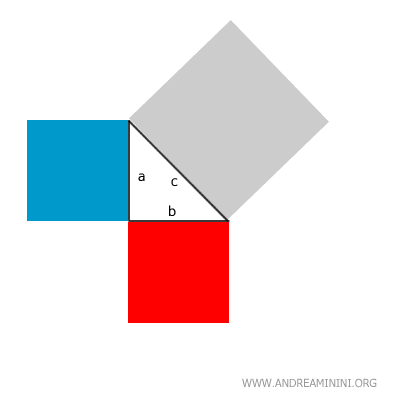
On trace la hauteur (h) issue de l’angle droit vers l’hypoténuse :

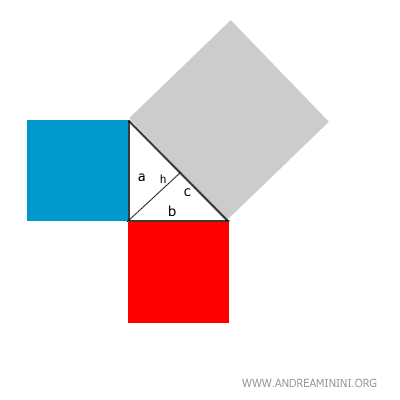
Cette hauteur divise le carré de l’hypoténuse en deux régions (R1 et R2).

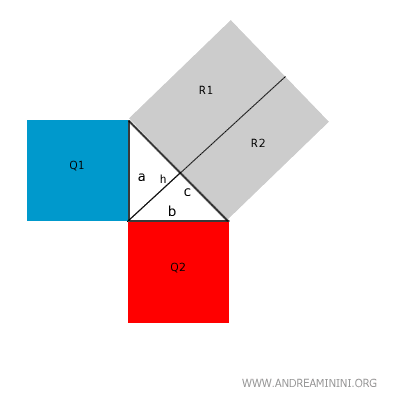
D’après le premier théorème d’Euclide, l’aire du rectangle formé par la projection du côté "a" sur l’hypoténuse est égale au carré de ce côté : Q1 = R1.

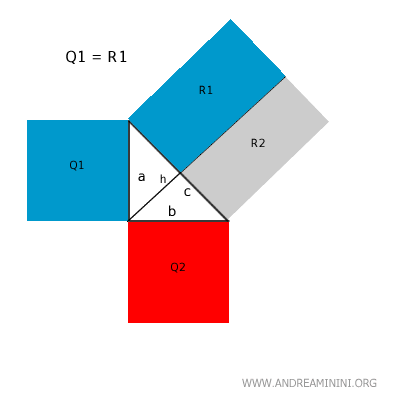
De même, Q2 = R2 pour le côté "b".

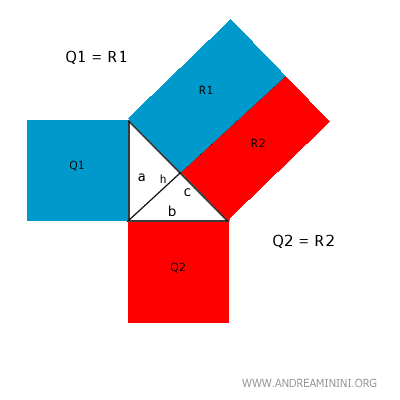
On en déduit donc :

$$ R1 + R2 = Q1 + Q2 $$

ce qui confirme à nouveau le théorème de Pythagore.

Remarque : On connaît des dizaines de démonstrations de ce théorème ; nous n’avons présenté ici que deux des plus classiques.

Observations

• Réciproque du théorème de Pythagore
  

  Si, dans un triangle, la somme des carrés de deux côtés est égale au carré du troisième, alors le triangle est rectangle.

• Théorème de Pythagore généralisé 

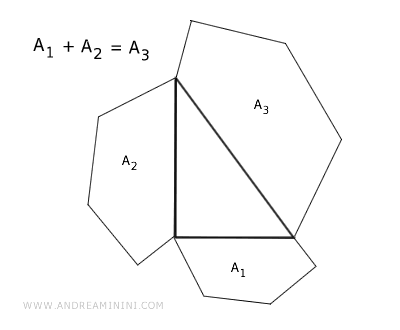
  Dans un triangle rectangle, si l’on construit trois polygones semblables sur ses côtés, l’aire du polygone édifié sur l’hypoténuse (A₃) est égale à la somme des aires des deux autres (A₁ + A₂).
  

• Origine historique
  Selon la tradition, Pythagore aurait eu l’intuition de son théorème en observant le dallage d’un palais à Samos : un carreau brisé en diagonale faisait apparaître deux triangles isocèles. En imaginant un carré sur cette diagonale, il aurait déduit que son aire était égale à la somme des carrés construits sur les deux autres côtés. Un bel exemple de la façon dont une observation banale peut inspirer une idée mathématique majeure.
• Triplets pythagoriciens
  Un triplet pythagoricien est un ensemble de trois entiers positifs (a, b, c) qui satisfont l’équation : $$ a^2 + b^2 = c^2 $$

Et ainsi de suite.