Critères de congruence des triangles
Les trois critères de congruence des triangles permettent de savoir si deux triangles sont congruents à partir d'un nombre limité d'informations géométriques.
En géométrie, deux figures sont dites congruentes lorsqu'elles peuvent être superposées exactement au moyen d'un mouvement rigide, c'est-à-dire une transformation qui conserve les longueurs et les angles.
Cette notion s'applique naturellement aux triangles. Dans sa définition la plus stricte, elle supposerait de connaître tous les éléments de la figure.
Il existe toutefois trois critères fondamentaux de congruence qui permettent d'établir la congruence de deux triangles à partir de seulement trois éléments bien choisis.
Pourquoi utiliser les critères de congruence ? Parce qu'ils reposent sur la comparaison de côtés et d'angles sans qu'il soit nécessaire d'examiner toutes les correspondances point par point. La méthode est ainsi plus simple, plus rapide et parfaitement adaptée à un raisonnement fondé sur des données partielles.
Premier critère de congruence des triangles
Deux triangles sont congruents s'ils possèdent deux côtés congruents et l'angle compris entre ces côtés, disposés dans le même ordre.
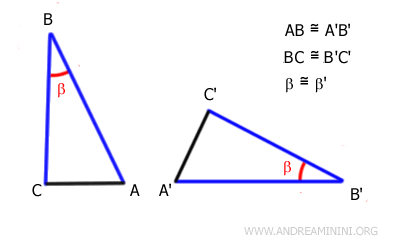
Concrètement, cela signifie que deux triangles ont la même forme et la même taille dès qu'ils partagent deux côtés de même longueur et l'angle formé par ces côtés.
Ce critère est appelé critère Côté-Angle-Côté (CAC), ou encore SAS (Side-Angle-Side) dans la littérature internationale.
Il est important de souligner que l'angle considéré doit impérativement être l'angle compris entre les deux côtés. Dans le cas contraire, la congruence n'est pas assurée.
Considérons par exemple le triangle ABC. On trace un cercle de centre A et de rayon AC. L'arc obtenu coupe le prolongement du segment AC en un point D, ce qui permet de construire un nouveau triangle ACD.
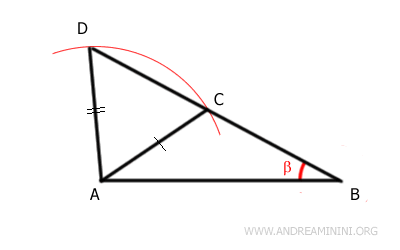
Les triangles ABC et ABD ne sont pas congruents. Bien qu'ils possèdent deux côtés congruents, AB ≅ AB et AC ≅ AD, ainsi qu'un angle congruent β, cet angle n'est pas l'angle compris entre les deux côtés. La connaissance de deux côtés et d'un angle non compris entre eux ne suffit donc pas à garantir la congruence.
Le premier critère de congruence est généralement admis comme un postulat.
Deuxième critère de congruence des triangles
Deux triangles sont congruents s'ils possèdent deux angles congruents et le côté compris entre ces angles, disposés dans le même ordre.
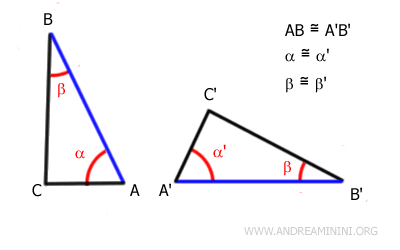
Autrement dit, deux triangles sont congruents lorsqu'ils ont deux angles de même mesure et que le côté situé entre ces deux angles est congruent.
Ce critère est également connu sous le nom de critère Angle-Côté-Angle (ACA) ou ASA (Angle-Side-Angle).
Contrairement au premier, ce critère est un théorème, car il peut être démontré de façon rigoureuse.
Un résultat fondamental de la géométrie euclidienne établit que la somme des angles intérieurs d'un triangle est égale à un angle plat, soit 180°. Ainsi, lorsque deux angles sont connus, le troisième est entièrement déterminé par un simple calcul.
Ce critère admet également une forme plus générale, appelée deuxième critère généralisé ou quatrième critère de congruence des triangles.
Deux triangles sont congruents s'ils possèdent deux angles congruents et un côté congruent, disposés dans le même ordre, même si ce côté n'est pas nécessairement compris entre les deux angles.
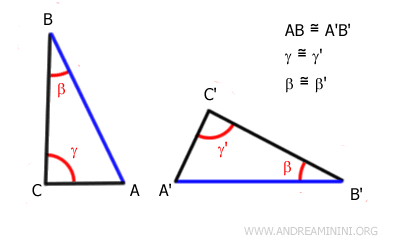
Dans ce cas, le côté congruent peut être n'importe lequel des trois côtés du triangle.
Troisième critère de congruence des triangles
Deux triangles sont congruents s'ils possèdent leurs trois côtés congruents.
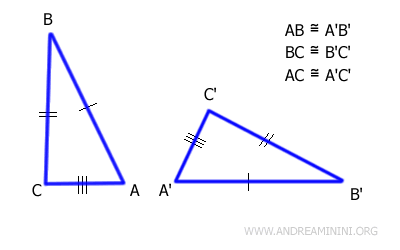
En pratique, deux triangles sont congruents lorsque tous leurs côtés ont la même longueur.
Ce critère est également appelé critère Côté-Côté-Côté (CCC) ou SSS (Side-Side-Side).
Comme le précédent, il s'agit d'un théorème démontrable de manière rigoureuse.
Remarque : La congruence des angles seuls (AAA) est une condition nécessaire mais non suffisante pour la congruence des triangles. Deux triangles peuvent avoir les mêmes angles tout en ayant des côtés de longueurs différentes. Ils ont alors la même forme, mais une échelle différente, et ne sont donc pas congruents. En revanche, deux triangles dont les côtés sont congruents (CCC) possèdent nécessairement des angles congruents. Ainsi, le critère AAA ne constitue pas un critère valide de congruence.
Et ainsi de suite.