Somme des angles intérieurs d’un triangle
Dans tout triangle, la somme des angles intérieurs est toujours égale à un angle plat, c’est-à-dire 180°.
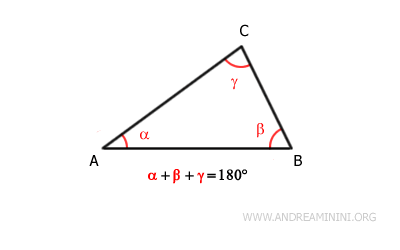
Cette propriété fondamentale de la géométrie plane s’exprime de manière simple par la relation suivante :
$$ \alpha + \beta + \gamma = 180° $$
Démonstration
Considérons un triangle quelconque ABC.
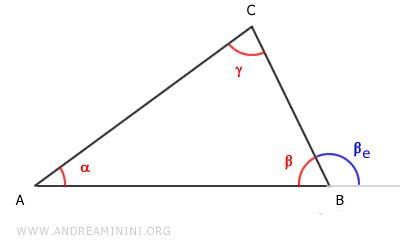
L’angle extérieur $ \beta_e $ est supplémentaire de l’angle intérieur $ \beta $. Autrement dit, la somme de ces deux angles forme un angle plat :
$$ \beta + \beta_e = 180° $$
D’après le théorème de l’angle extérieur, un angle extérieur d’un triangle est égal à la somme des deux angles intérieurs qui ne lui sont pas adjacents :
$$ \beta_e \cong \alpha + \gamma $$
En combinant ces deux résultats, on obtient :
$$ \beta + (\alpha + \gamma) = 180° $$
Ce qui conduit directement à la relation recherchée :
$$ \alpha + \beta + \gamma = 180° $$
La démonstration montre ainsi que, quel que soit le triangle considéré, la somme de ses angles intérieurs vaut toujours 180°.
Démonstration alternative
Reprenons le même triangle ABC et adoptons une approche géométrique différente.
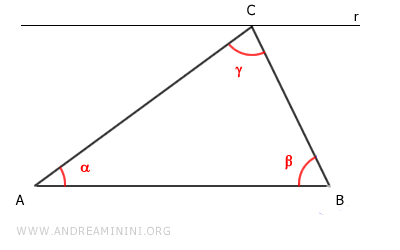
Par le sommet C, on trace une droite parallèle au côté AB du triangle.
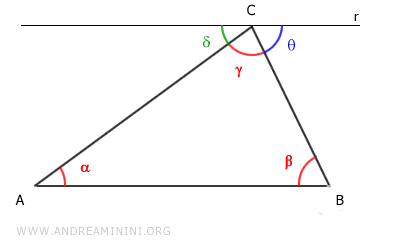
Les angles $ \delta $, $ \gamma $ et $ \theta $, alignés sur cette droite, constituent ensemble un angle plat :
$$ \delta + \gamma + \theta = 180° $$
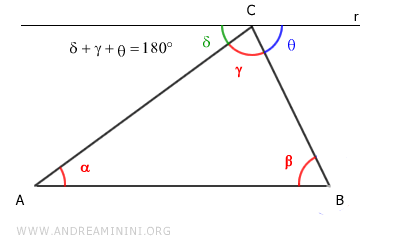
Selon le théorème des droites parallèles, les angles alternes-internes déterminés par une transversale et deux droites parallèles sont égaux :
- $ \alpha \cong \delta $, par rapport à la transversale AC.
- $ \beta \cong \theta $, par rapport à la transversale BC.
On peut alors écrire :
$$ \alpha + \beta + \gamma = \delta + \theta + \gamma = 180° $$
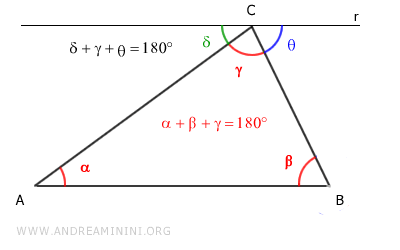
Cette seconde démonstration confirme, d’un point de vue géométrique, que la somme des angles intérieurs d’un triangle est toujours égale à 180°.
Et ainsi de suite.