Triangle isocèle

Un triangle isocèle est une figure géométrique plane à trois côtés dont deux ont la même longueur. Ces deux côtés sont appelés côtés égaux ou côtés isocèles.

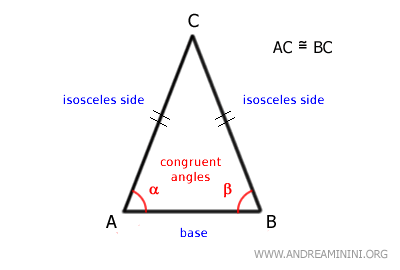
Le troisième côté est appelé la base du triangle.

Les deux côtés égaux déterminent deux angles à la base, qui ont la même mesure.

L'angle opposé à la base est appelé angle au sommet.

Origine du terme isocèle. Le mot « isocèle » vient du grec ancien. « Isos » signifie « égal » et « skelos » désigne la « jambe » ou le « côté ». Le terme signifie donc littéralement « à côtés égaux », ce qui décrit avec précision ce type de triangle.

Un exemple concret

Considérons le triangle ABC.

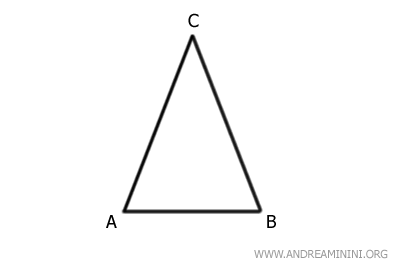
Les côtés AC et BC sont congruents, c'est-à-dire qu'ils ont la même longueur.

Ils constituent les côtés égaux, aussi appelés côtés isocèles, du triangle.

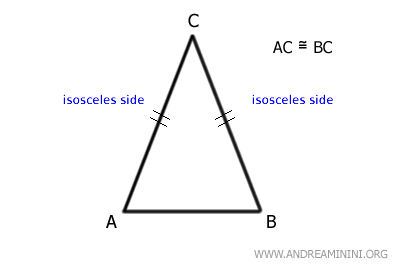
Le côté restant, AB, qui n'est pas congruent aux deux autres, est la base du triangle.

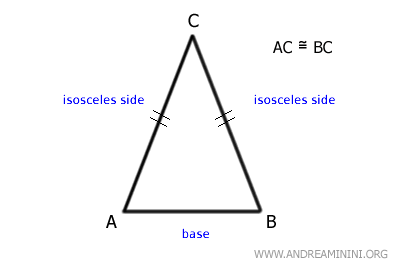
Les côtés isocèles forment deux angles égaux, situés de part et d'autre de la base.

Ces angles sont appelés angles à la base.

On peut aussi décrire ABC comme un « triangle isocèle de sommet C ».

Remarques et propriétés

Les triangles isocèles présentent plusieurs propriétés importantes, utiles aussi bien en géométrie élémentaire qu'en résolution de problèmes :

• Un triangle isocèle possède deux côtés congruents (AC≅BC)
  

  

• Théorème du triangle isocèle

  Un triangle est isocèle si, et seulement si, il possède deux angles égaux (α≅β).

  Cette propriété repose sur un principe fondamental de la géométrie plane : dans tout triangle, les côtés opposés à des angles de même mesure sont eux-mêmes de même longueur.
  

  Remarque. Autrement dit, un triangle ayant deux angles égaux est isocèle, et tout triangle isocèle possède nécessairement deux angles égaux.

• Les angles à la base d'un triangle isocèle sont toujours aigus
  
  Puisqu'ils sont égaux, ces angles ne peuvent être ni droits ni obtus. Dans un triangle, il est impossible d'avoir deux angles droits ou deux angles obtus simultanément.
  

  Justification. Si les deux angles à la base étaient droits ou obtus, on contredirait le théorème sur la somme des angles intérieurs, selon lequel tout triangle possède au moins deux angles aigus. Un triangle ne peut donc comporter qu'un seul angle non aigu.

• La bissectrice dans un triangle isocèle

  Dans un triangle isocèle, la bissectrice de l'angle au sommet coïncide avec la médiane, la hauteur et la médiatrice de la base.

  
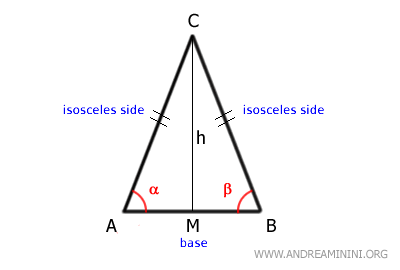
  Cette hauteur (h), tracée du sommet vers la base, partage le triangle en deux triangles rectangles congruents (AMC≅BCM) et coupe la base en deux segments de même longueur (AM≅BM).
• Le triangle équilatéral est un cas particulier de triangle isocèle dans lequel les trois côtés ont la même longueur. Ainsi, tout triangle équilatéral est isocèle, mais l'inverse n'est pas vrai. Dans un triangle équilatéral, n'importe quel côté peut servir de base, et chacun des trois angles mesure 60°.
  
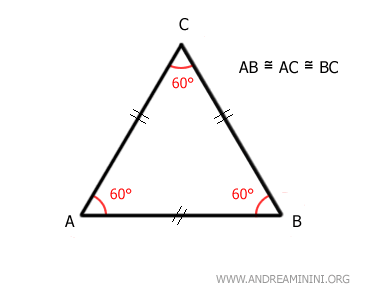
• La somme des angles intérieurs de tout triangle, y compris du triangle isocèle, est toujours égale à 180 degrés.
• Un triangle isocèle peut être aigu, rectangle ou obtus, selon la mesure de son angle au sommet.
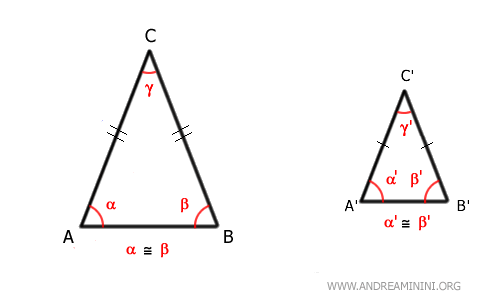
• Deux triangles isocèles sont semblables s'ils ont le même angle au sommet
  Deux triangles isocèles sont semblables lorsqu'ils partagent le même angle au sommet, c'est-à-dire l'angle compris entre les deux côtés égaux. Comme la somme des angles intérieurs d'un triangle vaut 180 degrés, si les angles au sommet γ≅γ' sont égaux, alors les angles à la base de chaque triangle sont égaux à (180° - γ) ÷ 2. Les trois angles correspondants sont donc congruents et, d'après le premier critère de similitude des triangles, les deux triangles sont semblables. Ils ont la même forme, sans nécessairement avoir la même taille.
  

Et ainsi de suite.