Théorème de l’angle extérieur d’un triangle

Dans tout triangle, un angle extérieur ($ \beta_e $) est strictement plus grand que chacun des angles intérieurs non adjacents ($ \alpha $ et $ \gamma $).

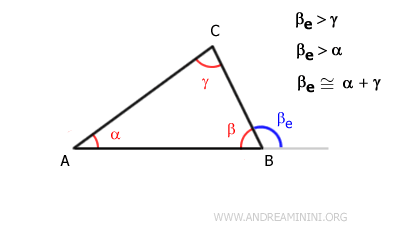
Cette propriété repose sur un résultat fondamental: tout angle extérieur d’un triangle est égal à la somme des deux angles intérieurs non adjacents:
$$ \beta_e = \alpha + \gamma $$

Ce théorème appartient aux bases de la géométrie euclidienne et s’applique à tous les triangles, quelle que soit leur forme.

Dans le triangle ABC, par exemple, l’angle extérieur situé au sommet B, noté $ \beta_e $, est strictement plus grand que chacun des angles intérieurs $ \alpha $ et $ \gamma $.

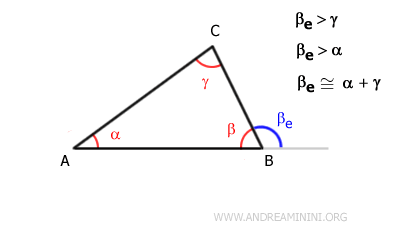
Autrement dit, dans un triangle, l’angle extérieur est toujours plus grand que tout angle intérieur qui ne lui est pas adjacent.

Démonstration

Considérons un triangle ABC.

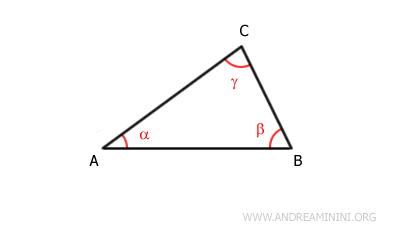
Prolongeons le côté $ AB $ au-delà du sommet $ B $. On obtient ainsi l’angle extérieur $ \beta_e $, qui est supplémentaire de l’angle intérieur $ \beta $.

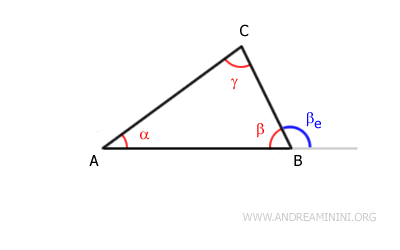
Traçons ensuite, par le sommet $ B $, la droite $ BE $ parallèle au côté $ AC $.

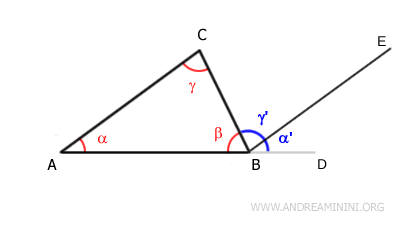
Par construction, l’angle extérieur $ \beta_e $ est formé par la somme des angles $ \alpha' $ et $ \gamma' $:

$$ \beta_e = \alpha' + \gamma' $$

D’après le théorème des droites parallèles, les droites $ BE $ et $ AC $ étant parallèles et coupées par la transversale $ CB $, les angles alternes-internes sont égaux:

$$ \gamma = \gamma' $$

De la même manière, ces droites parallèles, coupées cette fois par la transversale $ AB $, déterminent des angles correspondants égaux:

$$ \alpha = \alpha' $$

Remarque: Le théorème des droites parallèles est utilisé deux fois sur les mêmes droites $ BE $ et $ AC $, en considérant deux transversales différentes.

On obtient ainsi la relation fondamentale:

$$ \beta_e = \alpha + \gamma $$

Comme cette somme est nécessairement supérieure à chacun de ses termes, on en déduit immédiatement que:

$$ \beta_e > \alpha $$

$$ \beta_e > \gamma $$

La démonstration montre donc à la fois que l’angle extérieur est plus grand que chacun des angles intérieurs non adjacents, et que sa mesure est exactement égale à leur somme.

Démonstration alternative

A] L’angle extérieur est plus grand que les angles intérieurs non adjacents

Considérons un triangle quelconque ABC.

Intéressons-nous à l’angle extérieur au sommet B, noté $ \beta_e $.

Nous allons montrer, par une construction géométrique, que cet angle est plus grand que chacun des angles intérieurs non adjacents $ \alpha $ et $ \gamma $.

Première partie

Soit M le milieu du côté $ BC $, adjacent à l’angle $ \beta $. Traçons la médiane $ AM $.

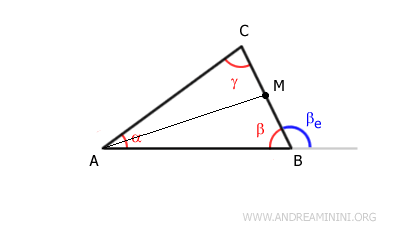
Par définition du milieu, on a:

$$ BM \cong CM $$

Prolongeons ensuite le segment $ AM $ en ajoutant un segment $ ME $ de même longueur.

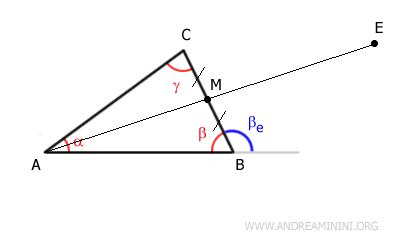
On obtient alors:

$$ BM \cong CM $$

$$ AM \cong ME $$

Relions les points $ B $ et $ E $ par le segment $ BE $.

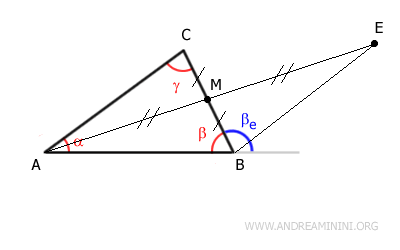
Au point M, les segments se coupent et forment deux angles opposés par le sommet, donc égaux:

$$ \theta_1 \cong \theta_2 $$

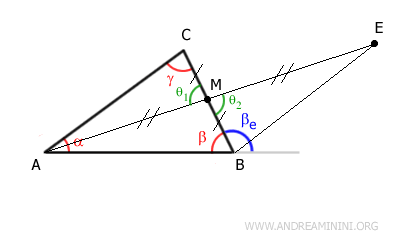
D’après le critère de congruence côté-angle-côté, les triangles $ AMC $ et $ BME $ sont congruents.

$$ AMC \cong BME $$

Il en résulte que les angles correspondants sont égaux, en particulier:

$$ \gamma \cong \delta $$

Or l’angle $ \delta $ est strictement inférieur à l’angle extérieur $ \beta_e $, puisque le segment $ BE $ partage ce dernier en deux parties:

$$ \delta < \beta_e $$

On en déduit immédiatement que:

$$ \gamma < \beta_e $$

L’angle extérieur $ \beta_e $ est donc plus grand que l’angle intérieur $ \gamma $.

Deuxième partie

Un raisonnement entièrement analogue permet de montrer que l’angle extérieur est également plus grand que l’angle $ \alpha $.

Soit M le milieu du côté $ AB $, adjacent à $ \beta $. Traçons la médiane $ CM $.

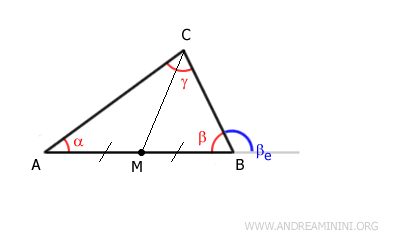
On a alors:

$$ \overline{AM} \cong \overline{BM} $$

Prolongeons le segment $ CM $ en ajoutant un segment $ MF $ de même longueur.

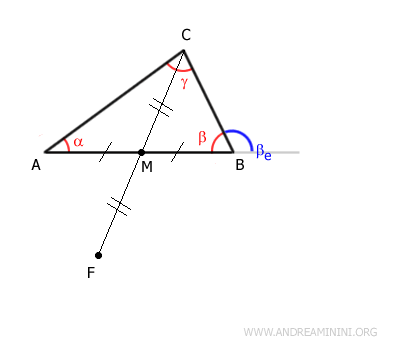
Il en résulte:

$$ \overline{CM} \cong \overline{MF} $$

Relions les points $ B $ et $ F $ par le segment $ BF $.

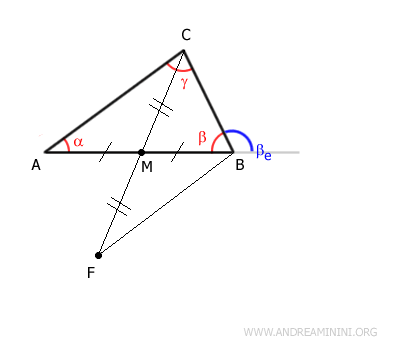
Les angles opposés par le sommet formés au point M sont égaux:

$$ \theta_1 \cong \theta_2 $$

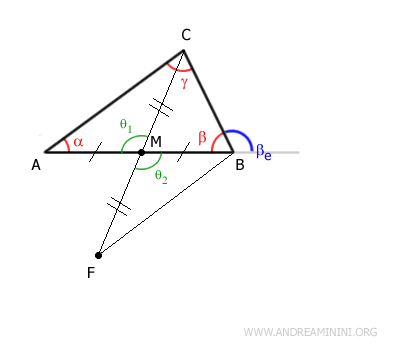
Les triangles $ AMC $ et $ BMF $ sont donc congruents ( critère de congruence côté-angle-côté ), ce qui implique:

$$ \alpha \cong \delta $$

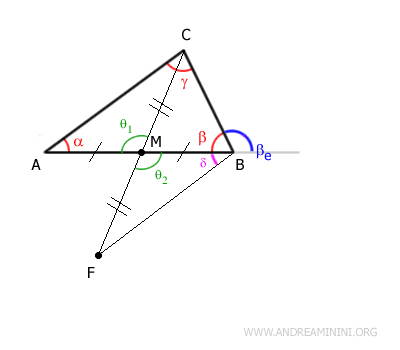
En comparant cet angle $ \delta $ avec l’angle extérieur $ \beta_e $, on observe que:

$$ \delta < \beta_e $$

Comme $ \delta \cong \alpha $, on conclut que:

L’angle extérieur $ \beta_e $ est plus grand que l’angle intérieur $ \alpha $.

Conclusion

Dans tout triangle, l’angle extérieur $ \beta_e $ est strictement plus grand que les angles intérieurs non adjacents $ \alpha $ et $ \gamma $.

Le théorème de l’angle extérieur d’un triangle est ainsi établi de manière claire et rigoureuse.

B] L'angle extérieur est égal à la somme des angles intérieurs non adjacents

Montrons à présent que l'angle extérieur d'un triangle est exactement égal à la somme des deux angles intérieurs non adjacents.

Considérons le triangle ABC et l'angle extérieur $ \beta_e $ associé au sommet B.

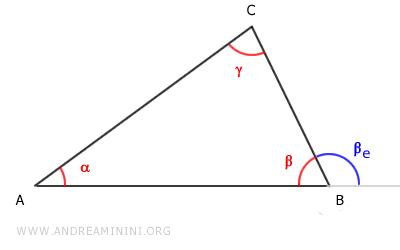
Traçons les droites supports des côtés du triangle, que nous notons a, b et c.

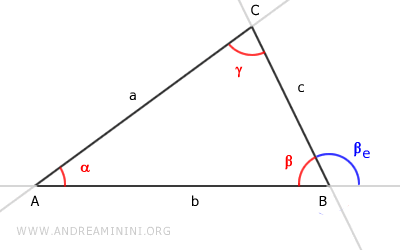
Traçons ensuite une droite d, parallèle au côté $ AC $, passant par le sommet $ B $.

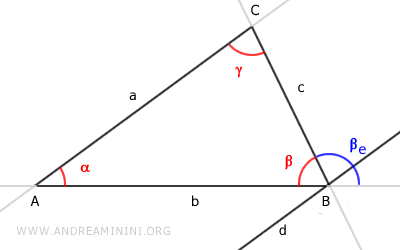
Cette construction permet de décomposer l'angle extérieur en deux angles adjacents:
$ \beta_e = \beta'_e + \beta''_e $

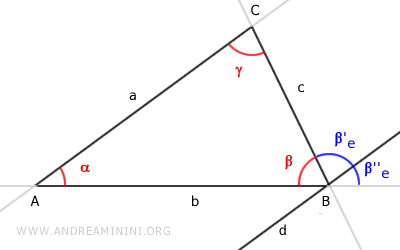
L'angle $ \beta'_e $ est un angle alternes-internes formé par les droites parallèles a et d, coupées par la transversale c.

D'après le théorème des droites parallèles, les angles alternes-internes $ \gamma $ et $ \beta'_e $ sont égaux:
$ \gamma \cong \beta'_e $.

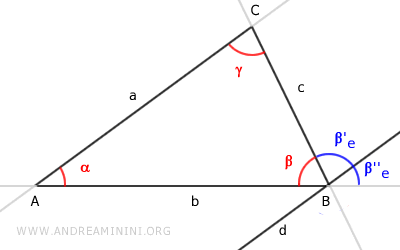
L'angle $ \beta''_e $ est un angle correspondant formé par les droites parallèles a et d, coupées par la transversale b.

Par le même théorème, les angles correspondants $ \alpha $ et $ \beta''_e $ sont égaux:
$ \alpha \cong \beta''_e $.

Or, puisque l'angle extérieur est la somme:
$ \beta_e = \beta'_e + \beta''_e $, et que:
$ \gamma \cong \beta'_e $ et $ \alpha \cong \beta''_e $, on en déduit immédiatement:

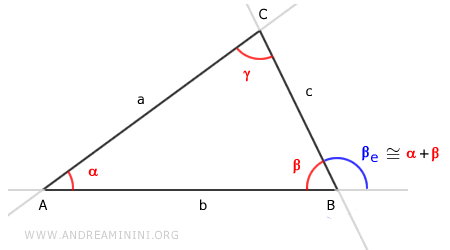
$$ \beta_e \cong \gamma + \alpha $$

L'angle extérieur $ \beta_e $ est donc égal à la somme des angles intérieurs non adjacents du triangle.

Observations

Ce résultat fondamental entraîne plusieurs conséquences importantes en géométrie.

• La somme des angles intérieurs d'un triangle est égale à 180°
  Dans tout triangle, la somme des trois angles intérieurs est toujours égale à 180°, c'est-à-dire à un angle plat. Cette propriété constitue un invariant géométrique, indépendant de la forme du triangle.
  

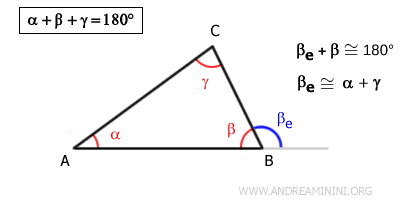
  Démonstration. Un angle intérieur et son angle extérieur adjacent sont supplémentaires. Par exemple:
  $$ \beta + \beta' = 180° $$
  Or:
  $$ \beta' = \alpha + \gamma $$
  D'où:
  $$ \alpha + \beta + \gamma = 180° $$

• La somme de deux angles intérieurs est toujours strictement inférieure à 180°
  C'est un corollaire direct du théorème de l'angle extérieur. Puisque l'angle extérieur est strictement supérieur à chacun des angles intérieurs non adjacents, on obtient:
  $$ \alpha + \gamma < 180° $$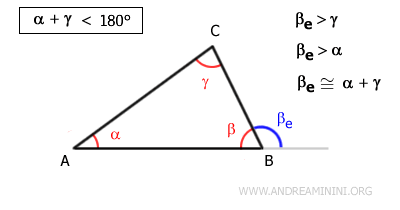

  

• Un triangle ne peut avoir qu'un seul angle droit ou qu'un seul angle obtus
  Cette propriété découle directement de la somme des angles égale à 180°.

  Remarque. Deux angles droits ou deux angles obtus dans un même triangle rendraient impossible la somme totale de 180°.

• Autres conséquences utiles
  
  • Dans un triangle rectangle, les deux angles aigus sont complémentaires
    Leur somme est égale à 90°.
  • Dans un triangle équilatéral, chaque angle intérieur mesure 60°
    Les trois angles étant égaux et leur somme valant 180°.
  • Si deux triangles ont deux angles respectivement égaux, alors le troisième angle est également égal
    Ce principe repose directement sur la constance de la somme des angles.

    Remarque. Ce résultat est à la base du critère généralisé ASA de congruence des triangles.

Ces propriétés montrent le rôle central du théorème de l'angle extérieur dans l'étude des triangles.