Deuxième critère de congruence des triangles
Deux triangles sont dits congruents lorsqu’ils possèdent deux angles correspondants de même mesure et que le côté compris entre ces deux angles a la même longueur dans les deux triangles.
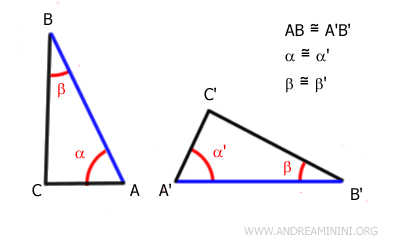
En pratique, cela signifie que pour reconnaître deux triangles congruents, il suffit de vérifier l’égalité de deux angles et du côté situé entre eux.
Ce résultat est connu sous le nom de critère Angle-Côté-Angle (ACA), ou ASA (Angle-Side-Angle) dans la terminologie internationale.
Illustrons ce critère à l’aide des triangles ABC et A'B'C'.
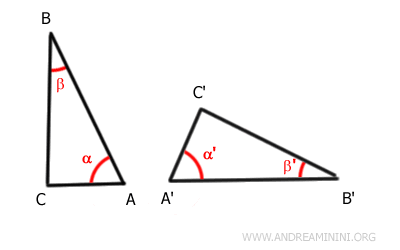
Les angles α≅α' et β≅β' ont la même mesure.
Le côté compris entre ces deux angles est également de même longueur dans les deux triangles, puisque AB ≅ A'B'.
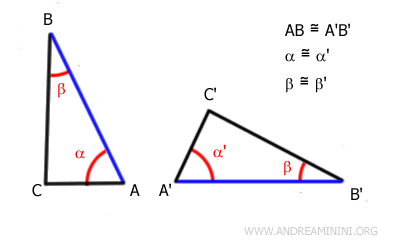
Ces informations suffisent pour conclure que tous les autres côtés et angles correspondants sont eux aussi égaux.
On peut donc affirmer que les deux triangles sont congruents. Autrement dit, il est possible de superposer l’un à l’autre par un simple mouvement rigide.
Démonstration
Le deuxième critère de congruence n’est pas une simple règle pratique, mais un véritable théorème qui peut être démontré rigoureusement.
Considérons de nouveau les triangles ABC et A'B'C'.
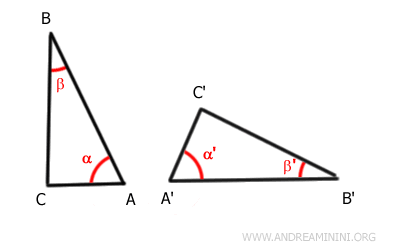
Par hypothèse, les angles α≅α' et β≅β' sont congruents, tout comme le côté AB ≅ A'B' compris entre eux.
Comme les côtés AB et A'B' ont la même longueur, on peut les faire coïncider par un mouvement rigide.
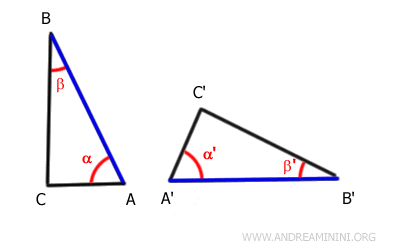
Les extrémités de ces côtés se superposent alors naturellement, le point A avec A' et le point B avec B'.
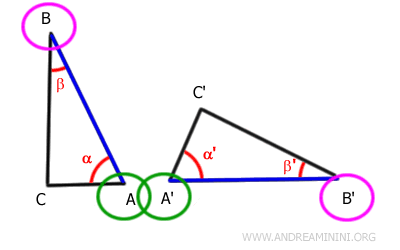
Les angles α et α' étant égaux, les demi-droites supportant les côtés AC et A'C' coïncident.
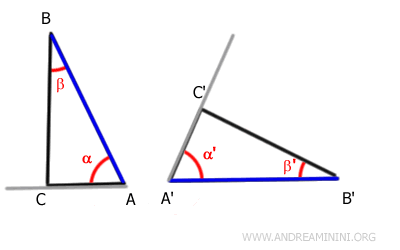
De la même façon, l’égalité des angles β et β' entraîne la coïncidence des demi-droites supportant les côtés BC et B'C'.
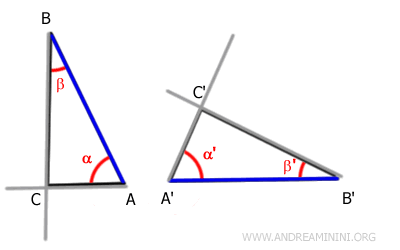
Ces demi-droites se coupent en un unique point.
On en déduit que les points C et C' coïncident.
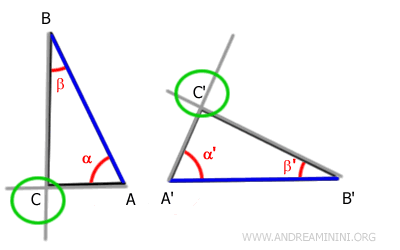
Ainsi, les trois sommets des deux triangles coïncident dans le même ordre.
Il en résulte que tous les côtés correspondants sont égaux, AB ≅ A'B', BC ≅ B'C', AC ≅ A'C'.
Par conséquent, tous les angles correspondants sont également congruents.
Les deux triangles sont donc congruents.
Démonstration alternative
On peut également établir ce résultat par une démonstration par l’absurde.
Supposons que deux triangles ABC et A'B'C' vérifient les conditions suivantes : deux angles congruents, \( \alpha \cong \alpha' \) et \( \beta \cong \beta' \), ainsi qu’un côté congruent, \( AB \cong A'B' \).
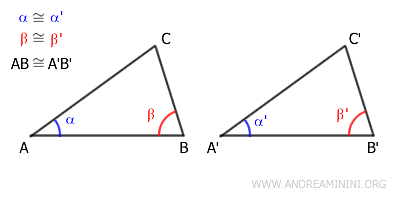
Supposons néanmoins que ces deux triangles ne soient pas congruents.
$$ ABC \not \cong A'B'C' $$
Dans ce cas, le côté AC devrait être soit plus long, soit plus court que A'C'.
Supposons que AC soit plus long, c’est-à-dire $ AC > A'C' $. On peut alors choisir un point P sur le segment AC tel que $ AP \cong A'C' $.
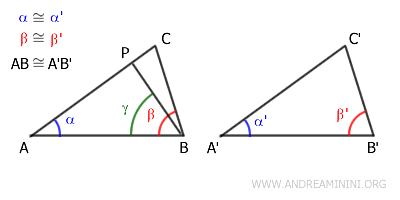
Examinons les triangles ABP et A'B'C'. Ils possèdent :
- un angle congruent par hypothèse, \( \alpha \cong \alpha' \) ;
- un côté congruent par hypothèse, \( AB \cong A'B' \) ;
- un second côté congruent par construction, \( AP \cong A'C' \).
D’après le premier théorème de congruence, ces deux triangles doivent alors être congruents.
$$ ABP \cong A'B'C' $$
Il s’ensuit que les angles correspondants \( \gamma \) et \( \beta' \) sont égaux.

Or, comme \( \beta \cong \beta' \), on obtient par transitivité \( \gamma \cong \beta \).
$$ \gamma \cong \beta' \cong \beta $$
Cette conclusion est impossible, car le point \( P \) étant situé à l’intérieur du segment \( AC \), l’angle \( \gamma \) est nécessairement plus petit que l’angle \( \beta \).
La supposition initiale est donc fausse.
On conclut ainsi que les deux triangles sont nécessairement congruents.
Remarque : Un raisonnement identique s’applique si l’on suppose que \( AC < A'C' \). Dans tous les cas, on obtient nécessairement \( AC \cong A'C' \).
Critère généralisé de congruence ACA des triangles
Le deuxième critère de congruence des triangles peut être étendu sous une forme plus générale, couramment appelée critère généralisé de congruence, et parfois présentée comme le quatrième critère de congruence dans les manuels de géométrie.
Deux triangles sont congruents s'ils possèdent deux angles congruents et un côté congruent disposés dans le même ordre relatif, même si ce côté n'est pas nécessairement compris entre les deux angles.
Dans cette configuration, le côté congruent peut être n'importe lequel des trois côtés du triangle. Il n'est donc pas indispensable qu'il s'agisse du côté situé entre les deux angles congruents.
Autrement dit, les deux angles égaux ne sont pas nécessairement adjacents au côté égal.
En revanche, une condition essentielle doit être respectée : les angles et le côté doivent apparaître dans le même ordre relatif dans les deux triangles.
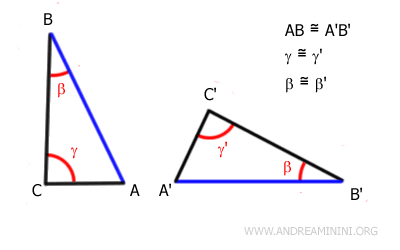
Exemple. Les deux triangles représentés ci-dessous possèdent des angles correspondants $ \alpha \cong \alpha' $ et $ \beta \cong \beta' $, ainsi qu'un côté congruent $ BC \cong B'C' $. Comme ces éléments apparaissent dans le même ordre relatif, on peut appliquer le critère généralisé ACA et conclure que $ ABC \cong A'B'C' $.

Jusqu'ici, tout est cohérent. Considérons maintenant le triangle ABC et, de centre A, traçons un arc de cercle de rayon AB qui coupe le segment AC en un point C'. Traçons ensuite le segment B'C' parallèle à BC. On obtient ainsi un nouveau triangle AB'C'. Par construction, ces triangles présentent également deux angles égaux $ \alpha $ et $ \beta \cong \beta' $, ainsi qu'un côté congruent $ AB \cong A'B' $. Toutefois, les triangles ne sont pas congruents, $ ABC \not \cong AB'C' $, car les angles et le côté ne sont pas disposés dans le même ordre relatif.
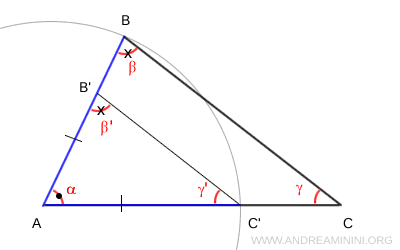
Cet exemple montre clairement que l'ordre relatif des éléments est déterminant pour l'application du critère généralisé ACA.
Démonstration
D'après le théorème de la somme des angles intérieurs d'un triangle, la somme des trois angles intérieurs d'un triangle est toujours égale à 180°.
$$ \alpha + \beta + \gamma = 180° $$
Il en résulte que, si deux angles des triangles ABC et A'B'C' sont congruents, $ \alpha \cong \alpha' $ et $ \beta \cong \beta' $, le troisième angle est nécessairement congruent par différence, c'est-à-dire $ \gamma \cong \gamma' $.
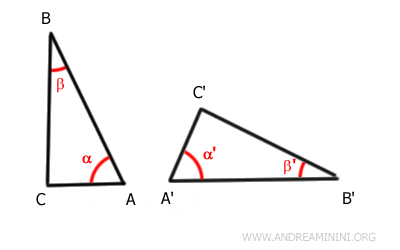
L'angle restant $\gamma$ dans chacun des deux triangles se calcule donc de la façon suivante :
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma' = 180° - \alpha' - \beta' $$
Comme $ \alpha \cong \alpha' $ et $ \beta \cong \beta' $, on obtient immédiatement $ \gamma \cong \gamma' $.
Supposons maintenant que les triangles ABC et A'B'C' possèdent également un côté congruent, par exemple $ BC \cong B'C' $, et que ce côté occupe la même position relative dans les deux triangles.
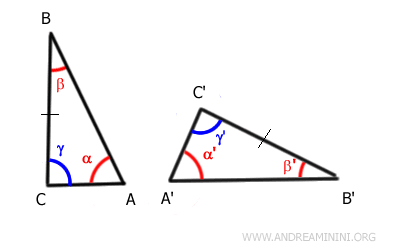
Dans ces conditions, puisque $ \gamma \cong \gamma' $ et $ \beta \cong \beta' $, on peut conclure que les triangles $ ABC \cong A'B'C' $ sont congruents par application du critère ACA, puisqu'ils présentent deux angles adjacents à un côté congruent, disposés dans le même ordre.
On en déduit que deux triangles sont congruents dès lors qu'ils possèdent deux angles et un côté congruents, même si ce côté n'est pas le côté compris entre les deux angles.
Démonstration alternative
Le critère généralisé de congruence peut également être établi à l'aide d'un raisonnement par l'absurde.
Considérons deux triangles ABC et A'B'C'.

Par hypothèse, les angles $ \alpha \cong \alpha' $ et $ \beta \cong \beta' $ sont congruents, et le côté compris entre eux, AB ≅ A'B', est également congruent.
D'après le deuxième critère de congruence, les deux triangles devraient donc être congruents.
Pour obtenir une contradiction, supposons que les côtés AC et A'C' ne soient pas congruents, c'est-à-dire que $ AC \ne A'C' $.
D'après le postulat du report des segments, on peut placer un point D sur le segment AC tel que $ AD = A'C' $.
On trace alors le segment BD et l'on considère le triangle ABD.
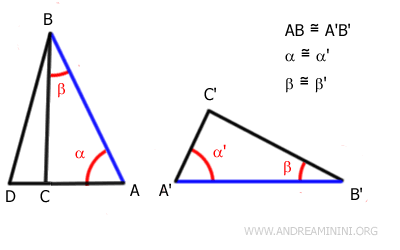
D'après le premier critère de congruence, les triangles ABD et A'B'C' sont congruents.
Pourquoi ? Par construction, $ AD \cong A'C' $. Par hypothèse, $ AB \cong A'B' $, et l'angle compris $ \alpha \cong \alpha' $. Les conditions du premier critère (Côté-Angle-Côté) sont donc réunies, ce qui implique $ ABD \cong A'B'C' $.
Il en résulte que les angles aux sommets D et C' sont congruents.
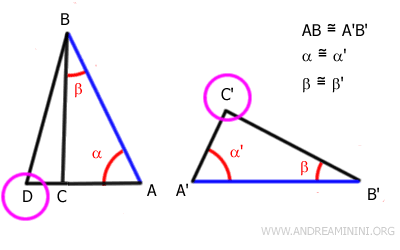
Or, par hypothèse initiale, les angles aux sommets C et C' étaient déjà congruents, puisque $ \gamma \cong \gamma' $.
D'après le théorème de la somme des angles intérieurs : $$ \alpha + \beta + \gamma = 180° $$ Si deux angles sont congruents, le troisième l'est également : $$ \gamma = 180° - \alpha - \beta $$ $$ \gamma' = 180° - \alpha' - \beta' $$ $$ \gamma \cong \gamma' $$
Par transitivité, l'angle au sommet D est donc congruent à l'angle au sommet C.
Il s'ensuit que $ AD \cong AC $.
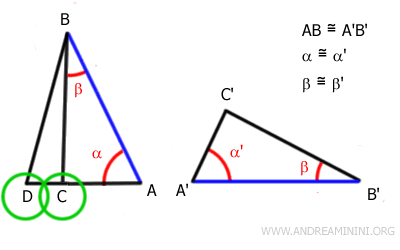
Or, puisque l'on avait déjà $ AD \cong A'C' $, on obtient nécessairement $ AC \cong A'C' $.
$$ \overline{AC} \cong \overline{AD} \cong \overline{A'C'} $$
Cette conclusion contredit l'hypothèse initiale selon laquelle $ AC \ne A'C' $.
L'hypothèse est donc fausse, et l'on doit nécessairement avoir $ AC \cong A'C' $.
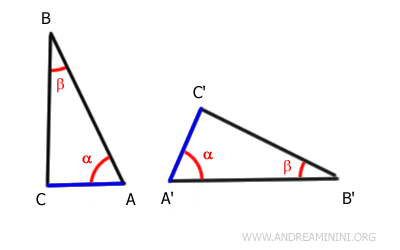
En conclusion, pour établir la congruence de deux triangles, il suffit qu'ils possèdent deux angles et un côté congruents, même si ce côté n'est pas le côté compris entre les deux angles.
Et ainsi de suite.