Premier critère de congruence des triangles
Le premier critère de congruence des triangles indique que deux triangles sont congruents lorsqu'ils possèdent deux côtés de même longueur et l'angle compris entre ces côtés, également de même mesure, disposés dans le même ordre.
En pratique, cela signifie que si deux triangles partagent deux côtés égaux et l'angle formé par ces côtés, alors ils ont exactement la même forme et la même taille.
Ce critère est connu sous le nom de critère Côté-Angle-Côté (CAC). Dans la littérature internationale, on le rencontre aussi sous l'acronyme SAS (Side-Angle-Side).
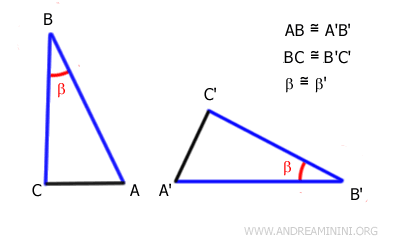
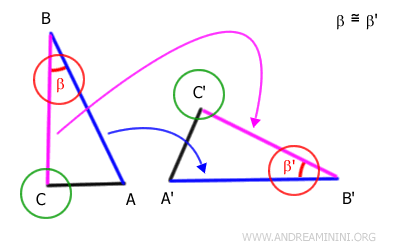
Observons par exemple les deux triangles ABC et A'B'C'.
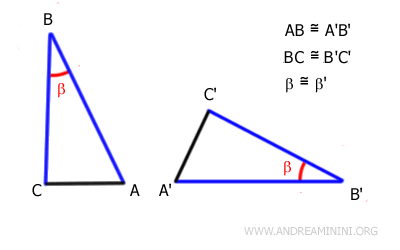
Les côtés AB et BC du triangle ABC sont respectivement congruents aux côtés A'B' et B'C' du triangle A'B'C'. Autrement dit, ils ont la même longueur, même si leur position dans le plan est différente.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Les angles β et β', formés par ces paires de côtés, sont eux aussi congruents, c'est-à-dire de même mesure :
$$ \beta \cong \beta' $$
D'après le premier critère de congruence, ces conditions suffisent pour conclure que les deux triangles sont congruents.
Attention toutefois. Si l'angle congruent n'est pas l'angle compris entre les deux côtés, la congruence n'est plus garantie. Considérons le triangle ABC. On trace un cercle de centre A et de rayon AC. L'arc coupe le prolongement de AC en un point D, ce qui permet de construire le triangle ACD.
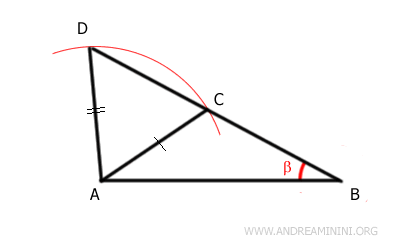
Il est alors clair que les triangles ABC et ABD ne sont pas congruents, car ils ne peuvent pas être superposés. Le triangle ABD est plus grand que le triangle ABC. Pourtant, les deux triangles possèdent deux côtés congruents (AB ≅ AB et AC ≅ AD) ainsi qu'un angle congruent β. Cependant, cet angle n'est pas compris entre les deux côtés congruents. La présence de deux côtés et d'un angle non compris entre eux ne suffit donc pas à assurer la congruence.
Illustration du postulat
Le premier critère de congruence des triangles est formulé comme un postulat, car il repose directement sur les axiomes fondamentaux de la géométrie euclidienne.
La description qui suit ne constitue pas une démonstration formelle au sens strict. Elle s'appuie sur l'idée intuitive des mouvements rigides, c'est-à-dire des transformations qui conservent les longueurs et les angles.
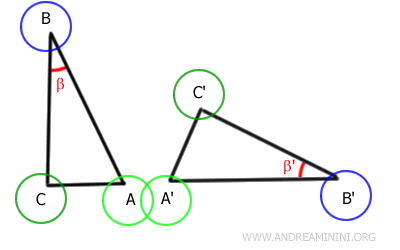
Considérons deux triangles ABC et A'B'C'.
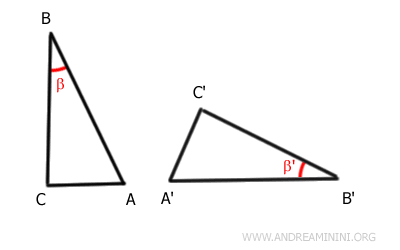
Par hypothèse, les segments AB et A'B', ainsi que BC et B'C', ont la même longueur, et les angles compris β et β' sont congruents.
Appliquons un mouvement rigide, combinaison d'une rotation et d'une translation, qui fait coïncider le côté AB avec le côté A'B'. L'angle β s'aligne alors exactement sur l'angle β'.
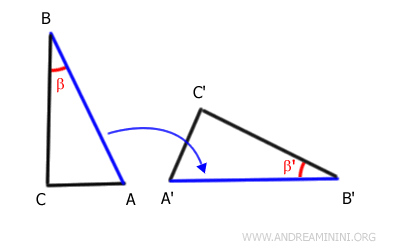
Comme le segment AB se superpose parfaitement au segment A'B', leurs extrémités coïncident.
On en déduit que le point A coïncide avec le point A' et le point B avec le point B'.
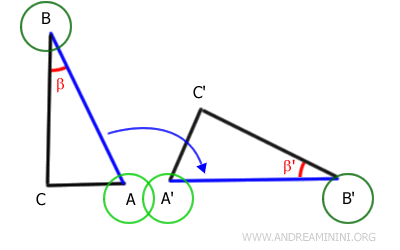
Les angles β et β', adjacents aux côtés désormais superposés, se superposent eux aussi exactement. Cela confirme qu'ils ont la même mesure.
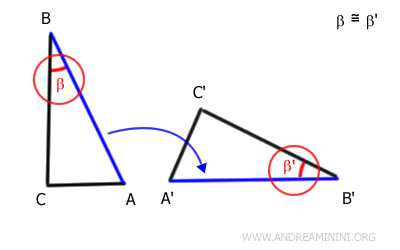
Puisque l'angle compris est congruent et que les côtés adjacents sont égaux, le segment BC se superpose à son tour exactement au segment B'C'.
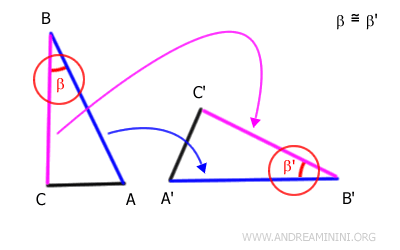
Les extrémités de ces segments correspondent donc également.
Nous avions déjà établi que le point B coïncide avec le point B'. Nous constatons maintenant que le point C coïncide avec le point C'.
Il s'ensuit que le segment AC se superpose lui aussi au segment A'C', puisque leurs extrémités coïncident entièrement.
En conclusion, tous les sommets correspondants des deux triangles coïncident après l'application du mouvement rigide. Il en résulte que tous leurs côtés et tous leurs angles sont congruents, dans le même ordre.
On peut donc conclure que les deux triangles sont congruents.
Et ainsi de suite.