Critère de parallélisme entre deux droites

Il suffit donc de vérifier une seule de ces propriétés pour conclure que deux droites sont parallèles. Dès qu'une condition est satisfaite, les autres en découlent automatiquement.

Ce résultat fondamental est appelé critère de parallélisme.

Remarque : Le théorème réciproque est également vrai. Si deux droites sont parallèles, toute transversale qui les coupe engendre nécessairement des angles alternes congruents, des angles correspondants congruents et des angles conjugués supplémentaires. Ces propriétés caractérisent donc complètement le parallélisme entre deux droites.

Démonstration

Considérons deux droites $ r $ et $ s $ coupées par une transversale. Nous cherchons à montrer qu'elles sont parallèles.

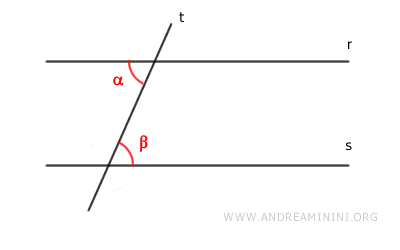
On suppose que deux angles alternes internes sont congruents :

$$ \alpha \cong \beta $$

Raisonnons par l'absurde et supposons que les deux droites se coupent en un point $ C $.

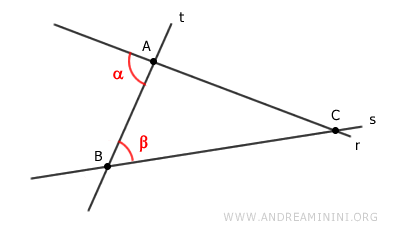
Les deux droites et la transversale formeraient alors le triangle $ ABC $.

D'après le théorème de l'angle extérieur, l'angle extérieur $ \alpha $ est strictement supérieur à l'angle intérieur non adjacent $ \beta $ :

$$ \alpha > \beta $$

Cette inégalité contredit l'hypothèse $ \alpha \cong \beta $.

Il est donc impossible que deux droites coupées par une transversale, présentant des angles alternes internes congruents, se coupent en un point $ C $.

Ne se coupant pas, ces droites sont parallèles. On obtient ainsi le résultat suivant :
deux droites $ r $ et $ s $ qui déterminent des angles alternes internes congruents ($ \alpha \cong \beta $) sont parallèles.

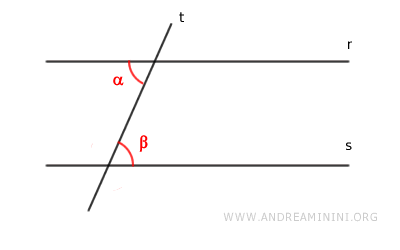
Le critère de parallélisme est donc établi dans le cas des angles alternes internes congruents.

Les autres situations se ramènent à ce cas fondamental :

• Angles alternes externes congruents
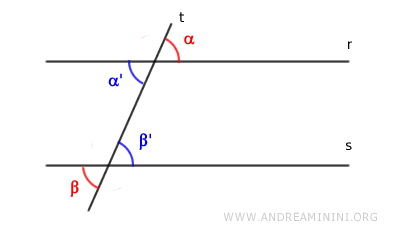
  Si les angles alternes externes sont congruents ($ \alpha \cong \beta $) et qu'ils sont opposés par le sommet aux angles alternes internes ($ \alpha' \cong \alpha $, $ \beta' \cong \beta $), on obtient :
  $$ \alpha' \cong \beta' $$
  
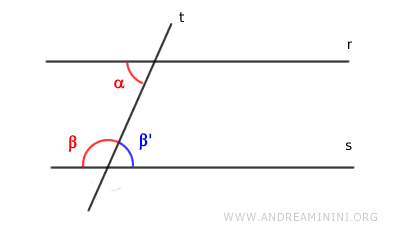
• Angles correspondants congruents
  Si les angles correspondants sont congruents ($ \alpha \cong \beta $) et que chacun est opposé par le sommet à un angle alterne interne, alors :
  $$ \alpha \cong \beta' $$
  
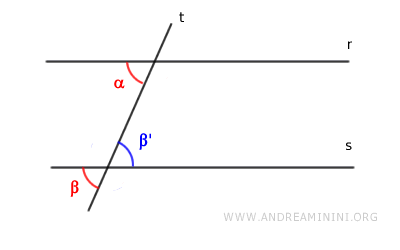
• Angles conjugués supplémentaires
  Si $ \alpha + \beta = 180° $ et que les angles adjacents portés par $ r $ et $ s $ sont également supplémentaires, on en déduit que les angles alternes internes sont congruents :
  $$ \alpha \cong \beta' $$
  

En ramenant tous les cas à celui des angles alternes internes congruents, la démonstration est complète.

Théorème réciproque

Démonstration

On part de l'hypothèse :

$$ r // s $$

On veut montrer qu'il existe des angles alternes internes congruents ($ \alpha \cong \beta $).

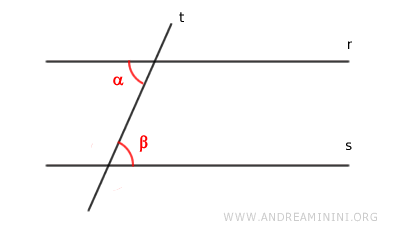
Raisonnons par l'absurde :

Si $ \alpha > \beta $, on pourrait tracer une autre droite $ r' $ telle que $ \alpha' \cong \beta $.

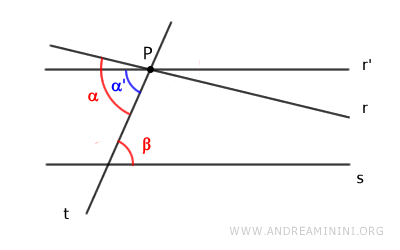
Il existerait alors deux droites parallèles à $ s $ passant par le point $ P $, ce qui contredit le postulat des parallèles.

On en conclut que deux droites parallèles $ r $ et $ s $ déterminent nécessairement des angles alternes internes congruents.

Par un raisonnement analogue, toutes les autres configurations se ramènent à celle des angles alternes internes congruents. Le théorème réciproque est ainsi établi dans tous les cas.

Observations

• Corollaire

  Si deux droites $ r $ et $ s $ sont perpendiculaires à une troisième droite $ t $, alors elles sont parallèles entre elles.
  

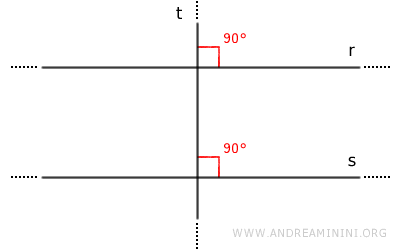
  Remarque : Des angles correspondants droits sont alors formés, ce qui satisfait directement les conditions du critère de parallélisme.

• Si une droite est perpendiculaire à l'une de deux droites parallèles, elle est perpendiculaire à l'autre.

  Démonstration :
  $$ r // s $$
  $$ t \perp s $$
  
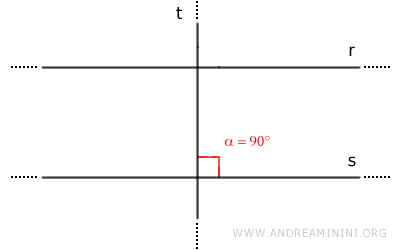
  D'après le critère de parallélisme, $ r $ et $ s $ déterminent des angles correspondants congruents. Ainsi :
  $$ \beta = 90° $$
  
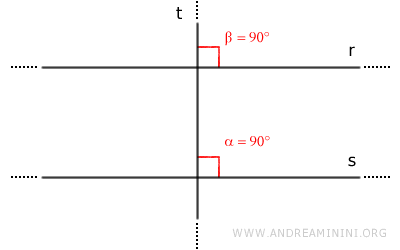
  On en déduit que $ t \perp r $.

Et ainsi de suite.