Pente (coefficient directeur) d’une droite

La pente, également appelée coefficient directeur, d’une droite écrite sous la forme $$ y = mx + b $$ mesure la façon dont la droite monte ou descend lorsque l’on se déplace le long de l’axe des abscisses. Elle est définie comme le rapport entre la variation des ordonnées et la variation des abscisses entre deux points distincts de la droite : $$ m = \frac{y_B - y_A}{x_B - x_A} $$ 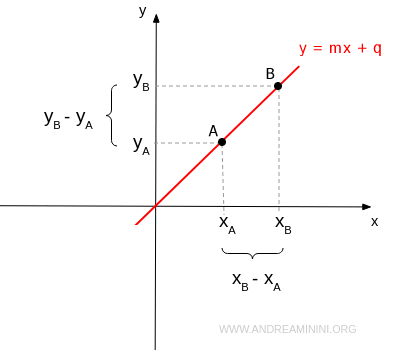définition visuelle de la pente ou du coefficient directeur d’une droite

La pente caractérise donc l’inclinaison de la droite par rapport à l’axe des abscisses.

On peut aussi l’interpréter comme l’angle α que la droite forme avec l’axe des x. Le sommet de cet angle se situe au point d’intersection entre la droite et l’axe, et ses côtés sont le demi-axe positif des x et un segment de la droite dont la composante verticale est positive ou nulle.

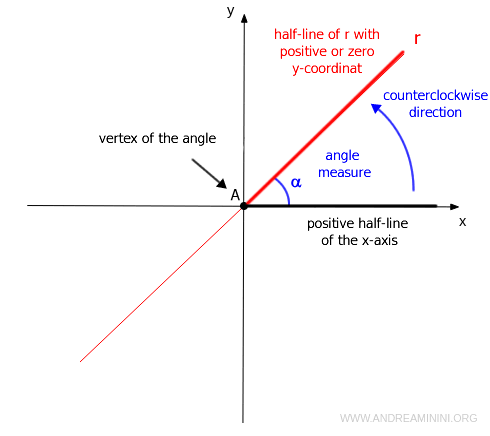
angle formé entre une droite et l’axe des abscisses

Remarque : par convention, les angles sont mesurés dans le sens antihoraire à partir du demi-axe positif des x.

Selon l’orientation de la droite, la pente, ou coefficient directeur, peut prendre différentes valeurs :

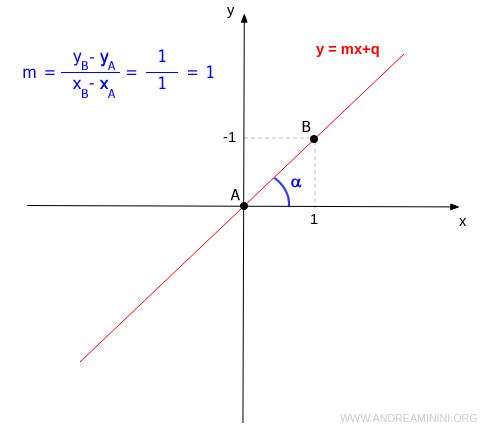
Pente positive (m > 0) : la droite est croissante. Lorsqu’on avance vers la droite, ses valeurs augmentent. Elle forme un angle aigu avec l’axe des x.
Pente négative (m < 0) : la droite est décroissante. Lorsqu’on avance vers la droite, ses valeurs diminuent. Elle forme un angle obtus avec l’axe des x.
Pente nulle (m = 0) : la droite est horizontale. Elle est parallèle à l’axe des x, ou s’y confond, et ne présente aucune inclinaison.

Remarque : la pente, ou coefficient directeur, d’une droite verticale, c’est-à-dire parallèle à l’axe des y, n’est pas définie. droite verticale sans coefficient directeur défini
En effet, le calcul fait intervenir une division par zéro : $$ m = \frac{y_B - y_A}{x_B - x_A} = \frac{y_B - y_A}{0} $$ Or une division par zéro n’a pas de sens en mathématiques, car tout nombre réel multiplié par zéro donne zéro. Il n’existe donc aucune valeur de m capable de satisfaire l’égalité $ y = m \cdot 0 $.

Pente (coefficient directeur) et tangente de l’angle

La pente $ m $, ou coefficient directeur, d’une droite est égale à la tangente de l’angle $ \alpha $ qu’elle forme avec l’axe des x : $$ m = \tan \alpha $$

Cette relation établit un lien direct entre la géométrie et la trigonométrie. Elle permet de décrire l’inclinaison d’une droite à l’aide d’un angle.

Elle est particulièrement utile pour passer d’une description algébrique à une interprétation géométrique, ou inversement :

$$ m = \tan \alpha $$

$$ \alpha = \text{arctan}(m) $$

où arctan désigne la fonction réciproque de la fonction tangente.

Remarque : l’utilisation de cette relation suppose des notions de trigonométrie et d’analyse mathématique. Elle est généralement abordée en fin de lycée ou dans les premiers cours universitaires. La démonstration est présentée dans une autre section de ce site.

Exemple

Considérons la droite $ y = 2x - 1 $. Son coefficient directeur vaut $ m = 2 $.

représentation graphique d’une droite de coefficient directeur égal à 2

Quel est l’angle $ \alpha $ que cette droite forme avec l’axe des x ?

On cherche l’angle dont la tangente est égale à 2 :

$$ \tan \alpha = 2 $$

On applique la fonction arc-tangente :

$$ \alpha = \text{arctan}(2) $$

On obtient alors :

$$ \alpha_{\text{rad}} \approx 1.107 \, \text{rad} $$

Pour exprimer cet angle en degrés, on effectue la conversion suivante : $$ \alpha = 1.107 \cdot \frac{180^\circ}{\pi} \approx 63.43^\circ $$

La droite forme donc un angle d’environ 63.43° avec l’axe des x.

angle mesuré en degrés entre la droite et l’axe des abscisses

On a ainsi déterminé l’angle $ \alpha $ à partir de la pente, ce qui illustre le lien étroit entre l’équation d’une droite et sa représentation géométrique.

Et ainsi de suite.