Les droites

Qu’est-ce qu’une droite ?

Une droite est un ensemble aligné de points qui s’étend à l’infini dans les deux directions, sans jamais se courber.

La droite est l’un des objets fondamentaux de la géométrie euclidienne.

Selon le premier postulat d’Euclide, par deux points distincts passe une et une seule droite.

On représente généralement les droites par des lettres minuscules, tandis que les points sont notés par des lettres majuscules.

Remarque. On en déduit qu’une droite ne peut jamais être courbe, car si l’on considère deux paires de points distincts du plan (A, B) et (B, C), ils n’appartiendront à une même droite que s’ils sont parfaitement alignés.

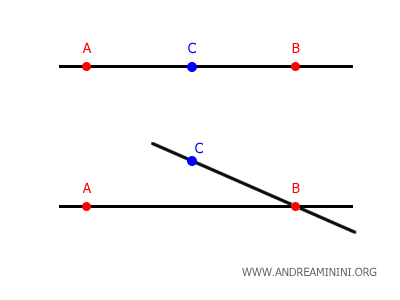
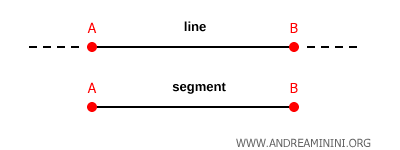
Le deuxième postulat d’Euclide précise qu’une droite est un segment que l’on peut prolonger indéfiniment dans les deux directions.

Autrement dit, une droite n’a ni origine ni extrémité.

Remarque. Cela distingue la droite du segment, qui possède lui deux extrémités : un point de départ et un point d’arrivée.

Entre deux points quelconques d’une droite, il existe toujours au moins un point intermédiaire.

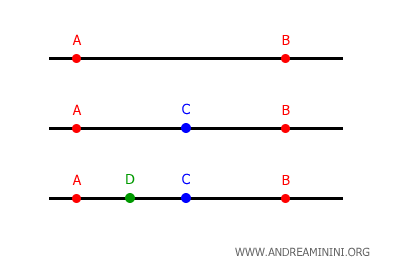
C’est pourquoi une droite est considérée comme un ensemble dense.

Remarque. Il existe une correspondance biunivoque entre les points d’une droite et l’ensemble des nombres réels : ces deux ensembles sont infinis et de même densité.

De nombreuses propriétés des droites découlent directement des deux premiers postulats d’Euclide.

Lorsque plusieurs droites passent par un même point, on parle de droites concourantes ou de droites sécantes.

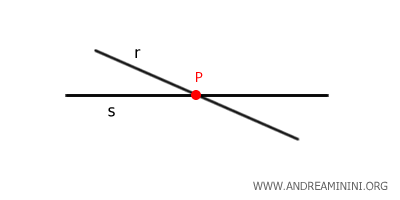
Un nombre infini de droites peuvent passer par un même point.

L’ensemble des droites passant par un même point est appelé un faisceau de droites.

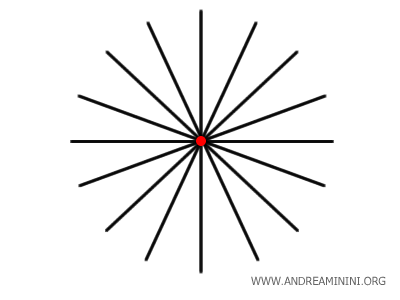
Remarque. Une droite étant un ensemble de points, elle contient nécessairement au moins un point. Or, pour définir une droite, il faut au minimum deux points distincts : on en déduit qu’une infinité de droites passent par tout point donné.

Un plan contient une infinité de points et, par conséquent, une infinité de droites.

Pour définir un plan, il est nécessaire de spécifier au moins trois points non alignés.

Dans l’espace à trois dimensions, on peut définir une droite comme l’intersection de deux plans.

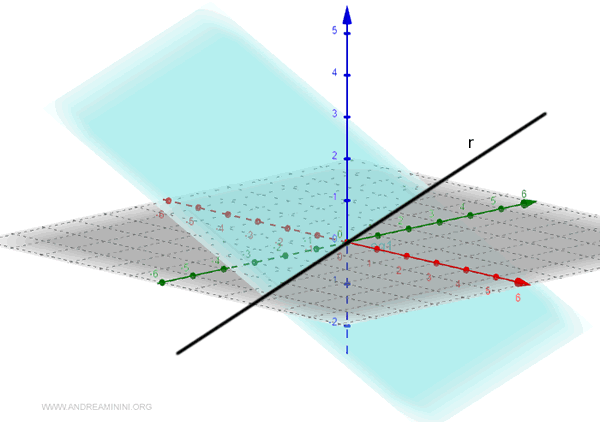
Remarque. Cette idée constitue une version simplifiée d’un concept beaucoup plus général, qui peut être étendu aux espaces de dimension supérieure en mathématiques avancées.

Sur une droite, il est toujours possible de définir un sens d’orientation.

Une droite ainsi orientée est appelée une droite orientée.

Dans le plan cartésien, une droite peut être définie par une équation linéaire :

$$ y = mx + b $$

Où :

• "y" est la coordonnée verticale (ordonnée) de tout point de la droite ;
• "x" est la coordonnée horizontale (abscisse) du point ;
• "m" représente la pente de la droite, c’est-à-dire son inclinaison (m = y/x) ;
• "b" est l’ordonnée à l’origine, c’est-à-dire le point où la droite coupe l’axe des ordonnées (lorsque x = 0).

Graphiquement, l’équation d’une droite dans le plan cartésien se représente ainsi :

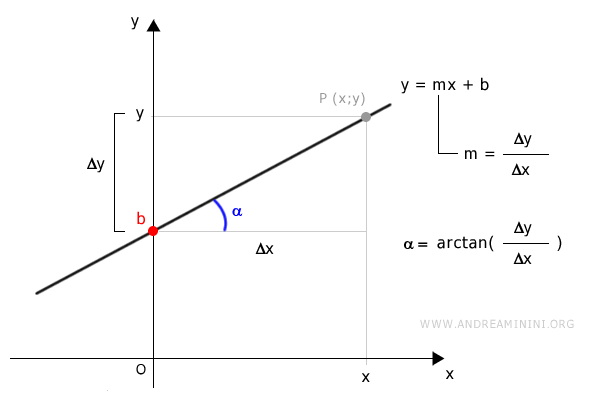
Étant donné deux points quelconques d’une droite, il est toujours possible de retrouver l’équation de cette droite en utilisant la formule de la pente et l’équation correspondante.

Et ainsi de suite.