Droite perpendiculaire à un plan

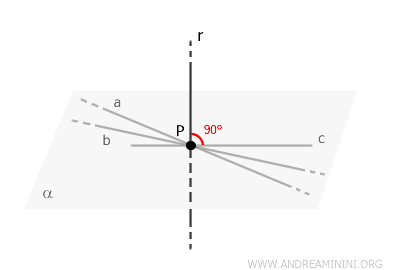
Une droite \( r \) est dite perpendiculaire à un plan \( \alpha \) lorsqu'elle coupe ce plan et qu'elle est perpendiculaire à toutes les droites qui y sont contenues.

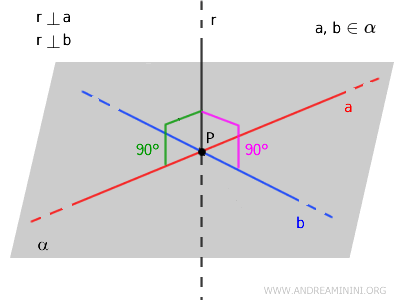
La perpendicularité d'une droite à un plan repose sur deux conditions précises, qui doivent être vérifiées simultanément :

• La droite \( r \) coupe le plan \( \alpha \) en un point unique \( P \), appartenant au plan.
• La droite \( r \) est perpendiculaire à toutes les droites du plan \( \alpha \) passant par le point d'intersection \( P \).

Remarque : Une droite qui coupe un plan en un point unique sans lui être perpendiculaire est appelée droite oblique au plan.

Observations complémentaires

Les propriétés suivantes permettent de mieux comprendre les relations de perpendicularité entre droites et plans en géométrie de l'espace.

• Théorème des trois perpendiculaires
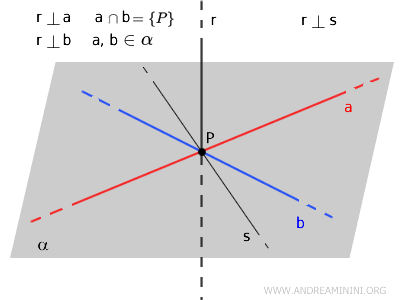
  À partir d'un point \( P \) situé sur une droite \( r \), on considère deux droites distinctes \( a \) et \( b \), toutes deux perpendiculaires à \( r \). La droite \( r \) est alors perpendiculaire à toute droite \( s \) passant par \( P \) et appartenant au plan \( \alpha \) déterminé par \( a \) et \( b \).
  
• Théorème des droites perpendiculaires à une droite dans l'espace
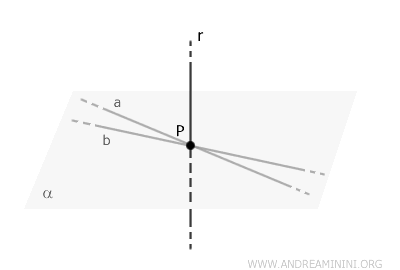
  Dans l'espace euclidien, toute droite perpendiculaire à une droite donnée \( r \) et passant par un point \( P \) appartenant à \( r \) est contenue dans un même plan.
  
• Théorème des trois perpendiculaires
  Soit une droite \( r \) perpendiculaire à un plan \( \alpha \). À partir du pied de la perpendiculaire \( H \), on trace une droite \( t \) perpendiculaire à une droite \( s \) contenue dans le plan \( \alpha \). La droite \( s \) est alors perpendiculaire au plan \( \beta \), défini par les droites \( r \) et \( t \).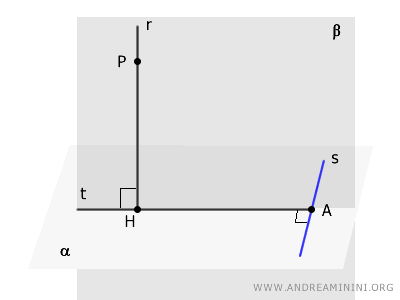

  

• Théorème de la droite perpendiculaire à un plan
  Par tout point \( P \) appartenant à un plan \( \alpha \), il passe une unique droite \( r \) perpendiculaire à ce plan.
  
• Théorème des droites perpendiculaires
  Deux droites perpendiculaires à un même plan sont parallèles entre elles.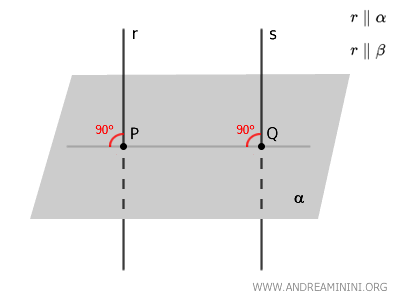

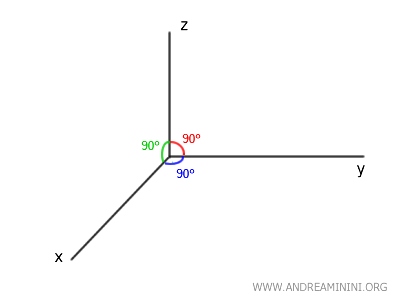
  Remarque : En géométrie de l'espace, l'affirmation selon laquelle deux droites perpendiculaires à une même droite seraient parallèles est fausse. Cette propriété ne vaut qu'en géométrie plane. Ainsi, les axes \(x\), \(y\) et \(z\) d'un repère cartésien orthonormé sont deux à deux perpendiculaires (\( x \perp y \), \( x \perp z \), \( y \perp z \)), sans être parallèles entre eux.
  

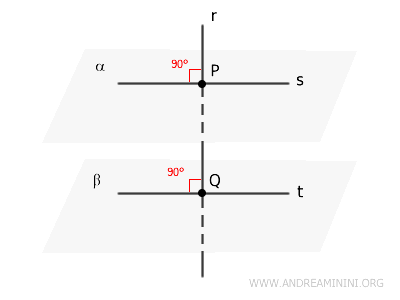
• Théorème de la droite perpendiculaire à deux plans
  Lorsqu'une droite est perpendiculaire à deux plans distincts en deux points différents de son parcours, ces deux plans sont nécessairement parallèles.
  

Et ainsi de suite.