Théorème de la droite perpendiculaire à deux plans

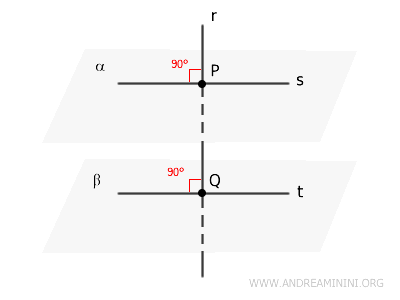
Si une droite $ r $ est perpendiculaire à deux plans $ \alpha $ et $ \beta $ en deux points distincts $ P $ et $ Q $ situés sur cette droite, alors les plans $ \alpha $ et $ \beta $ sont parallèles, c'est-à-dire $ \alpha \parallel \beta $.
schéma illustrant une droite perpendiculaire à deux plans parallèles

Ce résultat est un théorème classique de géométrie de l'espace. Il permet de comprendre et d'identifier rapidement des situations de parallélisme entre plans à partir de propriétés d'orthogonalité, ce qui en fait un outil très utile dans l'analyse géométrique en trois dimensions.

Démonstration

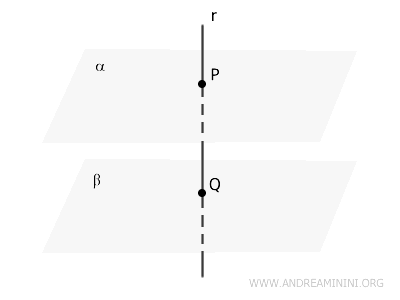
Considérons une droite $ r $ qui coupe les plans $ \alpha $ et $ \beta $ respectivement aux points $ P $ et $ Q $.

Par hypothèse, la droite $ r $ est perpendiculaire au plan $ \alpha $ et également perpendiculaire au plan $ \beta $.

exemple d'une droite perpendiculaire à un plan dans l'espace

Autrement dit, la droite $ r $ forme un angle droit avec toute droite contenue dans le plan $ \alpha $ passant par le point $ P $, ainsi qu'avec toute droite contenue dans le plan $ \beta $ passant par le point $ Q $.

Choisissons alors une droite $ s $, située dans le plan $ \alpha $ et passant par $ P $, et une droite $ t $, située dans le plan $ \beta $ et passant par $ Q $.

illustration de la construction des droites dans chaque plan

Puisque la droite $ r $ est perpendiculaire au plan $ \alpha $, elle est nécessairement perpendiculaire à la droite $ s $.

De manière analogue, la droite $ r $ est perpendiculaire à la droite $ t $.

Supposons maintenant, par raisonnement par l'absurde, que les plans $ \alpha $ et $ \beta $ ne soient pas parallèles.

Dans ce cas, ils se couperaient suivant une droite $ u $, commune aux deux plans.

Comme la droite $ u $ est contenue dans le plan $ \alpha $, et que la droite $ r $ est perpendiculaire à toutes les droites du plan $ \alpha $ passant par $ P $, la droite $ r $ serait en particulier perpendiculaire à $ u $.

$$ u \subset \alpha $$

De la même façon, la droite $ u $ étant contenue dans le plan $ \beta $, et la droite $ r $ étant perpendiculaire à toutes les droites de ce plan passant par $ Q $, la droite $ r $ serait également perpendiculaire à $ u $.

$$ u \subset \beta $$

On aboutit alors à une situation impossible. Une même droite $ r $ ne peut pas être perpendiculaire à une même droite $ u $ en deux points distincts $ P $ et $ Q $, car cela contredit le principe d'unicité de la perpendiculaire menée d'un point à une droite.

L'hypothèse selon laquelle les plans $ \alpha $ et $ \beta $ ne seraient pas parallèles conduit donc à une contradiction.

On en déduit que les plans $ \alpha $ et $ \beta $ sont nécessairement parallèles.

Démonstration alternative

On peut également démontrer ce théorème à l'aide des vecteurs.

Considérons une droite $ r $ perpendiculaire au plan $ \alpha $ au point $ P $.

Le fait que la droite $ r $ soit perpendiculaire au plan $ \alpha $ implique que son vecteur directeur, noté $ \vec{v} $, est un vecteur normal au plan $ \alpha $.

Cela signifie que le vecteur $ \vec{v} $ est orthogonal à tout vecteur contenu dans le plan $ \alpha $.

De la même manière, puisque la droite $ r $ est également perpendiculaire au plan $ \beta $ au point $ Q $, le vecteur $ \vec{v} $ est aussi un vecteur normal au plan $ \beta $.

Le vecteur $ \vec{v} $ est donc un vecteur normal commun aux deux plans. Les plans $ \alpha $ et $ \beta $ possèdent ainsi des vecteurs normaux parallèles.

Or, deux plans dont les vecteurs normaux sont parallèles sont nécessairement parallèles entre eux. On conclut donc que les plans $ \alpha $ et $ \beta $ sont parallèles.

Le théorème est ainsi établi de façon claire et rigoureuse.