Droites parallèles

Deux droites sont dites parallèles lorsqu'elles ne se rencontrent en aucun point ou lorsqu'elles coïncident en tous leurs points.

On utilise les symboles // ou || pour indiquer que deux droites sont parallèles.

$$ r // s $$ $$ r \parallel s $$

La région comprise entre deux droites parallèles s'appelle une bande ou une zone.

La distance minimale entre un point quelconque d'une droite et l'autre droite est appelée hauteur de la bande ou, de façon équivalente, distance entre deux droites parallèles.

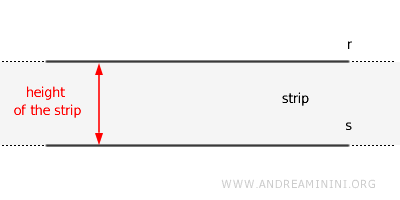
Cette hauteur correspond à la distance perpendiculaire entre les deux droites. Elle est constante en tout point de la bande.

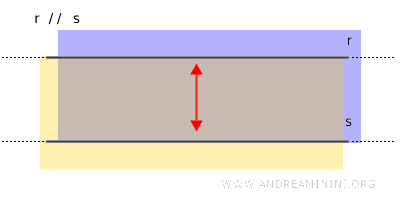
Remarque. La région comprise entre deux droites parallèles distinctes $ r $ et $ s $ peut aussi être décrite comme l'intersection du demi-plan délimité par $ r $ contenant $ s $ et du demi-plan délimité par $ s $ contenant $ r $.

Cinquième postulat d'Euclide

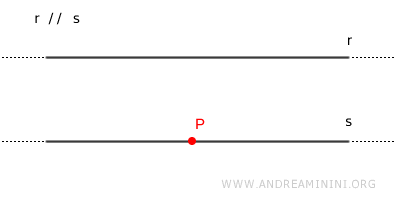
Étant donné un point $ P $ n'appartenant pas à une droite $ r $, il existe une unique droite $ s $ telle que $ s \parallel r $.

Le cinquième postulat d'Euclide, appelé postulat des parallèles, est sans doute le plus célèbre et le plus discuté de l'ensemble de ses axiomes.

Contrairement aux quatre autres, il ne découle pas immédiatement de l'intuition géométrique et ne peut pas être démontré à partir des axiomes précédents.

Plus précisément, on peut établir que, par un point extérieur à une droite $ r $, passe au moins une droite parallèle à celle-ci. En revanche, il est impossible de démontrer que cette droite est unique.

Conséquences du postulat

De ce postulat découlent plusieurs propriétés fondamentales de la géométrie euclidienne, en particulier celles qui concernent les droites parallèles.

• Théorème de transitivité du parallélisme
  Si deux droites $a$ et $b$ sont parallèles à une troisième droite $c$, alors elles sont parallèles entre elles : $$ a \parallel c \ , \ b \parallel c \ \Rightarrow  \ a \parallel b $$

  Démonstration. Raisonnons par l'absurde. Supposons que $a$ et $b$ soient parallèles à $c$, mais qu'elles ne soient pas parallèles entre elles : $$ a \parallel c $$ $$ b \parallel c $$ Si $a$ et $b$ n'étaient pas parallèles, elles se couperaient en un point $P$.
  
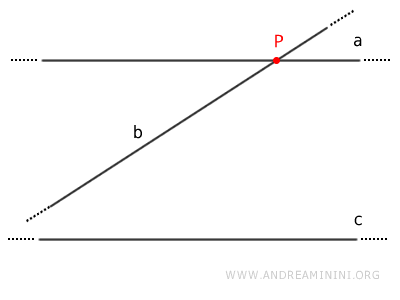
  Or, puisque $a$ et $b$ sont toutes deux parallèles à $c$, il existerait alors, par le point $P$, deux droites distinctes parallèles à $c$. Cela contredit le postulat des parallèles. L'hypothèse initiale est donc fausse, et sa négation est vraie : les droites $a$ et $b$, en plus d'être parallèles à $c$, sont également parallèles entre elles (a // b).

• Le parallélisme comme relation d'équivalence
  L'ensemble de toutes les droites parallèles à une droite donnée $r$ constitue une direction. Cet ensemble forme une classe d'équivalence, car toutes les droites qui le composent sont mutuellement parallèles et constituent un faisceau de droites. Le parallélisme définit ainsi une relation d'équivalence, car il vérifie les trois propriétés fondamentales suivantes.
  • Réflexivité
    Toute droite est parallèle à elle-même. $$ r \parallel r $$

    Remarque. Cette propriété est contenue implicitement dans la définition même du parallélisme.

  • Symétrie
    Si une droite $r$ est parallèle à une droite $s$, alors $s$ est également parallèle à $r$. $$ r \parallel s $$

    Remarque. Cette propriété découle directement du caractère symétrique de la relation.

  • Transitivité
    Si $r$ est parallèle à $s$ et si $s$ est parallèle à $p$, alors $r$ est parallèle à $p$. $$ r \parallel s \ , \ s \parallel p \ \Rightarrow r \parallel p $$

    Remarque. Cette propriété repose sur le théorème selon lequel deux droites parallèles à une même droite sont parallèles entre elles.

• Théorème de la droite sécante à un faisceau de parallèles
  Si une droite $ r $ coupe une droite $ a $ appartenant à un faisceau impropre de droites parallèles $ a \parallel b \parallel c \dots $, alors elle coupe également toutes les autres droites du faisceau.
  

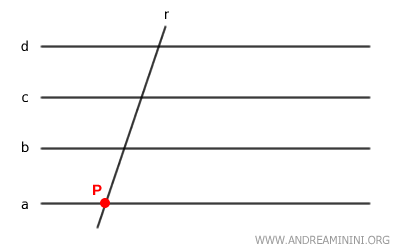
  Démonstration. Considérons un faisceau impropre de droites parallèles : $$ a \parallel b \parallel c \parallel \dots $$ et une droite $ r $ qui coupe $ a $ en un point $ P $ : $$ r \cap a = \{ P \} $$ Nous voulons montrer que $ r $ coupe également toutes les autres droites du faisceau. Supposons le contraire, c'est-à-dire que $ r $ ne coupe pas l'une d'entre elles, par exemple $ b $ : $$ r \cap b = \emptyset $$ Cela signifierait que $ r $ est parallèle à $ b $ : $$ r \parallel b $$ Or, puisque $ b \parallel a $, la transitivité implique : $$ r \parallel a $$ ce qui contredit le fait que $ r $ et $ a $ se coupent au point $ P $. L'hypothèse $$ r \cap b = \emptyset $$ est donc fausse, et l'on doit avoir : $$ r \cap b \ne \emptyset $$ Ce raisonnement s'applique à toute droite du faisceau. Ainsi, $ r $ coupe nécessairement toutes les droites de l'ensemble.

Condition nécessaire et suffisante pour que deux droites soient parallèles

Pour que deux droites soient parallèles, deux conditions fondamentales doivent être réunies. Ces conditions permettent de distinguer clairement les droites parallèles de toutes les autres configurations possibles.

Coplanarité

Deux droites parallèles doivent appartenir à un même plan, c'est-à-dire être coplanaires.

Si deux droites ne se trouvent pas dans un même plan, elles ne peuvent pas être parallèles.

La coplanarité constitue donc une condition nécessaire, mais à elle seule insuffisante.

Par exemple, dans l'espace tridimensionnel, deux droites situées dans des plans différents sont dites gauches. Par définition, elles ne peuvent jamais être parallèles.

Absence d'intersection

Pour que deux droites soient parallèles, elles doivent être coplanaires et ne se couper en aucun point.

Autrement dit, elles doivent appartenir au même plan sans avoir de point commun.

Cette condition est à la fois nécessaire et suffisante pour caractériser le parallélisme.

Deux droites contenues dans un même plan et ne se coupant pas sont donc, par définition, parallèles.

Théorème des droites parallèles

Ce résultat est connu sous le nom de critère de parallélisme.

La réciproque est également vraie : si deux droites sont parallèles, toute sécante qui les coupe engendre des angles alternes égaux, des angles correspondants égaux et des angles conjugués supplémentaires.

Définition alternative

Deux droites non verticales sont parallèles si et seulement si elles ont la même pente.

Autrement dit, elles présentent la même inclinaison par rapport à l'axe des abscisses.

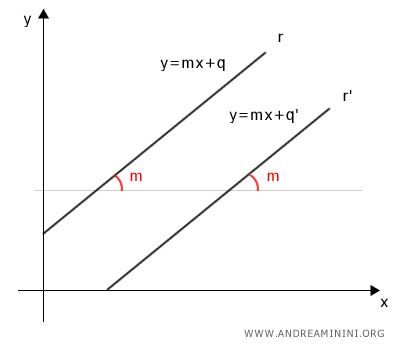
Les droites verticales, parallèles à l'axe des ordonnées, constituent un cas particulier, car leur pente n'est pas définie.

Théorème réciproque. Si deux droites ont la même pente (m = m'), alors elles sont parallèles.

Exemple avec démonstration

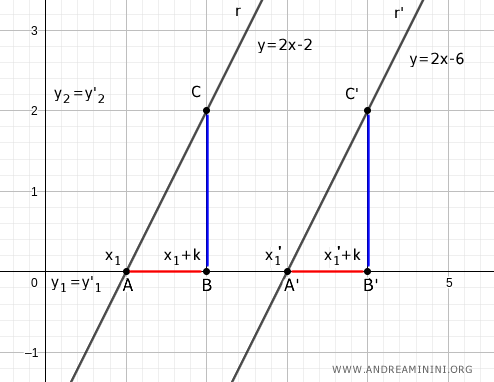
Considérons deux droites parallèles : r : y = 2x - 2 et r' : y = 2x - 6.

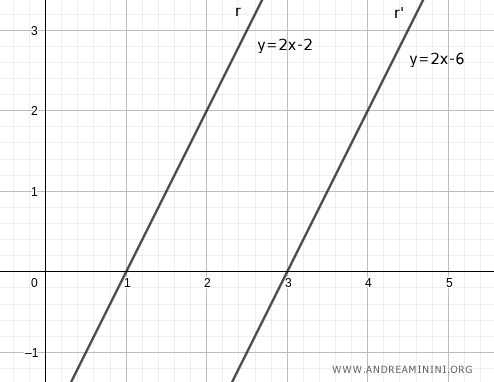
Soient x₁ et x₁' les abscisses des points d'intersection de ces droites avec l'axe des abscisses.

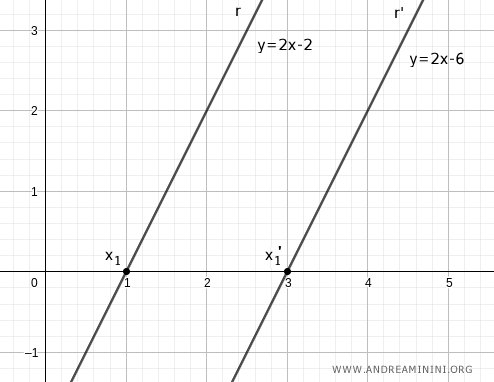
Choisissons ensuite deux nouveaux points en ajoutant une constante k à x₁ et x₁'. Par exemple, pour k = 1 :

$$ x_2 = x_1 + k \qquad x_2' = x_1' + k $$

Les segments x₁x₂ et x₁'x₂' ont alors la même longueur.

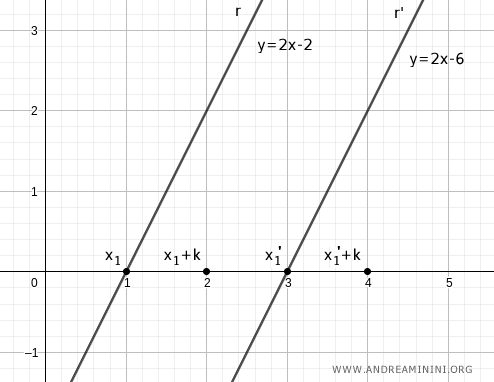
À partir de ces nouveaux points, on trace des perpendiculaires qui rencontrent les droites r et r'.

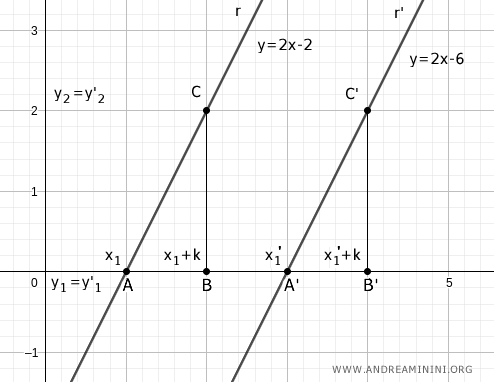
On obtient ainsi deux triangles rectangles, notés ABC et A'B'C'.

Ils possèdent un angle droit commun : α = α'.

D'après le théorème du parallélisme, les angles β = β' sont également égaux, car ils sont correspondants et déterminés par une même sécante, l'axe des abscisses.

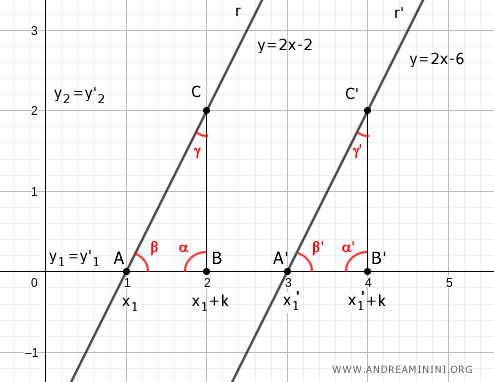
Selon le deuxième critère de congruence des triangles, les triangles ABC et A'B'C' sont congruents, car ils possèdent un côté égal et deux angles adjacents égaux.

Remarque. Les deux triangles étant rectangles, ils partagent un angle droit, et les angles formés par la sécante sont également égaux. Le troisième angle est donc identique (γ = γ').

Comme les triangles sont congruents, leurs côtés correspondants sont égaux :

$$ \overline{AB} \cong \overline{A'B'} \qquad \overline{BC} \cong \overline{B'C'} $$

Or, comme AB = x₂ - x₁ et A'B' = x₂' - x₁', et puisque les segments verticaux sont également égaux, on obtient :

$$ \frac{y_2 - y_1}{x_2 - x_1} = \frac{y'_2 - y'_1}{x'_2 - x'_1} $$

Les pentes sont donc égales :

$$ m = m' $$

Démonstration du théorème réciproque. En partant de l'égalité m = m', on montre que les triangles construits sont congruents et que, par conséquent, les droites sont parallèles.

Si m = m' et si l'on sait que m = BC / AB et m' = B'C' / A'B', alors : $$ \frac{BC}{AB} = \frac{B'C'}{A'B'} $$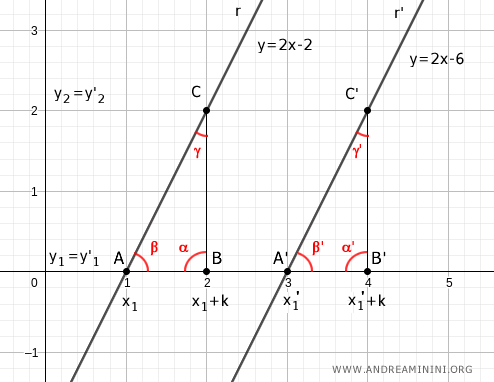
Comme AB ≅ A'B' et BC ≅ B'C', et que l'angle compris est droit, les triangles sont congruents selon le premier critère de congruence. On en déduit que les angles β et β' sont égaux et que les droites r et r' sont parallèles : r // r'.

Condition de parallélisme pour des droites sous forme implicite

Soient deux droites $ r $ et $ s $ définies par les équations implicites suivantes : $$ r : ax + by + c = 0 $$ $$ s : a'x + b'y + c' = 0 $$ Alors $ r // s $ si et seulement si la condition suivante est vérifiée : $$ ab' - a'b = 0 $$ Cette condition peut également s'écrire : $$ \frac{a}{a'} = \frac{b}{b'} $$

On parle alors de condition de parallélisme entre droites.

Exemple

Considérons les deux droites suivantes :

$$ r : 2x + 3y + 1 = 0 $$

$$ s : 4x + 6y - 8 = 0 $$

Vérifions si elles satisfont la condition de parallélisme :

$$ ab' - a'b = 2 \cdot 6 - 4 \cdot 3 = 12 - 12 = 0 $$

Comme l'égalité est vérifiée, on conclut que les deux droites sont parallèles : $ r // s $.

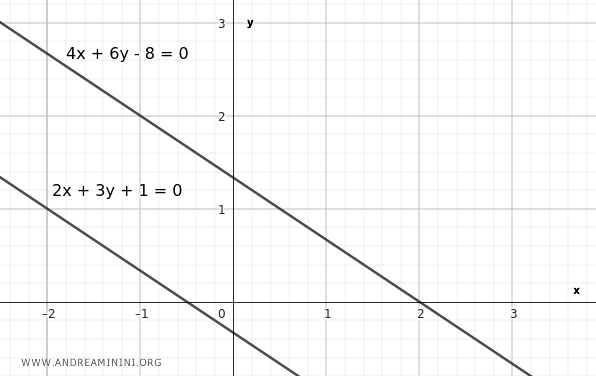
Démonstration

Soient deux droites parallèles $ r // s $ définies par :

$$ r : ax + by + c = 0 \qquad s : a'x + b'y + c' = 0 $$

Leurs pentes respectives sont :

$$ m = -\frac{a}{b} \qquad m' = -\frac{a'}{b'} $$

Puisque $ r $ et $ s $ sont parallèles, on a :

$$ m = m' $$

D'où :

$$ -\frac{a}{b} = -\frac{a'}{b'} \Rightarrow \frac{a}{b} = \frac{a'}{b'} \Rightarrow ab' = a'b $$

Ce qui achève la démonstration.

Comment déterminer si deux droites parallèles sont distinctes ou confondues

Pour établir si deux droites parallèles sont distinctes ou si elles coïncident, il est nécessaire d'examiner non seulement leur direction, mais aussi leur position dans le plan. Cette distinction repose sur des critères simples, issus de l'étude des équations cartésiennes des droites.

Deux droites sont dites parallèles distinctes lorsqu'elles vérifient la condition de parallélisme sans satisfaire la condition de coïncidence : $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ En revanche, si les trois rapports sont égaux, les droites sont confondues, c'est-à-dire qu'elles représentent exactement la même droite : $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

Les droites parallèles distinctes comme les droites confondues satisfont toutes deux la condition de parallélisme :

$$ \frac{a}{a'} = \frac{b}{b'} $$

où \( a, b, a', b' \) sont les coefficients des variables \( x \) et \( y \) dans les équations :

$$ r : ax + by + c = 0 \qquad r' : a'x + b'y + c' = 0 $$

Les droites confondues constituent donc un cas particulier du parallélisme : elles possèdent la même pente et partagent l'ensemble de leurs points.

Pour distinguer deux droites parallèles distinctes de deux droites confondues, il suffit d'examiner la valeur du rapport entre les termes constants \( \frac{c}{c'} \).

• Droites confondues
  Si les rapports sont tous égaux : $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$ alors les deux équations décrivent exactement la même droite.
• Droites parallèles distinctes
  Si le rapport des coefficients de \( x \) et de \( y \) est le même, mais différent de celui des constantes : $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ alors les droites sont parallèles sans être confondues.

Exemple

Considérons les équations suivantes :

$$ r : 2x + 3y + 6 = 0 \qquad r' : 4x + 6y + 12 = 0 $$

Vérifions d'abord la condition de parallélisme :

$$ \frac{2}{4} = \frac{3}{6} = \frac{1}{2} $$

La condition est satisfaite : les droites sont parallèles.

Vérifions maintenant la condition de coïncidence :

$$ \frac{6}{12} = \frac{1}{2} $$

Les trois rapports étant égaux, les droites sont confondues :

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

Les deux équations représentent donc une seule et même droite.

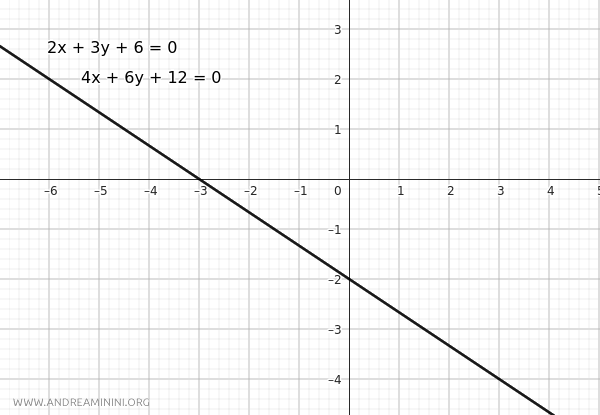
Cette méthode permet d'identifier la relation entre deux droites sans résoudre de système d'équations, simplement en comparant les rapports de leurs coefficients.

Exemple de droites parallèles distinctes.
Considérons maintenant : $$ r : 2x + 3y + 6 = 0 \qquad r' : 4x + 6y + 3 = 0 $$ La condition de parallélisme est vérifiée : $$ \frac{2}{4} = \frac{3}{6} = \frac{1}{2} $$ En revanche, la condition de coïncidence ne l'est pas : $$ \frac{6}{3} = 2 \ne \frac{1}{2} $$ On a donc : $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ Les deux droites sont parallèles mais distinctes.

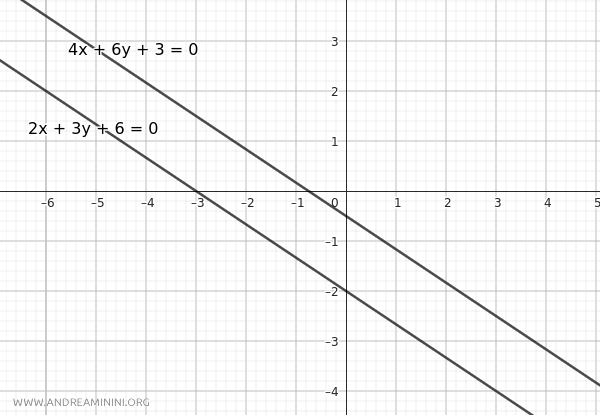
Observations géométriques importantes

• La distance entre deux droites parallèles est constante
  Si l'on trace plusieurs segments perpendiculaires entre deux droites parallèles, leur longueur est toujours la même.
  
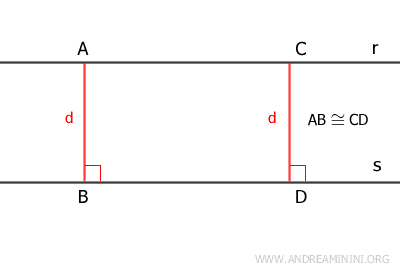
  Autrement dit, la distance entre deux droites parallèles ne dépend pas du point choisi.

  Démonstration. Soient \( r // s \) et deux perpendiculaires \( AB \) et \( CD \) tracées entre elles. Le quadrilatère \( ABCD \) est un rectangle. Or, dans un rectangle, les côtés opposés sont égaux, donc \( AB \cong CD \). La distance est donc constante.
  
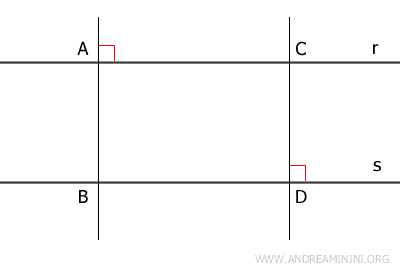
  Autre démonstration. Soient \( A \) et \( C \) deux points de la droite \( r \). On trace les perpendiculaires à \( s \) passant par ces points et on obtient les segments \( AB \) et \( CD \). Les triangles \( ABD \) et \( ACD \) sont congruents par le critère ASA, d'où \( AB = CD \).

• Deux droites perpendiculaires à une même droite sont parallèles
  Si deux droites \( r \) et \( s \) sont toutes deux perpendiculaires à une même droite \( t \), alors elles sont parallèles entre elles.
  

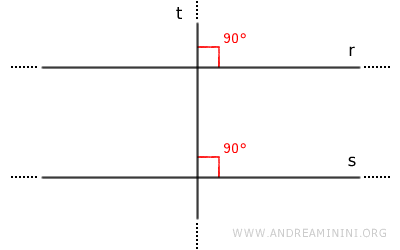
  Démonstration. Si \( r \) et \( s \) se coupaient, il existerait deux droites distinctes passant par un même point et perpendiculaires à \( t \), ce qui est impossible. On en déduit que \( r // s \).

• Les parallèles à deux droites sécantes se coupent
  

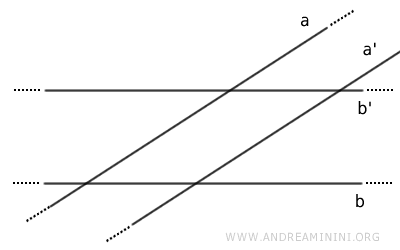
  Démonstration. Supposons que \( a \) et \( b \) soient sécantes, et que leurs parallèles respectives \( a' \) et \( b' \) soient parallèles entre elles. On aurait alors : $$ a \parallel a' \qquad b \parallel b' \qquad a' \parallel b' $$ ce qui impliquerait, par transitivité, que \( a \parallel b \), contradiction. Ainsi, \( a' \) et \( b' \) se coupent nécessairement.

• Postulat des parallèles
  Étant donné un point \( P \) extérieur à une droite \( r \), il existe une unique droite passant par \( P \) et parallèle à \( r \).
  
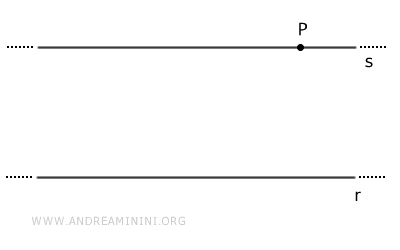
• Une droite perpendiculaire à une droite parallèle est aussi perpendiculaire à toute droite parallèle
  Si \( t \perp s \) et \( s // r \), alors \( t \perp r \).

  Démonstration. Si \( t \) est perpendiculaire à \( s \), l'angle formé est droit. Comme \( s \) et \( r \) sont parallèles, les angles correspondants formés avec \( t \) sont égaux. Il s'ensuit que \( t \perp r \).