Postulat des parallèles

Le postulat des parallèles, aussi appelé cinquième postulat d'Euclide, occupe une place centrale en géométrie. Il peut être formulé ainsi :

Étant donnée une droite r et un point P situé hors de cette droite, il existe une unique droite parallèle à r passant par le point P.

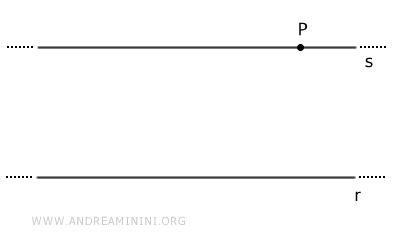
On parle de postulat parce que cette unicité ne se déduit pas des autres axiomes ni des propriétés élémentaires des droites. Elle est admise comme un principe de base de la géométrie euclidienne.

En revanche, l'existence d'une droite parallèle à r passant par P peut être établie à l'aide du théorème des droites parallèles, en identifiant une paire d'angles alternes-internes congruents α≅β.

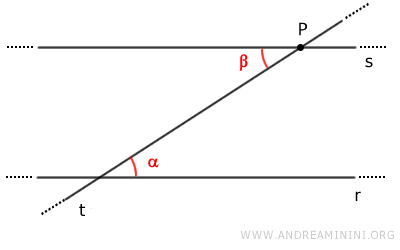
Note : Ce principe est traditionnellement désigné comme le cinquième postulat d'Euclide, bien que sa formulation courante soit généralement attribuée à Proclus, mathématicien et philosophe byzantin du Ve siècle apr. J.-C.

La démonstration

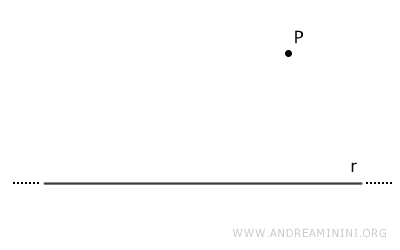
Considérons une droite r et un point P du plan, situé à l'extérieur de cette droite.

Choisissons un point P' appartenant à la droite r, puis traçons la droite t passant par P' et P.

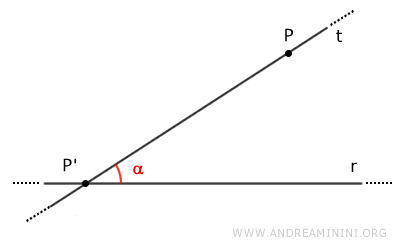
La droite t forme avec la droite r un angle intérieur, noté alpha (α).

Avec pour centre P' et pour rayon PP', traçons un arc de cercle qui coupe la droite r au point A.

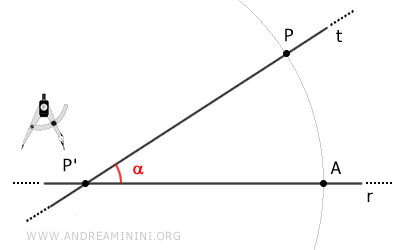
Sans modifier l'ouverture du compas, plaçons-le en P et traçons un second arc passant par P'.

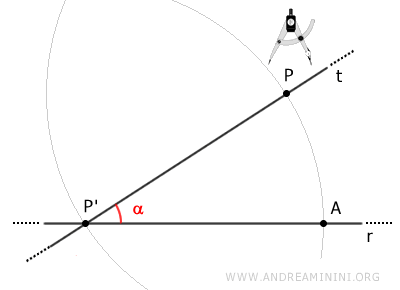
Relions alors les points A et P par le segment AP.

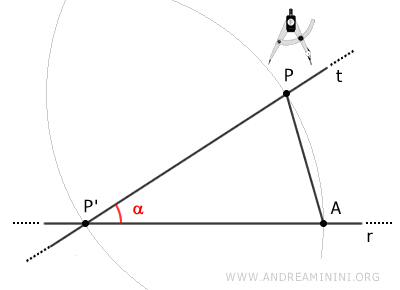
Avec pour centre P' et pour rayon AP, traçons un troisième arc qui coupe le second au point B.

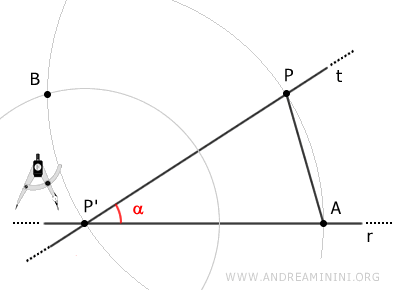
Relions ensuite les points P' et B par le segment BP'.

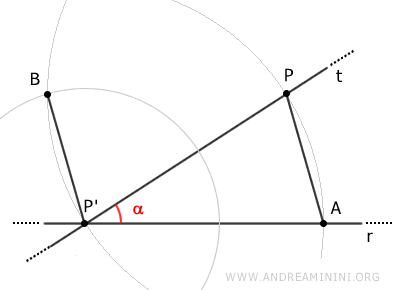
Enfin, traçons la droite s passant par les points B et P.

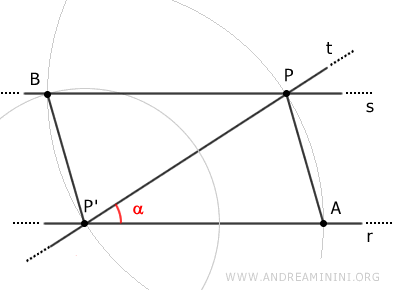
Les droites r et s déterminent alors deux triangles, notés APP' et BPP'.

D'après le troisième critère de congruence des triangles, appelé critère côté-côté-côté, ces deux triangles sont congruents, car leurs côtés correspondants ont même longueur.

$$ APP' \cong BPP' $$

La congruence des triangles implique celle de leurs angles correspondants.

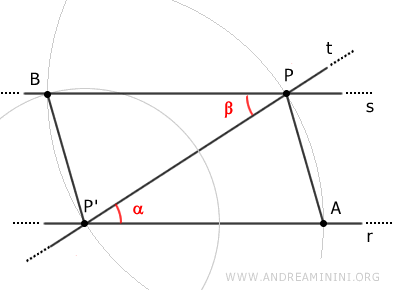
On en déduit que l'angle alpha est congruent à l'angle bêta.

$$ \alpha \cong \beta $$

Les angles alpha et bêta forment ainsi une paire d'angles alternes-internes congruents.

Conformément au théorème des droites parallèles, cette égalité d'angles implique que les droites r et s sont parallèles.

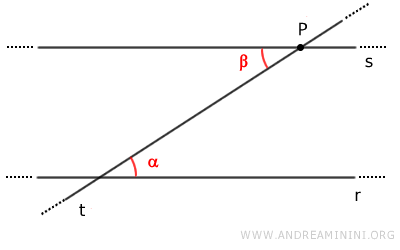
Nous avons ainsi établi l'existence d'une droite s parallèle à la droite r passant par le point P.

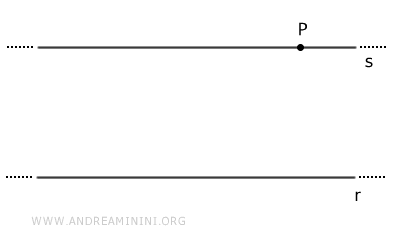
Note : L'unicité de la droite parallèle s ne peut toutefois pas être démontrée à partir des autres axiomes. Elle est donc posée comme un postulat.

Pourquoi l'unicité ne peut-elle pas être démontrée ?

Euclide avait lui-même conscience du caractère particulier de ce postulat, qu'il jugeait moins évident et moins intuitif que les autres. Il cherchait donc à en limiter l'usage, en ne l'introduisant que lorsque cela était strictement nécessaire.

Pendant des siècles, de nombreux mathématiciens ont tenté de déduire le cinquième postulat à partir des quatre premiers, sans succès. Ce postulat est indépendant. Toutes les tentatives de démonstration finissaient par faire intervenir, parfois de manière implicite, des hypothèses équivalentes à celui-ci.

Dans l'espoir de montrer qu'une seule parallèle peut passer par un point extérieur à une droite, conformément à l'intuition classique, certains chercheurs ont même proposé des formulations alternatives du postulat.

Ces démarches n'ont pas conduit à des contradictions, mais à la découverte de cadres géométriques nouveaux, parfaitement cohérents sur le plan logique.

Note : Girolamo Saccheri tenta une démonstration par l'absurde en développant une géométrie où le cinquième postulat était nié. Il espérait y mettre en évidence une incohérence, mais n'en trouva aucune.

Ces travaux ont ouvert la voie, au XIXe siècle, au développement des géométries non euclidiennes, dans lesquelles le cinquième postulat est remplacé par une hypothèse différente :

• Géométrie hyperbolique (Lobatchevski, Bolyai) : Par un point extérieur à une droite donnée passent une infinité de droites parallèles, et la somme des angles intérieurs de tout triangle est strictement inférieure à 180°.
  

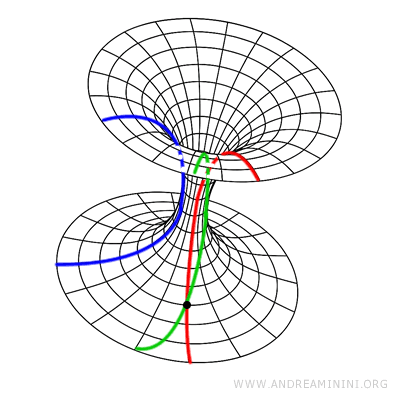
  Note : Les travaux de Saccheri, Lobatchevski et Bolyai ont été complétés par ceux de Felix Klein et d'Henri Poincaré, qui ont construit des modèles de géométrie hyperbolique à l'intérieur de la géométrie euclidienne. Ils ont ainsi montré que, si la géométrie euclidienne est cohérente, la géométrie hyperbolique l'est également. Dans le modèle de Klein, par exemple, le « plan » est représenté par l'intérieur d'un disque, et les « droites » par des cordes de ce disque.

• Géométrie elliptique (Riemann) : Il n'existe aucune droite parallèle passant par un point extérieur à une droite donnée. De plus, la somme des angles intérieurs d'un triangle est strictement supérieure à 180°. Sur une sphère, par exemple, il n'existe pas de parallèles, puisque toutes les « droites » sont des grands cercles qui se coupent nécessairement.
  

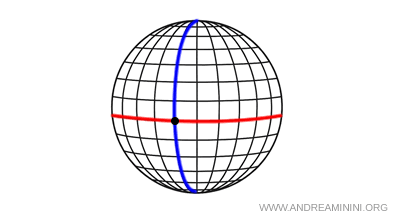
La découverte des géométries non euclidiennes constitue l'un des tournants majeurs des mathématiques du XIXe siècle.

Elle a montré que de nombreuses propriétés longtemps considérées comme universelles dépendent en réalité du cinquième postulat, et que les axiomes d'Euclide ne sont pas le seul fondement possible d'une géométrie cohérente.

Elle a également conduit à repenser la notion même d'axiome, désormais comprise non comme une vérité absolue, mais comme une hypothèse de départ définissant le cadre logique d'un système mathématique.

Au-delà des mathématiques, l'essor des géométries non euclidiennes a profondément renouvelé notre compréhension de l'espace. Il a montré que la notion d'espace n'est pas absolue, et qu'elle peut être pensée de différentes manières, toutes mathématiquement légitimes.

En définitive, le cinquième postulat nous apprend qu'il n'existe pas une unique « géométrie vraie », mais une pluralité de géométries possibles, la géométrie euclidienne n'étant qu'un cas particulier. Reste ouverte la question de savoir laquelle décrit le mieux la réalité physique. Selon la théorie de la relativité générale d'Einstein, la gravitation courbe l'espace. À proximité des trous noirs, par exemple, cette courbure devient extrême. Pour comprendre la géométrie globale de l'Univers, il est donc nécessaire de déterminer s'il est globalement plat ou courbe. Les observations actuelles suggèrent que, si une courbure existe, elle est extrêmement faible, de sorte que l'Univers apparaît presque plat.

Et l'histoire se poursuit.