La distance entre deux points
La distance est la longueur minimale du segment qui relie deux points. En géométrie analytique, la distance euclidienne entre deux points du plan se calcule à l'aide du théorème de Pythagore : $$ \overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
Dans cette expression, $(x_1, y_1)$ et $(x_2, y_2)$ représentent les coordonnées cartésiennes des points A et B.
Un exemple concret
Considérons deux points du plan dont les coordonnées cartésiennes sont :
$$ A = \begin{pmatrix} 2 \\ 4 \end{pmatrix} = (2, 4) $$
$$ B = \begin{pmatrix} 6 \\ 1 \end{pmatrix} = (6, 1) $$
La distance entre ces deux points se calcule étape par étape :
$$ \overline{AB} = \sqrt{(6-2)^2+(1-4)^2} $$
$$ \overline{AB} = \sqrt{4^2+(-3)^2} = \sqrt{16+9} = \sqrt{25} = 5 $$
Vérification avec Geogebra. La valeur obtenue correspond à celle affichée par Geogebra.
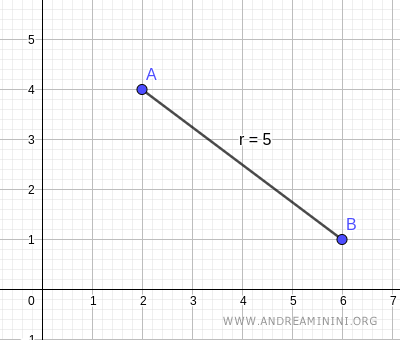
La démonstration
Considérons deux points situés dans le plan :
Le segment AB représente la distance séparant les points A et B.
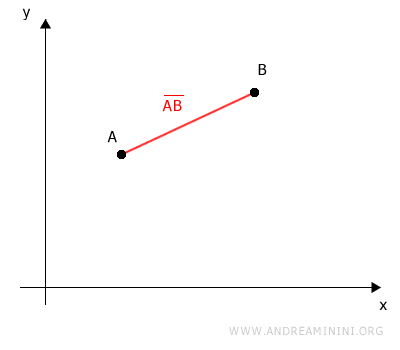
Projetons maintenant ces deux points sur les axes du repère cartésien.
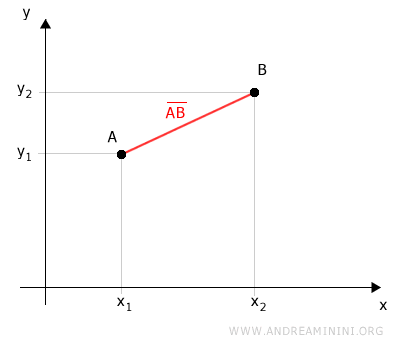
Ces projections permettent de construire un triangle rectangle ABC dans le plan.
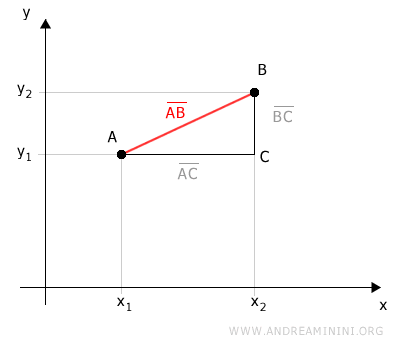
Dans ce triangle rectangle, le segment AB est l'hypoténuse.
On peut alors appliquer le théorème de Pythagore pour exprimer la longueur de AB.
$$ \overline{AB} = \sqrt{\overline{AC}^2 + \overline{BC}^2} $$
Le segment AC correspond à la projection de AB sur l'axe des abscisses.
$$ \overline{AB} = \sqrt{(x_2-x_1)^2 + \overline{BC}^2} $$
Le segment BC correspond à la projection de AB sur l'axe des ordonnées.
$$ \overline{AB} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} $$
On retrouve ainsi la formule générale de la distance entre deux points du plan.
Distance entre deux points dans l'espace
Soient deux points A $(x_A,\,y_A,\,z_A)$ et B $(x_B,\,y_B,\,z_B)$ dans l'espace cartésien. La distance $AB$ est donnée par la formule : $$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$$
Géométriquement, cette distance correspond à la longueur de la diagonale d'un parallélépipède rectangle dont les arêtes ont pour longueurs les différences absolues sur chaque axe : $|x_A-x_B|$, $|y_A-y_B|$ et $|z_A-z_B|$.
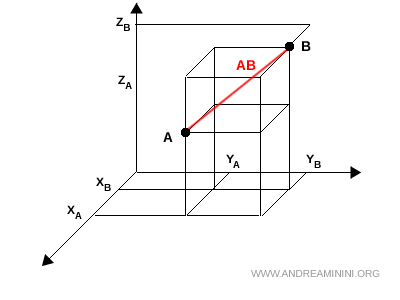
Calculer la distance entre $ A $ et $ B $ revient donc à déterminer la longueur de la diagonale $ AB $ de ce parallélépipède.
Remarque. Lorsque l'un des points coïncide avec l'origine $O(0,0,0)$, la formule se simplifie et se réduit à la norme du vecteur position de l'autre point. Ainsi, la distance du point $ A $ à l'origine $ O $ est : $$ AO=\sqrt{x_A^2+y_A^2+z_A^2} $$
Exemple
Considérons les deux points suivants dans l'espace :
$$ A(2,\,-1,\,3)$$
$$ B(-2,\,4,\,0) $$
La distance entre ces deux points se calcule pas à pas :
$$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2} $$
$$ AB=\sqrt{(2-(-2))^2+((-1)-4)^2+(3-0)^2} $$
$$ AB=\sqrt{4^2+(-5)^2+3^2} $$
$$ AB=\sqrt{16+25+9} $$
$$ AB=\sqrt{50} \approx 7.071 $$
La distance entre les deux points est donc $ \sqrt{50} $.
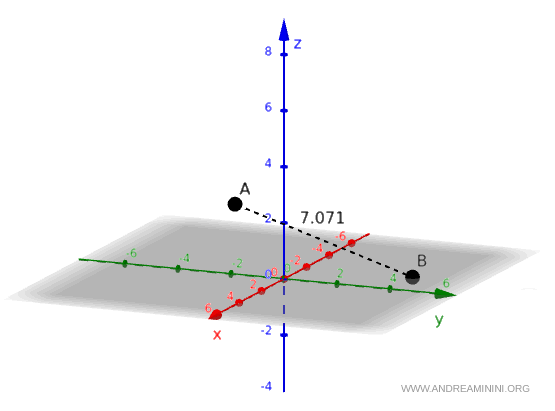
Distance à partir de coordonnées polaires
Dans le plan, la distance entre deux points peut aussi être déterminée à partir de leurs coordonnées polaires grâce à la formule suivante : $$ \overline{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
où $(r_1, \alpha_1)$ et $(r_2, \alpha_2)$ sont les coordonnées polaires des deux points considérés.
Exemple
Deux points du plan ont pour coordonnées polaires :
$$ A [ \ 4.47 \ , \ 63.43° \ ] $$
$$ B [ \ 6.08 \ , \ 9.46° \ ] $$
La situation est représentée graphiquement ci-dessous :
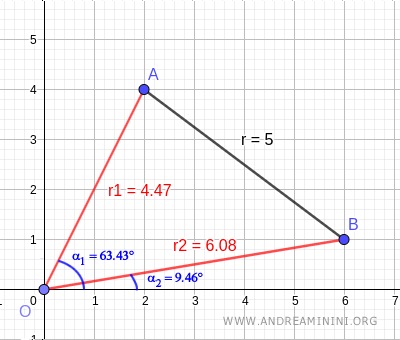
La distance entre A et B est alors donnée par :
$$ \overline{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
$$ \overline{AB} = \sqrt{(4.47)^2 + (6.08)^2 - 2 \cdot (4.47) \cdot (6.08) \cos (9.46° - 63.43°)} $$
$$ \overline{AB} = \sqrt{19.98 + 36.97 - 54.36 \cdot \cos (-53.97°)} $$
$$ \overline{AB} = \sqrt{25} = 5 $$
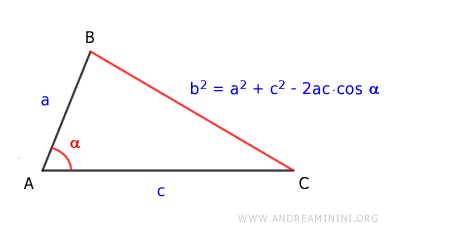
Démonstration. Cette formule résulte directement de l'application de la loi des cosinus dans un triangle.
Et ainsi de suite.