Théorème de la perpendiculaire par un point à une droite
Par tout point P du plan passe une et une seule droite perpendiculaire à une droite donnée « r ».
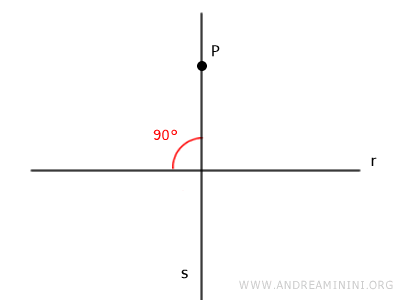
En d'autres termes, dès que l'on fixe un point P du plan et une droite r, qu'elle passe ou non par ce point, il existe une unique droite s qui passe par P et qui est perpendiculaire à r.
Le point où cette perpendiculaire rencontre la droite r est appelé le pied de la perpendiculaire.
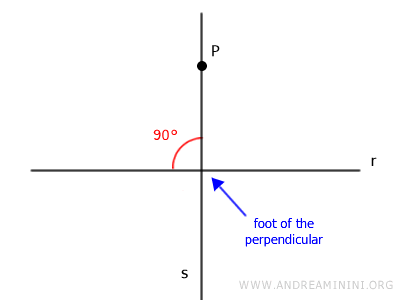
Ce résultat est souvent formulé comme le théorème d'existence et d'unicité de la perpendiculaire par un point à une droite.
Démonstration
Soit $ P $ un point du plan qui n'appartient pas à la droite $ r $. On considère la droite $ s $, perpendiculaire à $ r $, qui passe par $ P $.
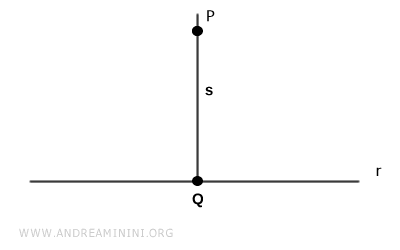
On note $ Q $ le pied de la perpendiculaire issue de $ P $ sur la droite $ r $.
Sur la droite $ r $, on choisit deux points distincts $ A $ et $ B $ placés à la même distance du point $ Q $.
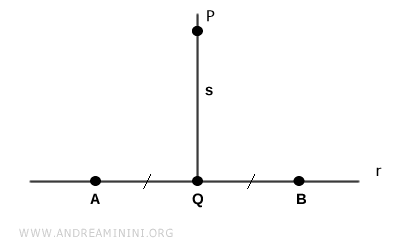
On relie ensuite ces points au point P en traçant les segments $ AP $ et $ BP $.
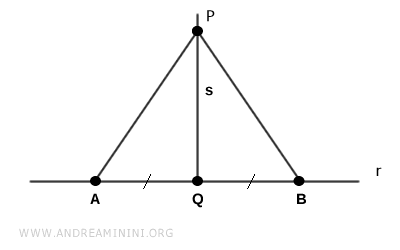
Par construction, le segment $ PQ $ est la bissectrice de l'angle $ A \hat P B $. Comme ce segment appartient à la droite $ s $, la bissectrice de l'angle est perpendiculaire à la droite $ r $.
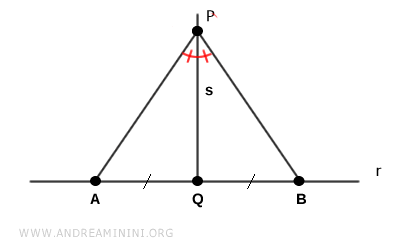
La bissectrice d'un angle étant unique, on en déduit immédiatement que la droite perpendiculaire à $ r $ passant par le point $ P $ est elle aussi unique.
Autre démonstration
Cette démonstration repose sur l'étude de deux situations distinctes.
Il convient en effet de distinguer selon que le point P appartient ou non à la droite « r ».
A] Le point P appartient à la droite (P ∈ r)
Considérons une droite r du plan et un point P situé sur cette droite.
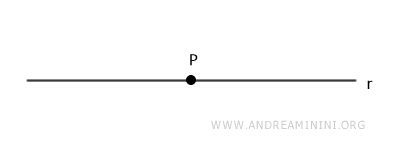
À l'aide d'un compas centré en P, on marque sur la droite deux points A et B à l'aide d'une ouverture quelconque.
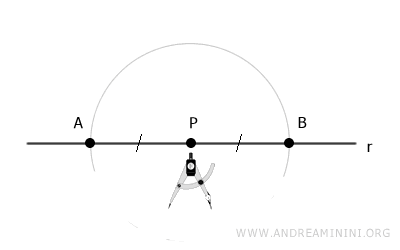
Les points A et B étant à la même distance de P, les segments AP et BP sont congruents, c'est-à-dire de même longueur.
$$ AP \cong BP $$
Il en résulte que le point P est le milieu du segment AB.
On centre ensuite le compas en A et l'on trace un arc de cercle de rayon AB.
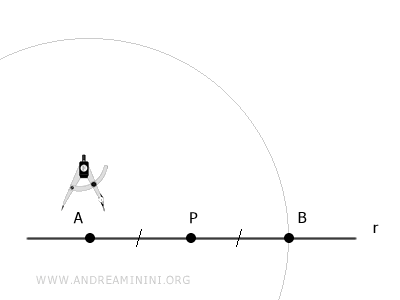
Puis, en centrant le compas en B, on trace un second arc de cercle de même rayon.
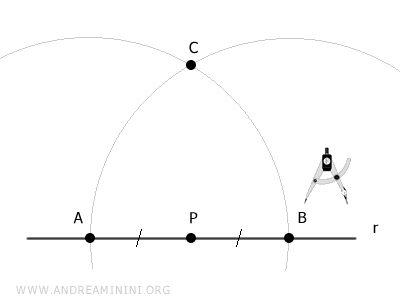
Le point d'intersection de ces deux arcs est noté C.
Remarque : Le rayon peut être choisi différent de AB, à condition qu'il soit strictement supérieur à AP, afin de garantir l'intersection des arcs.
Comme il n'existe qu'une seule droite passant par deux points distincts du plan,
il existe une unique droite s passant par les points P et C.
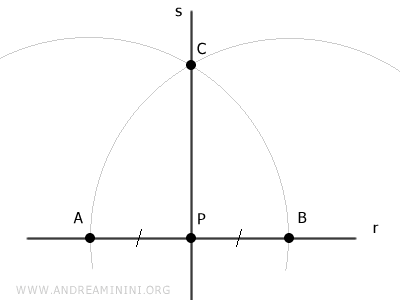
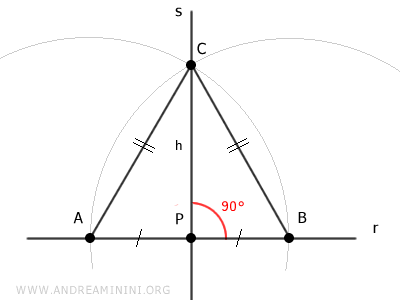
La droite s est perpendiculaire à la droite r, car le triangle ABC est un triangle isocèle, les côtés AC et BC étant congruents par construction (AC≅BC).
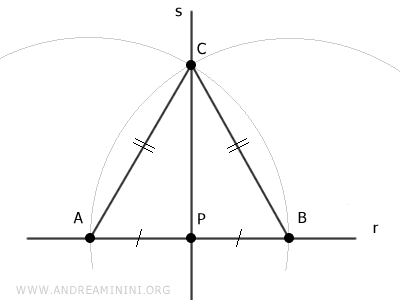
Le segment CP constitue la médiane de ce triangle, puisqu'il relie le sommet C au milieu P du côté opposé AB.
Dans un triangle isocèle, la médiane issue du sommet principal coïncide avec la hauteur. Il s'ensuit que le segment CP est perpendiculaire à la base AB.
Par conséquent, la droite s, support du segment CP, est perpendiculaire à la droite r.
On établit ainsi à la fois l'existence et l'unicité de la droite perpendiculaire.
Remarque : L'unicité résulte du fait qu'il n'existe qu'une seule droite passant par deux points distincts C et P. De plus, dans le triangle isocèle ABC, la médiane CP coïncide également avec la bissectrice de l'angle au sommet C. Comme un angle admet une unique bissectrice, cela confirme l'unicité de la droite s.
B] Le point P n'appartient pas à la droite (P ∉ r)
Considérons maintenant une droite r et un point P du plan n'appartenant pas à cette droite.
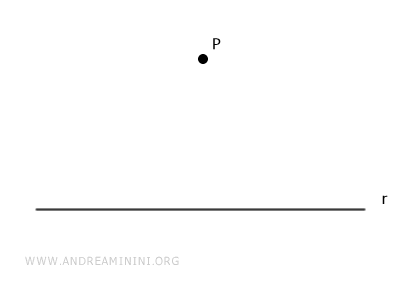
On choisit un point quelconque A sur la droite r et l'on trace le segment AP.
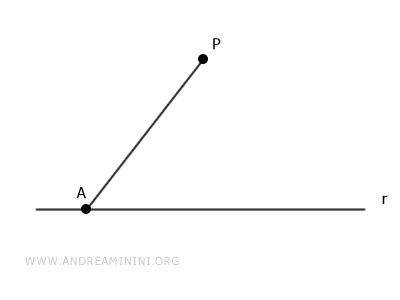
On centre le compas en A et l'on trace un arc de cercle de rayon AP.
Le point d'intersection de cet arc avec la droite r est noté B.
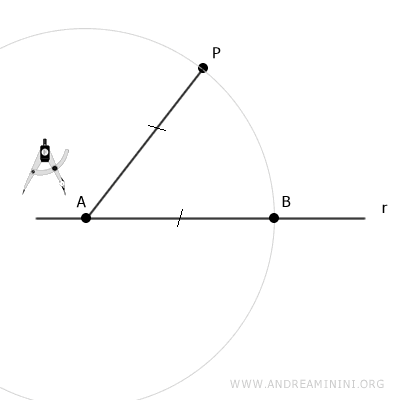
Par construction, les segments AP et AB sont congruents.
$$ \overline{AP} \cong \overline{AB} $$
On centre ensuite le compas en B et l'on trace un second arc de cercle de rayon BP.
Les deux arcs se coupent aux points P et C.
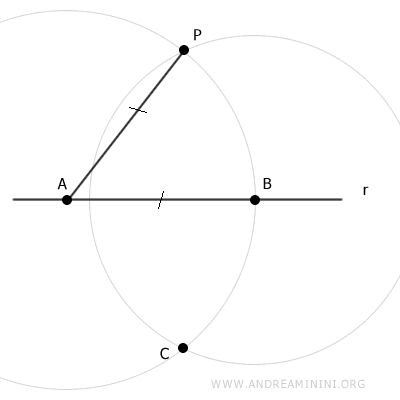
On trace le segment CP reliant les points P et C.
Ce segment coupe la droite r au point D.
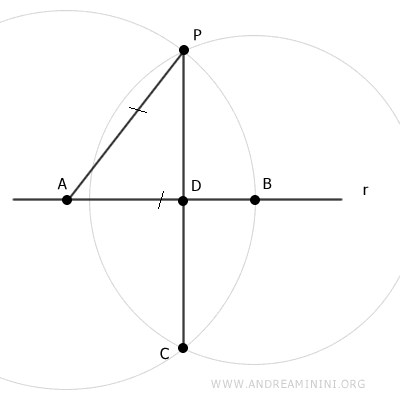
On trace ensuite le segment AC, congruent au segment AP par construction (AC≅AP).
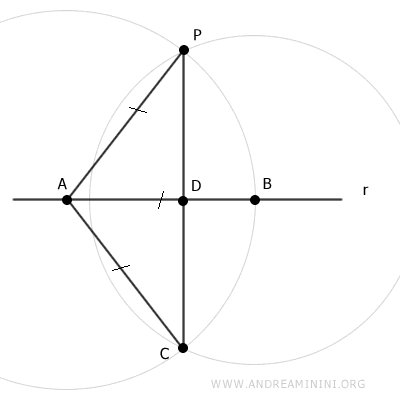
De même, on trace les segments BP et BC, également congruents par construction (BP≅BC).
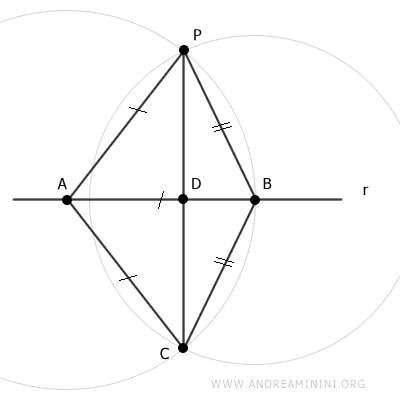
D'après le troisième critère de congruence des triangles (côté-côté-côté), les triangles APB et ACB sont congruents, puisqu'ils partagent le côté AB et possèdent deux autres côtés respectivement congruents : AP≅AC et BP≅BC.
$$ APB \cong ACB $$
Il en résulte que les angles correspondants de ces triangles sont de même mesure.
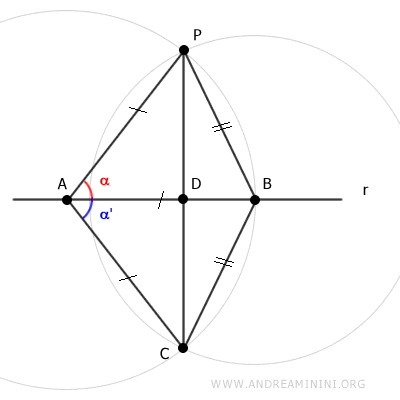
On s'intéresse en particulier à la congruence des angles α et α'.
On en déduit que les triangles APD et ACD sont congruents, puisqu'ils possèdent un angle congruent (α≅α'), un côté congruent (AP≅AC) et le côté commun AD.
$$ APD \cong ACD $$
Il en résulte que les segments PD et CD sont congruents (PD≅CD).
Par conséquent, le point D est le milieu du segment PC.
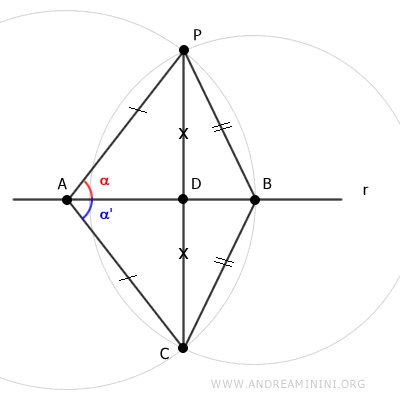
Considérons alors le triangle APC, qui est un triangle isocèle, puisque ses côtés AP et AC sont égaux.
Le segment AD est la médiane de ce triangle, car il relie le sommet A au milieu D du côté opposé PC.
Dans un triangle isocèle, la médiane coïncide avec la hauteur et également avec la bissectrice de l'angle au sommet.
Remarque : Par définition, la hauteur d'un triangle est le segment issu d'un sommet et perpendiculaire au côté opposé ou à son prolongement.
Il s'ensuit que le segment AD est perpendiculaire au segment PC.
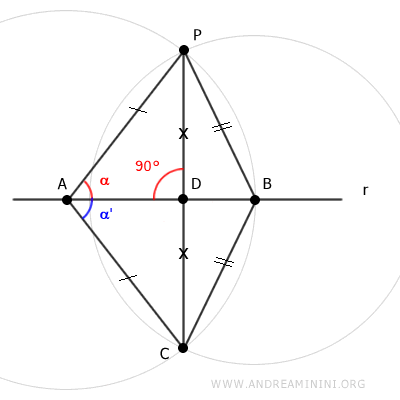
Ainsi, comme il n'existe qu'une seule droite passant par deux points distincts, la droite s passant par les points P et C est perpendiculaire à la droite r passant par les points A et B.
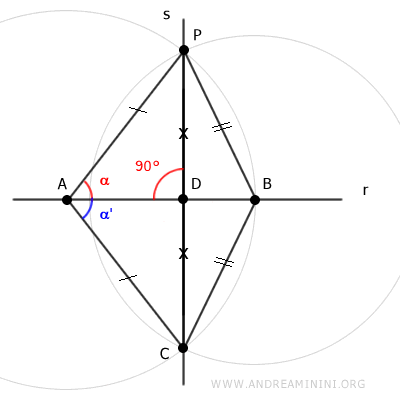
Remarque : Outre le fait qu'il n'existe qu'une seule droite passant par deux points distincts, l'unicité s'explique également par le caractère isocèle du triangle APC. Dans un triangle isocèle, la médiane AD coïncide avec la bissectrice de l'angle au sommet A. On en déduit que la droite r est perpendiculaire à la droite s, et réciproquement.
On a ainsi démontré qu'il existe exactement une droite s perpendiculaire à la droite r et passant par le point C.
$$ r \perp s $$
Vérification : Si l'on choisit un autre point E sur la droite r, distinct du point D, sachant que le segment PD est perpendiculaire à r, les points P, D et E forment un triangle rectangle.
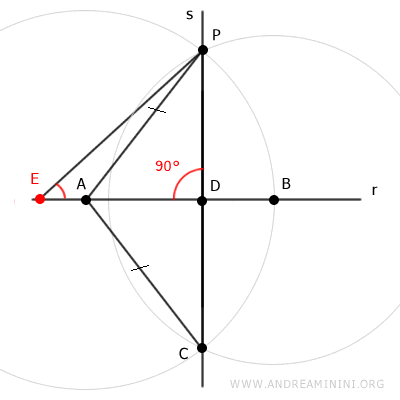
Dans un triangle rectangle, il n'existe qu'un seul angle droit, de 90°. Dans ce cas, cet angle droit est situé au sommet D. Les deux autres angles du triangle PDE sont donc nécessairement aigus, strictement inférieurs à 90°. Il s'ensuit que le segment PE ne peut pas être perpendiculaire à la droite r. Le même raisonnement s'applique à tout autre point E de la droite r distinct de D.
Et ainsi de suite.