Troisième critère de congruence des triangles
Deux triangles sont congruents si leurs trois côtés correspondants sont égaux et disposés dans le même ordre.
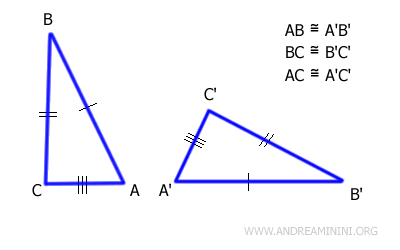
En pratique, cela signifie que deux triangles ont exactement la même forme et la même taille lorsque chacun de leurs côtés correspondants a la même longueur et que ces côtés se succèdent dans le même ordre.
Ce critère est couramment appelé CCC (Côté-Côté-Côté) ou, dans la littérature anglophone, SSS (Side-Side-Side).
Considérons les triangles ABC et A'B'C'.
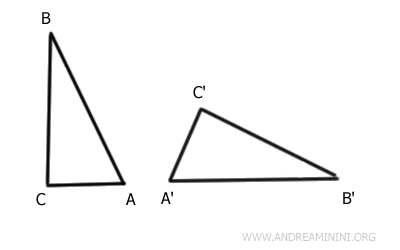
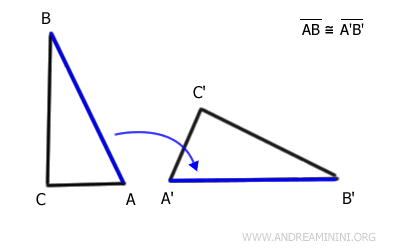
En appliquant une transformation isométrique, par exemple une translation suivie d’une rotation, le côté AB du premier triangle peut être superposé exactement au côté A'B' du second.
Les segments AB et A'B' sont donc congruents.
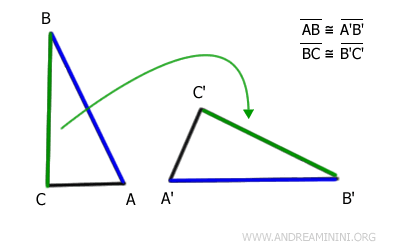
On examine ensuite les côtés adjacents BC et B'C'.
Après une nouvelle transformation isométrique, le côté BC se superpose parfaitement au côté B'C'.
Les segments BC et B'C' sont eux aussi congruents.
Enfin, on considère les côtés AC et A'C'.
À l’aide d’une transformation supplémentaire, le côté AC coïncide exactement avec le côté A'C'.
Les segments AC et A'C' sont donc également congruents.
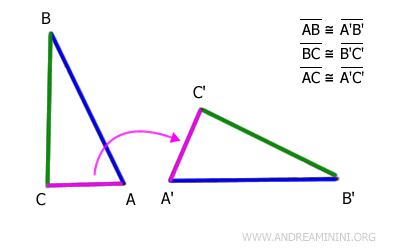
Ainsi, les trois côtés des deux triangles sont congruents et disposés dans le même ordre.
On peut en conclure que les deux triangles sont congruents.
Démonstration
Le critère CCC est un véritable théorème, car il peut être démontré de manière rigoureuse.
Reprenons les triangles ABC et A'B'C' introduits précédemment.
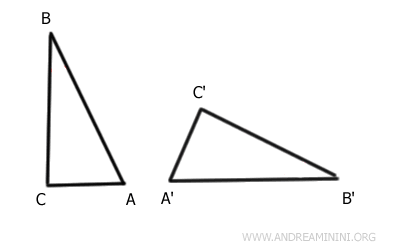
On suppose que :
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
Notre objectif est de montrer que $ ABC \cong A'B'C' $.
On applique une transformation isométrique, composée d’une translation, d’une rotation et, si nécessaire, d’une réflexion, afin de faire coïncider les segments AB et A'B'.
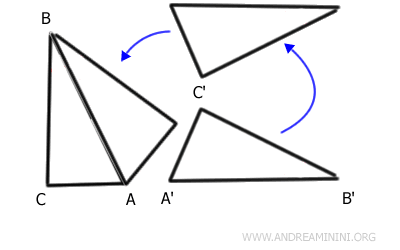
On note C'' l’image du sommet C par cette transformation.
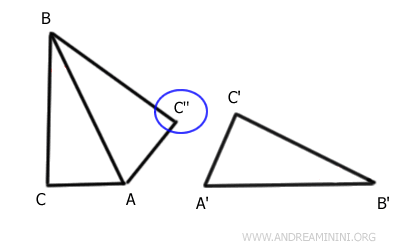
On obtient alors :
$$ AC''B \cong A'B'C' $$
Relions maintenant les points C et C'' par le segment $ \overline{CC''} $.
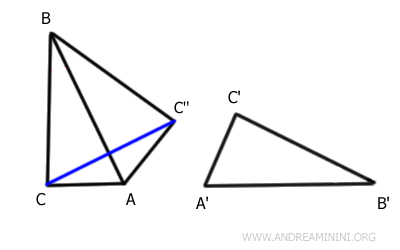
Le triangle AC''C est isocèle, de base $ \overline{CC''} $, puisque $ \overline{AC} \cong \overline{AC''} $.
On en déduit :
$$ \widehat{ACC''} \cong \widehat{AC''C} $$
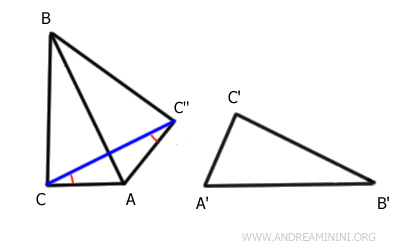
De même, le triangle CBC'' est isocèle, de base $ \overline{CC''} $, car $ \overline{BC} \cong \overline{BC''} $.
On obtient alors :
$$ \widehat{BCC''} \cong \widehat{BC''C} $$
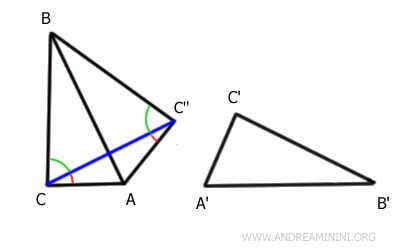
La somme de ces angles est donc également congruente :
$$ \widehat{ACB} \cong \widehat{AC''B} $$
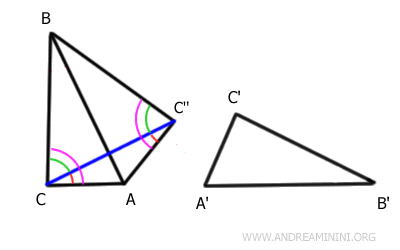
Comme $ \overline{AC} \cong \overline{AC''} $ et $ \overline{BC} \cong \overline{BC''} $, on peut appliquer le premier critère de congruence :
$$ ABC \cong ABC'' $$
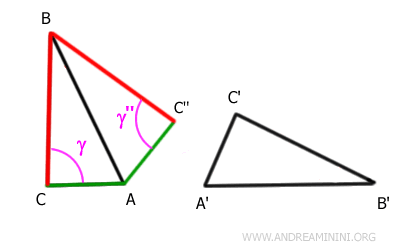
Enfin, comme $ ABC'' \cong A'B'C' $, la transitivité de la congruence permet de conclure :
$$ ABC \cong A'B'C' $$
La démonstration est ainsi achevée.
Démonstration alternative
Considérons à nouveau deux triangles ABC et A'B'C' dont les côtés correspondants sont congruents :
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
On construit un rayon $ A''B $ formant au sommet B un angle égal à $ \beta' $, avec $ \overline{A''B} \cong \overline{A'B'} $.
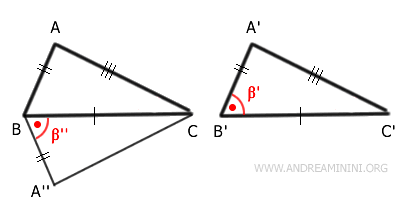
Les triangles $ A''BC $ et $ A'B'C' $ possèdent :
- un côté congruent : $ \overline{BC} \cong \overline{B'C'} $
- un deuxième côté congruent : $ \overline{A''B} \cong \overline{A'B'} $
- l’angle compris congruent : $ \beta' \cong \beta'' $
Le premier critère de congruence s’applique alors :
$$ A''BC \cong A'B'C' $$
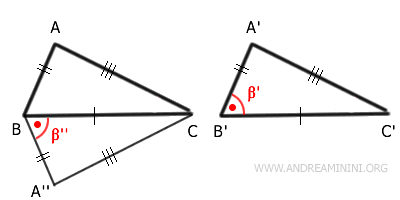
On relie ensuite les points A et A'' par le segment $ \overline{AA''} $. Le triangle $ ABA'' $ est isocèle :
$$ \overline{AB} \cong \overline{A''B} $$
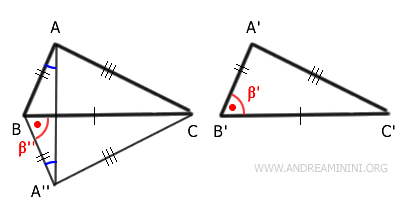
De façon analogue, le triangle $ ACA'' $ est également isocèle :
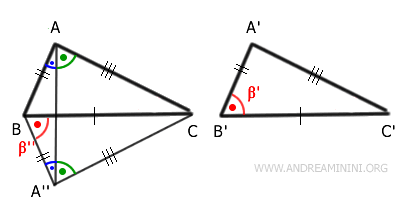
En appliquant une dernière fois le premier critère de congruence, on obtient :
$$ ABC \cong A''BC $$
Comme $ A''BC \cong A'B'C' $, on conclut finalement que :
$$ ABC \cong A'B'C' $$
Démonstration complète.