Droites sécantes

On appelle droites sécantes deux ou plusieurs droites distinctes qui se rencontrent en un point unique.

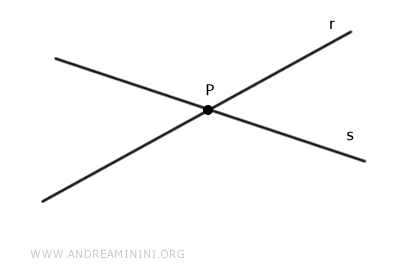
Deux droites sont dites sécantes lorsqu'elles possèdent exactement un seul point commun.

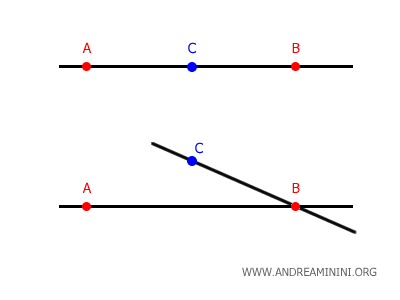
Cette propriété repose sur un principe fondamental de la géométrie euclidienne : par deux points distincts, il ne passe qu'une seule droite.

Lorsque deux droites partagent plus d'un point, on parle alors de droites confondues.

Autrement dit, deux droites ne peuvent être sécantes que si elles admettent un unique point d'intersection.

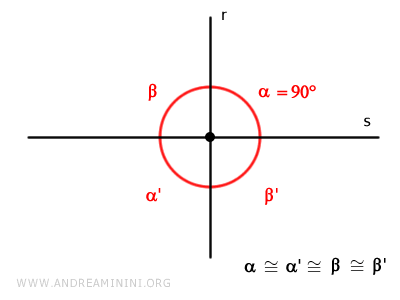
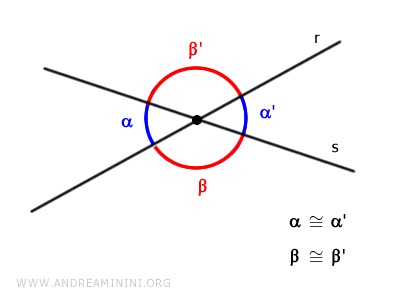
L'intersection de deux droites découpe le plan cartésien en quatre régions et fait apparaître deux paires d'angles opposés par le sommet, égaux deux à deux.

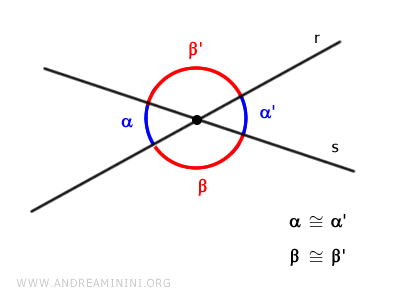
Selon la mesure des angles qu'elles forment, les droites sécantes se répartissent en deux catégories :

• Droites perpendiculaires
  Lorsque les quatre angles opposés par le sommet mesurent 90°, les droites sont dites perpendiculaires.
  
• Droites sécantes non perpendiculaires
  Lorsque deux droites sécantes ne sont pas perpendiculaires, on parle de droites obliques.
  

Déterminer le point d'intersection de deux droites dans le plan

En géométrie analytique, le point d'intersection de deux droites du plan cartésien se calcule en résolvant un système de deux équations linéaires. $$ \begin{cases} ax+by+c=0 \\ \\ a'x+b'y+c'=0 \end{cases} $$ Chaque équation représente une droite du plan.

La résolution de ce système conduit à trois situations possibles :

• Le système admet une solution unique. Le système est alors compatible. La solution fournit deux valeurs, x et y, correspondant aux coordonnées (x;y) du point d'intersection. Les droites se coupent en un point unique. Ce cas apparaît lorsque les coefficients « a » et « b » ne sont pas proportionnels, ce qui traduit des pentes différentes. $$ \frac{a}{a'} \ne \frac{b}{b'} \Longleftrightarrow m \ne m' $$
• Le système n'admet aucune solution. Le système est incompatible. Les droites sont parallèles et ne se coupent pas. Cette situation se produit lorsque les coefficients « a » et « b » sont proportionnels, tandis que le terme constant « c » ne l'est pas. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
• Le système admet une infinité de solutions. Le système est indéterminé. Les droites sont confondues et ont tous leurs points en commun. Cela se produit lorsque les rapports entre les coefficients et les termes constants sont tous égaux. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

L'algèbre permet ainsi de déterminer l'existence d'un point d'intersection et de caractériser la position relative de deux droites : sécantes, parallèles ou confondues.

Exemple

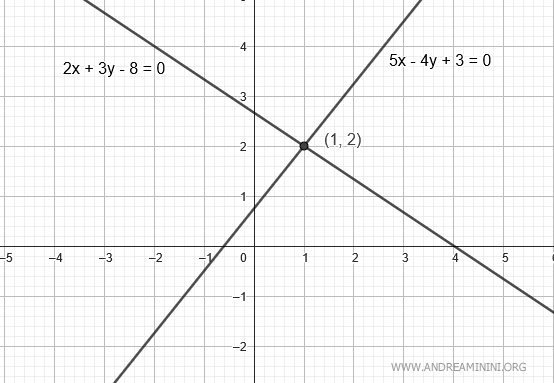
Considérons deux droites définies par les équations implicites suivantes :

$$ r: \ 2x+3y-8=0 $$

$$ r': \ 5x-4y+3=0 $$

Nous cherchons à savoir si ces droites sont sécantes, parallèles ou confondues.

Calculons les rapports entre les coefficients associés aux variables x et y :

$$ \frac{a}{a'} = \frac{2}{5} $$

$$ \frac{b}{b'} = \frac{3}{4} $$

Ces rapports étant différents,

$$ \frac{a}{a'} \ne \frac{b}{b'} $$

les droites sont sécantes.

Remarques

Quelques propriétés utiles concernant les droites sécantes :

• Si deux droites a et b sont sécantes, alors leurs parallèles respectives a' et b' sont également sécantes.
  

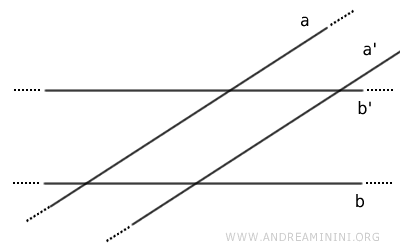
  Démonstration. Raisonnons par l'absurde et supposons le contraire. Si les droites a et b sont sécantes, leurs parallèles respectives a' et b' seraient parallèles entre elles a' // b' $$ a \parallel a' $$ $$ b \parallel b' $$ $$ a' \parallel b' $$ Dans cette hypothèse, par transitivité du parallélisme, les droites a et b seraient elles aussi parallèles $$ a' \parallel b' \ , \ b' \parallel b \Rightarrow a \parallel b $$ ce qui contredit l'hypothèse initiale. L'hypothèse est donc fausse et l'énoncé suivant est vrai : si deux droites a et b sont sécantes, alors leurs parallèles respectives a' et b' sont également sécantes.

Et ainsi de suite