Droites perpendiculaires

On appelle droites perpendiculaires deux droites sécantes qui partagent le plan en quatre angles droits de 90°.

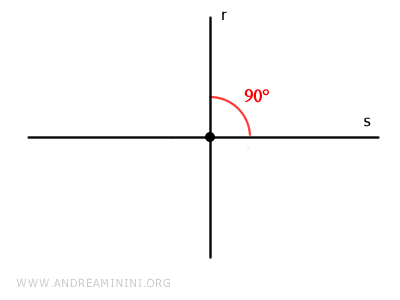
Pour signaler la perpendicularité entre deux droites, on utilise le symbole suivant : $$ r \perp s $$

Considérons deux droites distinctes r et s situées dans un même plan.

Ce sont des droites sécantes, car elles se coupent en un point unique P, appelé le pied de la perpendiculaire.

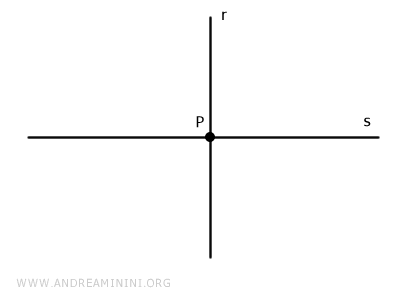
Leur point d'intersection partage le plan cartésien en quatre régions et engendre quatre angles.

Si l'un de ces angles est un angle droit, c'est-à-dire de 90°, alors les trois autres sont automatiquement des angles droits.

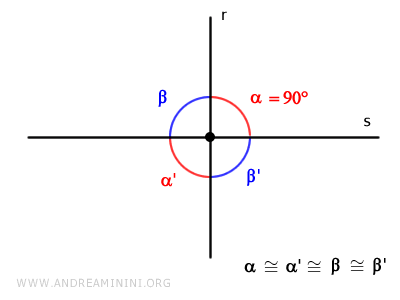
Dans cette situation, on dit que les deux droites sont perpendiculaires.

Explication : Pour deux droites sécantes, les angles opposés par le sommet sont congruents. On a donc α≅α' et β≅β'. $$ \alpha \cong \alpha ' $$ $$ \beta \cong \beta ' $$ Si l'un des angles est droit, par exemple α=90°, alors son angle opposé α' est également droit. $$ \alpha = \alpha ' = 90° $$ La somme de ces deux angles est donc de 180°. $$ \alpha + \alpha' = 90° + 90° = 180° $$ La somme des angles autour d'un point étant égale à 360°, les deux angles restants β et β' doivent eux aussi totaliser 180°. $$ \alpha + \alpha ' + \beta + \beta ' = 360° $$ $$ \beta + \beta ' = 360° - ( \alpha + \alpha' ) = 180° $$ Comme β et β' sont congruents, chacun mesure 90°. $$ \beta = \beta ' = \frac{180°}{2} = 90° $$ Les quatre angles formés sont donc tous droits.

Étant donnée une droite r et un point P situé en dehors de celle-ci, il existe une seule droite passant par P et perpendiculaire à r.

Lorsqu'une droite coupe une autre sans former d'angle droit, on parle alors de droite oblique.

Comment savoir si deux droites sont perpendiculaires ?

En géométrie analytique, deux droites d'équations $ y=mx+q $ et $ y=m'x+q' $ sont perpendiculaires si le produit de leurs coefficients directeurs vaut -1 :

$$ m \cdot m' = -1 $$

Lorsque les équations sont écrites sous forme implicite, $ ax+by+c=0 $ et $ a'x+b'y+c'=0 $, la perpendicularité est caractérisée par la condition suivante :

$$ aa' + bb' = 0 $$

Cette condition reste valable même si l'une des droites est parallèle à un axe du repère.

Ainsi, selon la forme des équations, on peut vérifier la perpendicularité de deux droites de la manière suivante : $$ r \perp s \ \Longleftrightarrow \ m \cdot m' = -1 \ \Longleftrightarrow \ aa'+bb' = 0 $$

Les coefficients directeurs des droites perpendiculaires

Deux droites sont perpendiculaires si, et seulement si, le produit de leurs coefficients directeurs m et m' est égal à -1 : $$ m \cdot m' = -1 $$ ce qui équivaut à $$ m = - \frac{1}{m'} $$

Deux droites $ y=mx+q $ et $ y=m'x+q' $ sont perpendiculaires lorsqu'elles se coupent en formant un angle droit de 90°.

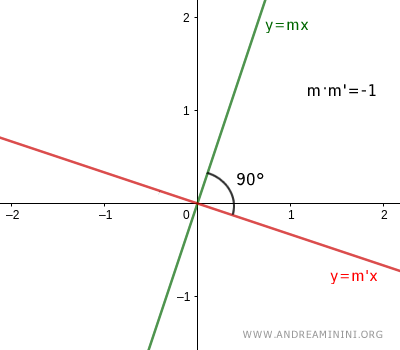
Dans ce cas, le produit de leurs coefficients directeurs est égal à -1 :

$$ m \cdot m' = -1 $$

Autrement dit, leurs coefficients directeurs sont réciproques et de signes opposés :

$$ m = - \frac{1}{m'} $$

Ce résultat n'est valable que si aucune des deux droites n'est parallèle aux axes du repère.

Remarque : Une droite parallèle à l'axe des abscisses a un coefficient directeur nul, et une droite parallèle à l'axe des ordonnées n'a pas de coefficient directeur défini. Dans ces deux cas, la relation précédente ne s'applique pas.

L'énoncé réciproque est également vrai.

Si deux droites ont des coefficients directeurs dont le produit vaut -1, alors elles sont perpendiculaires.

Exemple pratique

Considérons les deux droites suivantes :

$$ r = 2x $$

$$ r' = -\frac{1}{2} x $$

Elles se coupent à l'origine du repère et forment un angle droit de 90°.

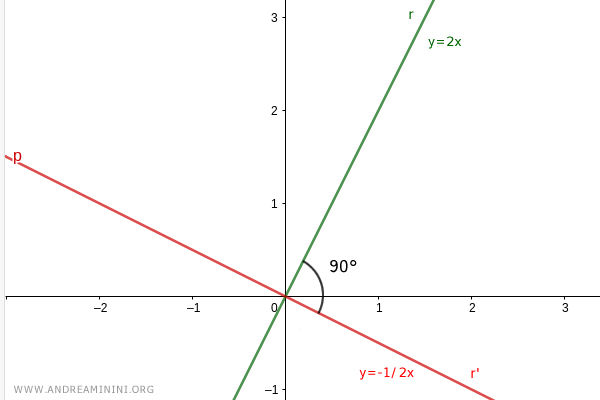
Leurs coefficients directeurs sont bien réciproques et de signes opposés :

$$ m = 2 $$

$$ m' = - \frac{1}{2} $$

Exemple 2

Considérons maintenant :

$$ r = 3x $$

$$ r' = -\frac{1}{3} x $$

Représentons ces droites dans le plan cartésien.

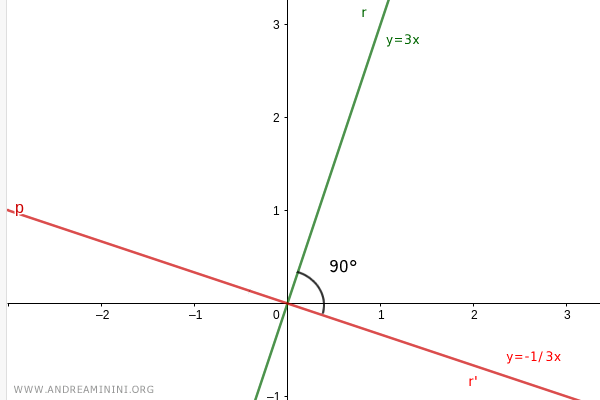
L'angle formé à leur intersection est droit.

Ces deux droites sont donc perpendiculaires.

Démonstration

Considérons deux droites perpendiculaires r et r', non parallèles aux axes du repère :

$$ r: \ y=mx+q $$ $$ r': \ y=m'x+q' $$

Par définition, ces deux droites se coupent en un point et forment quatre angles droits.

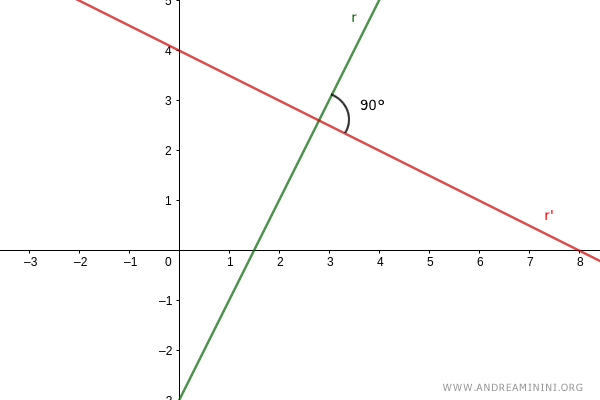
Pour simplifier le raisonnement, considérons les droites parallèles à r et r' passant par l'origine, donc avec q=0 et q'=0.

Elles conservent les mêmes coefficients directeurs m et m'.

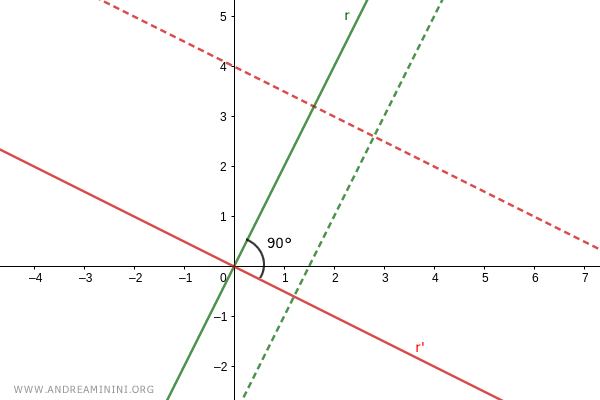
Soit A=(x_A;y_A) un point de la droite r tel que x_A=1.

Sa projection orthogonale sur l'axe des abscisses définit un segment AB.

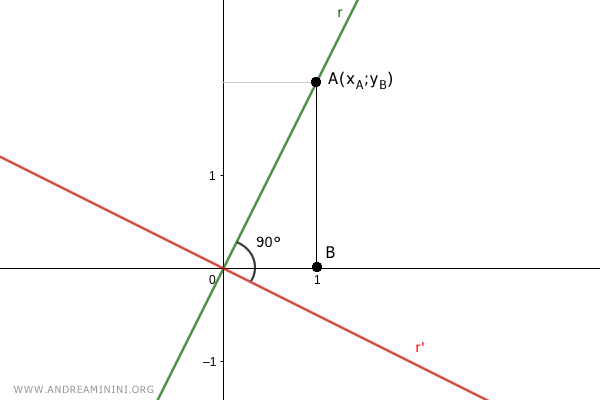
Soit C un point de l'axe des abscisses tel que OC = AB.

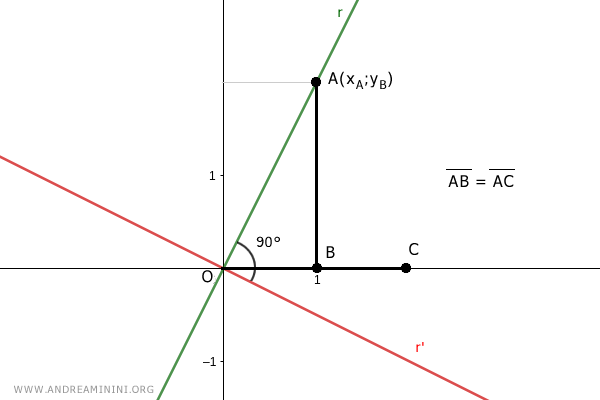
À partir du point C, on trace la perpendiculaire à l'axe des abscisses, qui coupe la droite r' au point D=(x_D;y_D).

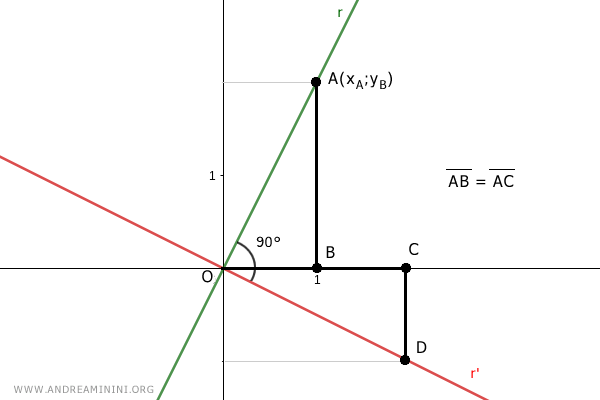
Les triangles rectangles OAB et OCD ont un côté de même longueur, puisque AB = OC par construction.

Ils sont tous deux rectangles et possèdent chacun un angle droit.

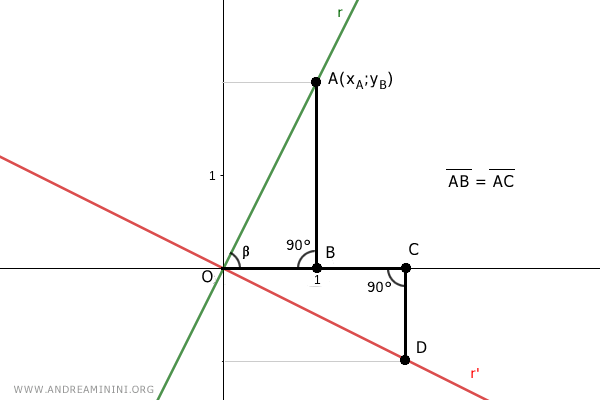
Les angles α et α' sont complémentaires d'un même angle β, ce qui implique qu'ils ont la même mesure.

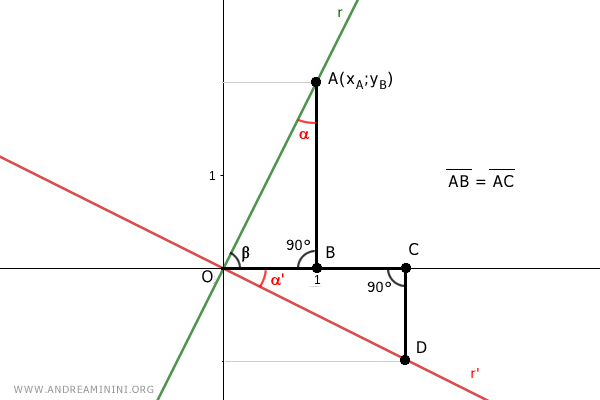
Dans chaque triangle rectangle, la somme des angles vaut 180°. Le troisième angle est donc identique dans les deux triangles.

Les triangles OAB et OCD sont ainsi congruents, puisqu'ils ont des angles égaux et un côté correspondant égal.

On en déduit en particulier que :

$$ \overline{OA} = {CD} $$

Comme OA=1 par construction, on obtient également CD=1.

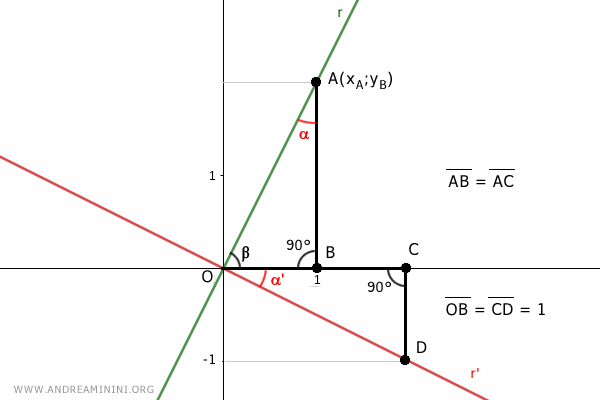
Le point D a donc pour coordonnées D(x_D, -1).

Les coordonnées des points A et D sont :

$$ A=(1;y_A) $$

$$ D=(x_D;-1) $$

Les coefficients directeurs des droites r et r' s'écrivent alors :

$$ m = \frac{y_A}{x_A} = y_A $$

$$ m' = \frac{y_D}{x_D} = \frac{-1}{x_D} $$

Comme AB = OC, on a y_A = x_D.

On retrouve ainsi que les coefficients directeurs sont réciproques et de signes opposés :

$$ m = y_A $$

$$ m' = - \frac{1}{y_A} $$

Démonstration alternative

Considérons deux droites perpendiculaires r et r', qui passent par l'origine du repère O.

On commence par tracer sur l'axe des abscisses positif un segment unitaire tel que OH=1.

On construit ensuite la droite perpendiculaire à l'axe des abscisses passant par le point H, de coordonnées (1;0).

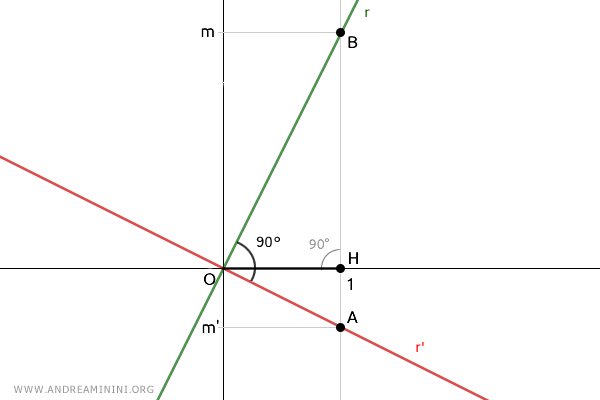
Cette construction géométrique permet d'exprimer simplement les coefficients directeurs des deux droites :

$$ m = \frac{\overline{BH}}{\overline{OH}} $$

$$ m' = \frac{\overline{AH}}{\overline{OH}} $$

Comme OH=1 par construction, ces expressions se simplifient immédiatement :

$$ m = \overline{BH} $$

$$ m' = \overline{AH} $$

Autrement dit, les coefficients directeurs m et m' correspondent directement aux longueurs des segments $ \overline{BH} $ et $ \overline{AH} $.

 

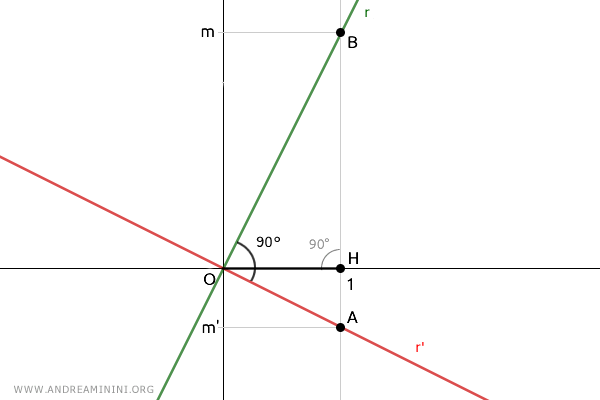
Le triangle OAB est un triangle rectangle. En effet, les segments OA et OB sont portés respectivement par les droites r' et r, qui sont perpendiculaires par hypothèse. L'angle en O est donc un angle droit de 90°.

De plus, le segment OH est la hauteur issue du sommet O du triangle OAB, puisqu'il est perpendiculaire à l'hypoténuse AB.

D'après le deuxième théorème d'Euclide, dans un triangle rectangle, le carré de la hauteur relative à l'hypoténuse est égal au produit des longueurs des deux segments en lesquels cette hauteur partage l'hypoténuse. On obtient donc :

$$ \overline{OH}^2 = \overline{AH} \cdot \overline{BH} $$

Comme OH=1, cette relation devient :

$$ 1 = \overline{AH} \cdot \overline{BH} $$

Or, les longueurs AH et BH sont précisément les valeurs absolues des coefficients directeurs :

$$ AH = |m'| \qquad BH = |m| $$

Il s'ensuit que :

$$ 1 = |m| \cdot |m'| $$

Le produit des valeurs absolues des coefficients directeurs est donc égal à 1.

Comme les droites sont perpendiculaires, leurs coefficients directeurs sont de signes opposés.

Cela apparaît clairement sur le schéma, où m est positif (m>0), car il correspond au demi-axe positif des ordonnées, tandis que m' est négatif (m<0), car il est associé au demi-axe négatif.

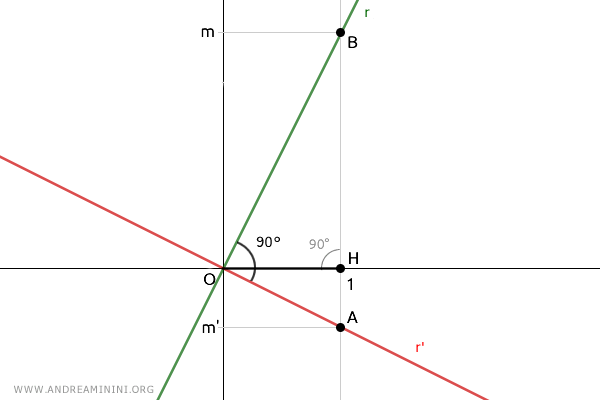
En tenant compte des signes, on obtient finalement la relation :

$$ m \cdot m' = -1 $$

La condition caractéristique de perpendicularité entre deux droites est ainsi établie.

Remarque : Cette démonstration reste valable lorsque les droites perpendiculaires s et s' ne passent pas par l'origine : $$ s: \ y = mx+q \qquad s': \ y = m'x+q' $$ Il suffit de considérer leurs droites parallèles r et r', qui passent par l'origine : $$ r: \ y = mx \qquad r': \ y = m'x $$ La perpendicularité est conservée par parallélisme.

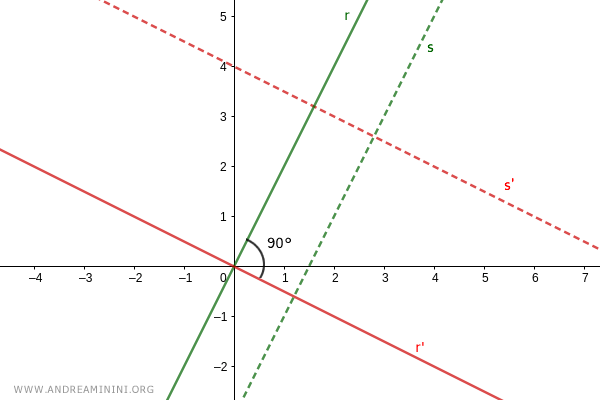
Démonstration réciproque

Partons maintenant de l'hypothèse inverse : le produit des coefficients directeurs de deux droites est égal à -1 :

$$ m \cdot m' = -1 $$

On trace un segment unitaire OH=1 et on construit le triangle OAB :

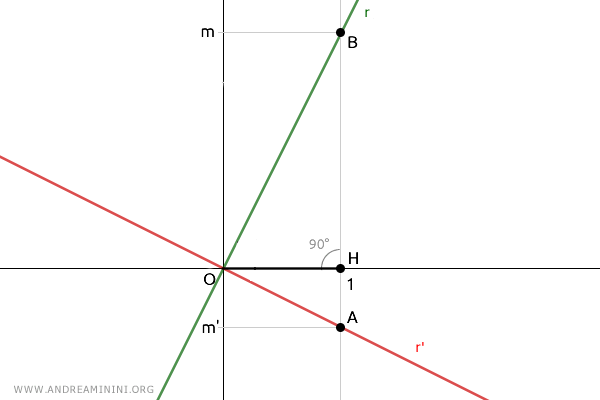
Pour montrer que les droites r et r' sont perpendiculaires, on applique la réciproque du deuxième théorème d'Euclide.

Si, dans un triangle, le carré de la hauteur est égal au produit des longueurs des deux segments en lesquels cette hauteur partage le côté opposé, alors le triangle est rectangle et l'angle au sommet d'où part la hauteur est droit.

$$ \overline{OH}^2 = \overline{AH} \cdot \overline{BH} $$

Dans notre situation, la condition $ m \cdot m' = -1 $ implique :

$$ |m| \cdot |m'| = 1 $$

ce qui revient à écrire :

$$ \overline{AH} \cdot \overline{BH} = 1 $$

Comme OH=1 par construction, on a bien :

$$ \overline{OH}^2 = 1 $$

L'égalité est donc vérifiée.

D'après la réciproque du deuxième théorème d'Euclide, l'angle au sommet O est un angle droit, et le triangle OAB est un triangle rectangle.

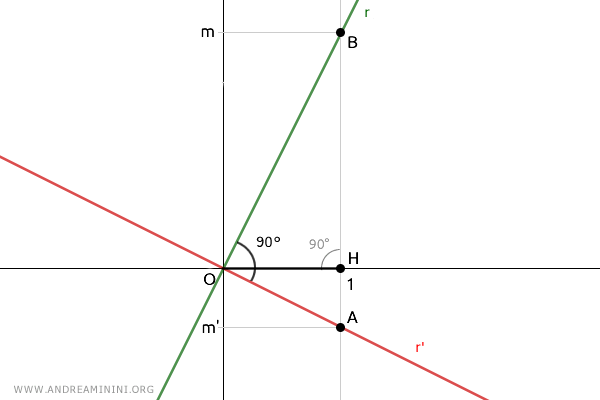
Les segments OA et OB étant perpendiculaires, les droites r' et r sur lesquelles ils reposent sont elles aussi perpendiculaires.

La démonstration est ainsi complète.

La condition de perpendicularité

Deux droites d'équations $ ax+by+c=0 $ et $ a'x+b'y+c'=0 $ sont perpendiculaires si elles vérifient la condition suivante : $$ aa' + bb' = 0 $$

Cette condition est particulièrement utile, car elle permet de vérifier la perpendicularité de deux droites même lorsque l'une d'elles est parallèle à un axe du repère cartésien, situation dans laquelle le calcul du coefficient directeur n'est pas toujours possible.

Exemple

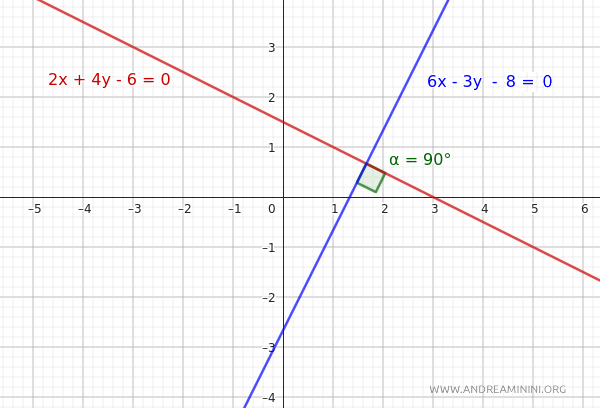
Considérons deux droites données sous forme implicite :

$$ r: 2x+4y-6=0 $$

$$ r': 6x-3y-8=0 $$

Pour savoir si ces deux droites sont perpendiculaires, appliquons la condition de perpendicularité :

$$ aa'+bb'=0 $$

Les coefficients de la première droite sont a=2 et b=4, tandis que ceux de la seconde sont a'=6 et b'=-3. On calcule :

$$ 2 \cdot 6 + 4 \cdot (-3)=0 $$

$$ 12 - 12 = 0 $$

$$ 0 = 0 $$

La condition est vérifiée. Les droites r et r' sont donc perpendiculaires.

Remarque : Pour vérifier rapidement si deux droites sont perpendiculaires sans les représenter graphiquement, on peut écrire leurs équations sous forme implicite l'une sous l'autre, en alignant les coefficients de x et de y, puis calculer mentalement la somme algébrique des produits des coefficients correspondants. Si cette somme est nulle, les droites sont perpendiculaires.

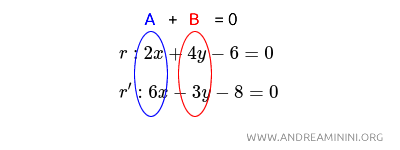
Dans cet exemple, A=2⋅6=12 et B=4⋅(-3)=-12. La somme A+B=12+(-12)=0 confirme immédiatement la perpendicularité.

Démonstration

Considérons deux droites r et s écrites sous forme implicite :

$$ ax+by+c=0 $$

$$ a'x+b'y+c'=0 $$

Leurs coefficients directeurs sont donnés par :

$$ m = - \frac{a}{b} $$

$$ m' = - \frac{a'}{b'} $$

Si deux droites sont perpendiculaires, le produit de leurs coefficients directeurs est égal à -1 :

$$ m \cdot m' = -1 $$

En remplaçant m et m' par leurs expressions, on obtient :

$$ - \frac{a}{b} = \frac{-1}{\left( - \frac{a'}{b'} \right)} $$

$$ - \frac{a}{b} = \frac{b'}{a'} $$

En multipliant en croix, il vient :

$$ -aa' = bb' $$

$$ aa' + bb' = 0 $$

La condition de perpendicularité est ainsi démontrée.

Droite perpendiculaire à un plan

On dit qu'une droite \( r \) est perpendiculaire à un plan \( \alpha \) lorsqu'elle coupe ce plan et qu'elle est perpendiculaire à toutes les droites contenues dans ce plan.

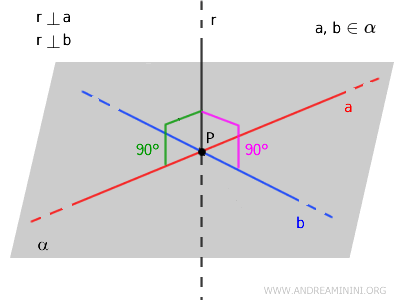
De manière plus concrète, une droite est perpendiculaire à un plan \( \alpha \) si les deux conditions suivantes sont remplies :

• la droite \( r \) coupe le plan \( \alpha \) en un point unique ;
• la droite \( r \) est perpendiculaire à toutes les droites du plan \( \alpha \) passant par ce point.

Cette situation se caractérise aussi par le fait que le vecteur directeur de la droite \( r \) est parallèle au vecteur normal du plan \( \alpha \).

Lorsqu'une droite coupe un plan sans lui être perpendiculaire, on parle de droite oblique.

Observations

Voici quelques propriétés importantes concernant les droites perpendiculaires :

• Théorème de la perpendiculaire
  Étant donné un point P et une droite r dans le plan, il existe une unique droite s passant par P et perpendiculaire à la droite r.
  
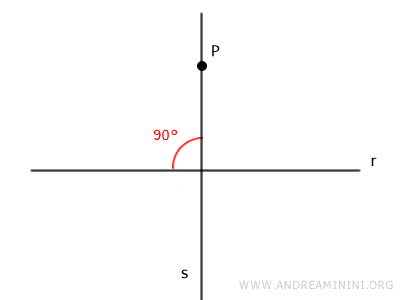
• Deux droites perpendiculaires à une même droite sont parallèles entre elles
  Si deux droites r et s sont toutes deux perpendiculaires à une droite t, alors elles sont parallèles entre elles. Ce résultat découle du théorème des droites parallèles, à partir de l'égalité des angles correspondants.
  
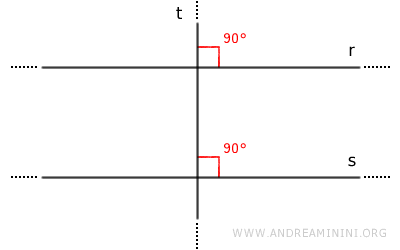
• Une droite perpendiculaire à une droite est perpendiculaire à toutes ses parallèles
  Si deux droites r et s sont parallèles et si une droite t est perpendiculaire à l'une d'elles, alors t est également perpendiculaire à l'autre.
  

  Démonstration : Supposons r//s et une droite t perpendiculaire à s. L'angle formé entre t et s est droit (α=90°). Comme r et s sont parallèles, les angles correspondants α et β formés avec la transversale t sont congruents. L'angle β est donc lui aussi droit, ce qui montre que t est perpendiculaire à r.

• Les perpendiculaires à deux droites sécantes sont elles-mêmes sécantes
  Étant données deux droites sécantes r et s, leurs perpendiculaires respectives p et q se coupent également.
  

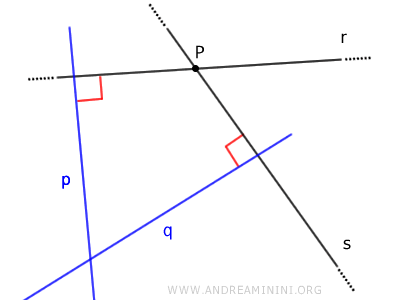
  Démonstration : Raisonnons par l'absurde. Supposons que p et q, perpendiculaires respectivement à r et s, soient parallèles. Dans ce cas, certains angles intérieurs alternes devraient être supplémentaires et totaliser 180°. Or, ces angles proviennent de la subdivision d'angles droits et sont donc aigus. Leur somme est alors strictement inférieure à 180°, ce qui contredit l'hypothèse initiale. Les droites p et q ne peuvent donc pas être parallèles et doivent nécessairement être sécantes.

Ces propriétés constituent une base solide pour l'étude géométrique des droites perpendiculaires, aussi bien dans le plan que dans l'espace.