Projections orthogonales
La projection orthogonale d'un point P sur une droite r est le point d'intersection entre la droite r et la perpendiculaire tracée par P.
Pour fixer les idées, considérons un point P et une droite r.
La projection orthogonale est alors le point P', c'est-à-dire le point où la perpendiculaire issue de P coupe la droite r.
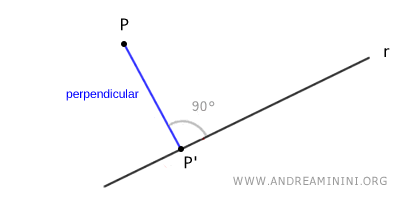
Dans cette situation, la projection orthogonale de P sur la droite r est donc le point P'.
Le segment \( PP' \), qui relie le point à sa projection, représente la distance minimale entre le point P et la droite r.
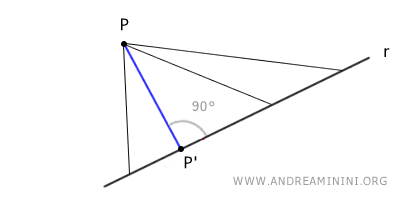
Par un point extérieur à une droite passe une unique perpendiculaire. Autrement dit, il existe une seule droite passant par P et perpendiculaire à r.
Une perpendiculaire est une droite ou un segment qui passe par un point et coupe une autre droite en formant un angle droit (90°). Dans le plan euclidien, elle correspond à la plus courte distance entre un point et une droite.
Démonstration
Pour mettre en évidence l'existence et l'unicité de la perpendiculaire menée d'un point P à une droite r, considérons deux points A et B appartenant à la droite r, situés de part et d'autre du pied P' de la perpendiculaire, tels que \( AP' \cong BP' \).
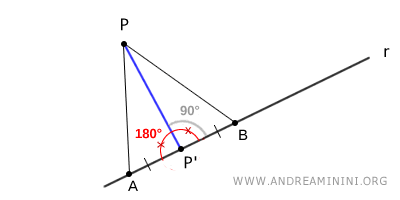
La perpendiculaire coupe la droite r en formant un angle droit et partage l'angle plat \( \angle A\hat{P'}B = 180^\circ \) en deux angles égaux.
Or, un angle plat ne possède qu'une seule bissectrice. Il s'ensuit que la perpendiculaire menée du point P à la droite r est nécessairement unique.
Projection orthogonale d'un segment
La projection orthogonale d'un segment se construit selon le même principe.
Supposons que l'on considère un segment AB et une droite r.
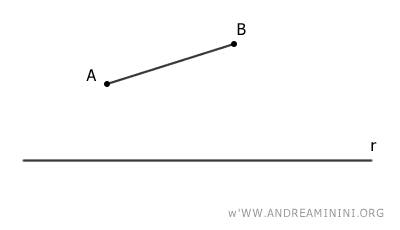
On projette orthogonalement les extrémités A et B sur la droite r, puis on relie les points A' et B' obtenus.
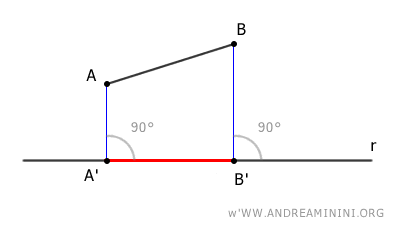
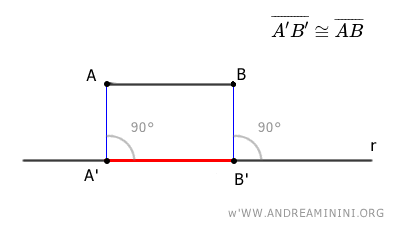
La projection orthogonale du segment AB sur la droite r est ainsi le segment A'B'.
Remarque : La projection orthogonale A'B' d'un segment sur une droite est congruente au segment AB uniquement lorsque le segment est parallèle à la droite.
Dans tous les autres cas, la longueur de la projection orthogonale est toujours inférieure ou égale à celle du segment initial : $$ \overline{A'B'} \le \overline{AB} $$ Dans le cas particulier où le segment est perpendiculaire à la droite, sa projection orthogonale se réduit à un seul point.
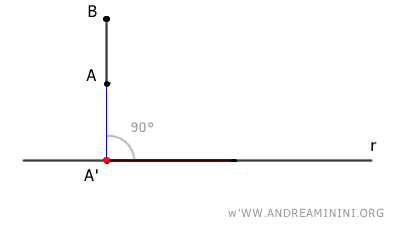
Et l'on procède de la même manière pour des configurations plus complexes.