Théorème des droites perpendiculaires à un même plan

Lorsque deux droites $ r $ et $ s $ sont perpendiculaires à un même plan $ \alpha $, elles sont nécessairement parallèles entre elles. On écrit alors $ r \parallel s $.
deux droites perpendiculaires à un même plan et parallèles entre elles

Démonstration
Remarques complémentaires

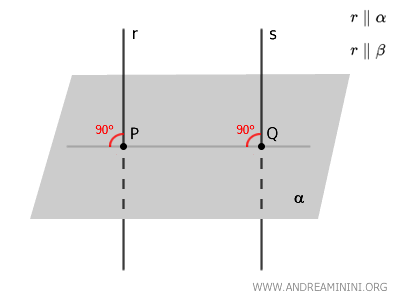
Démonstration

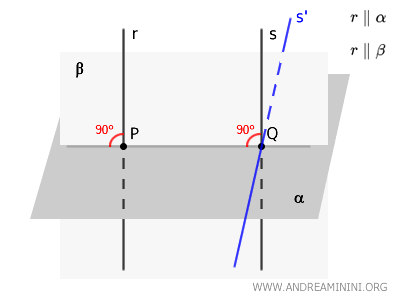
Considérons deux droites $ r $ et $ s $ perpendiculaires au plan $ \alpha $.

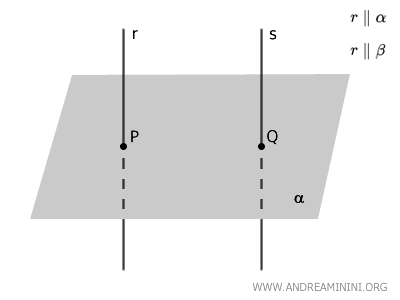
deux droites perpendiculaires à un plan selon l’hypothèse de départ

Les points $ P $ et $ Q $ sont les pieds des perpendiculaires issues respectivement des droites $ r $ et $ s $ sur le plan $ \alpha $.

$$ r \perp \alpha $$

$$ s \perp \alpha $$

Par définition, une droite perpendiculaire à un plan est perpendiculaire à toute droite contenue dans ce plan et passant par le pied de la perpendiculaire. Elle forme donc un angle droit ($90^\circ$) avec chacune de ces droites.

En particulier, les droites $ r $ et $ s $ sont toutes deux perpendiculaires à la droite $ PQ $, qui appartient au plan $ \alpha $ et relie les points $ P $ et $ Q $.

droites perpendiculaires à une même droite du plan

Définissons maintenant le plan $ \beta $ comme le plan déterminé par la droite $ r $ et la droite $ PQ $.

Par construction, les droites $ r $ et $ PQ $ sont contenues dans le plan $ \beta $.

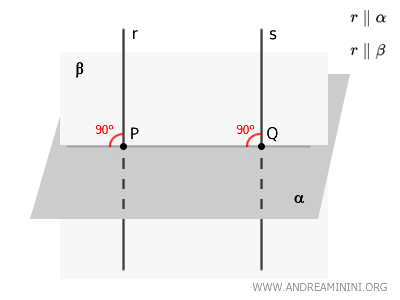
plan beta défini par une droite perpendiculaire au plan alpha et une droite du plan

Supposons à présent, par raisonnement par l’absurde, que les droites $ r $ et $ s $ ne soient pas parallèles.

Deux situations sont alors possibles : soit elles se coupent, soit elles ne sont ni parallèles ni sécantes.

Dans chacun de ces cas, une contradiction apparaît :

Si les droites $ r $ et $ s $ se coupent dans le plan $ \beta $, alors au moins l’une d’elles forme avec la droite $ PQ $ un angle différent de $90^\circ$. Cela contredit le fait qu’une droite perpendiculaire au plan $ \alpha $ est perpendiculaire à toute droite de ce plan passant par son pied, en particulier à $ PQ $.
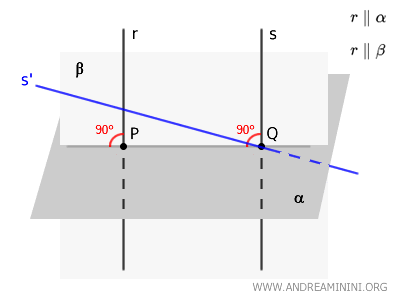
Si les droites $ r $ et $ s $ ne se coupent pas et ne sont pas parallèles, ce sont des droites gauches. Dans ce cas, au moins l’une d’entre elles ne peut être perpendiculaire au plan $ \alpha $, ce qui contredit l’hypothèse initiale $ r \perp \alpha $ et $ s \perp \alpha $.

L’hypothèse selon laquelle les droites $ r $ et $ s $ ne seraient pas parallèles conduit donc nécessairement à une contradiction.

On en conclut que les droites $ r $ et $ s $ sont parallèles.

Remarques complémentaires

Ce théorème mérite d’être complété par quelques observations importantes.

Droites perpendiculaires à une même droite dans l’espace
Dans l’espace tridimensionnel (3D), l’affirmation selon laquelle deux droites perpendiculaires à une même droite seraient parallèles est fausse en général. Cette propriété n’est valable que dans le plan (2D), où les contraintes géométriques sont plus restrictives.

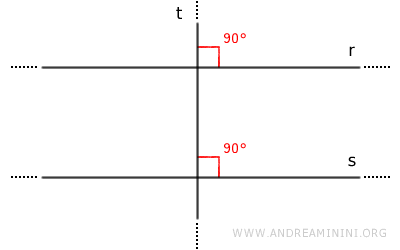
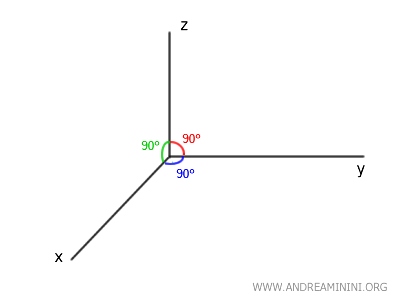
Pourquoi cette propriété est-elle vraie dans le plan mais pas dans l’espace ? Dans un plan bidimensionnel, deux droites perpendiculaires à une même droite ont nécessairement la même direction, ce qui impose leur parallélisme. En revanche, dans l’espace tridimensionnel, une droite donnée admet une infinité de directions perpendiculaires possibles, réparties dans des plans distincts. Deux droites peuvent donc être perpendiculaires à une même droite sans être parallèles.
Exemple : Dans un repère cartésien tridimensionnel, les axes ($x$, $y$, $z$) sont deux à deux perpendiculaires et forment des angles droits ($90^\circ$) entre eux :
- l’axe $x$ est perpendiculaire aux axes $y$ et $z$.
- l’axe $y$ est perpendiculaire aux axes $x$ et $z$.
- l’axe $z$ est perpendiculaire aux axes $x$ et $y$.
Pourtant, aucun de ces axes ($x, y, z$) n’est parallèle à un autre, car chacun appartient à un plan distinct ($xy$, $xz$, $yz$).

Et ainsi de suite.