Théorème du plan des droites perpendiculaires à une droite

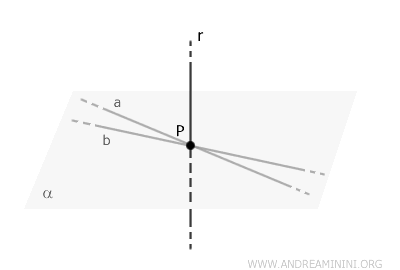
Dans l'espace, toutes les droites perpendiculaires à une droite $ r $ et passant par un point $ P \in r $ sont contenues dans un même plan, noté $ \alpha $.
mise en place du raisonnement par l'absurde

Démonstration

Pour comprendre pourquoi toutes les droites perpendiculaires à $ r $ passant par un même point $ P $ appartiennent à un seul plan, on utilise un raisonnement par l'absurde. L'idée consiste à supposer le contraire et à montrer que cette hypothèse conduit à une impossibilité géométrique.

Considérons donc deux droites distinctes, $ a $ et $ b $, toutes deux perpendiculaires à $ r $ et passant par le point $ P $.

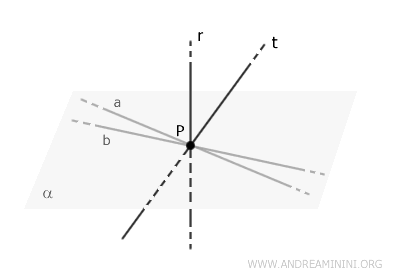
deux droites perpendiculaires passant par P définissent un plan

Ces deux droites déterminent un plan unique, que l'on note $ \alpha $. Par construction, ce plan est perpendiculaire à la droite $ r $ et contient les droites $ a $ et $ b $.

Supposons maintenant qu'il existe une troisième droite $ t $, elle aussi perpendiculaire à $ r $ et passant par le point $ P $, mais qui ne soit pas contenue dans le plan $ \alpha $.

hypothèse d'une droite perpendiculaire hors du plan alpha

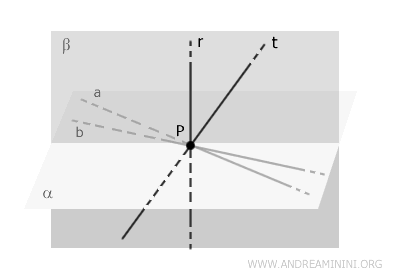
Dans ce cas, les droites $ r $ et $ t $ déterminent un autre plan, noté $ \beta $, distinct du plan $ \alpha $.

Le plan $ \beta $ est donc le plan engendré par la droite $ r $ et la droite $ t $.

plan beta défini par les droites r et t

Les plans $ \alpha $ et $ \beta $ se coupent selon une droite $ s $, qui passe par le point $ P $, puisque ce point appartient aux deux plans.

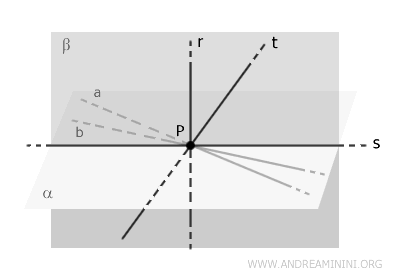
droite d'intersection des plans alpha et beta passant par P

C'est à ce stade que la contradiction apparaît.

La droite $ s $, en tant que droite d'intersection des plans $ \alpha $ et $ \beta $, appartient simultanément aux deux plans.

Or, dans le plan $ \alpha $, les droites $ a $ et $ b $ sont toutes deux perpendiculaires à $ r $. D'après le théorème des trois perpendiculaires, toute droite du plan $ \alpha $ passant par $ P $, et en particulier la droite $ s $, est également perpendiculaire à $ r $.

On obtient alors la situation suivante : dans le plan $ \beta $, il existe deux droites distinctes, $ t $ et $ s $, toutes deux perpendiculaires à $ r $ et passant par le point $ P $. Or, dans un plan, il n'existe qu'une seule droite perpendiculaire à une droite donnée passant par un point donné.

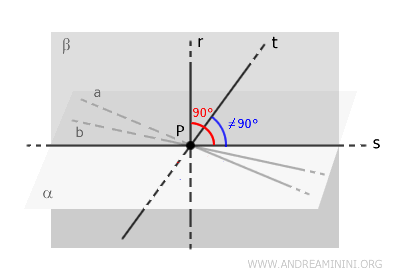
contradiction géométrique finale dans le plan beta

Cette situation étant impossible, l'hypothèse selon laquelle la droite $ t $ n'appartiendrait pas au plan $ \alpha $ doit être rejetée.

On en conclut que toute droite perpendiculaire à $ r $ passant par le point $ P $ est nécessairement contenue dans le plan $ \alpha $.

Ainsi, toutes les droites perpendiculaires à une droite donnée en un point appartiennent à un même plan, ce qui établit le théorème.

Et ainsi de suite.