Théorème des trois perpendiculaires

Si, à partir d'un point $ P $ appartenant à une droite $ r $, on trace deux droites distinctes $ a $ et $ b $, toutes deux perpendiculaires à $ r $, alors la droite $ r $ est perpendiculaire à toute droite $ s $ passant par $ P $ et contenue dans le plan $ \alpha $ déterminé par $ a $ et $ b $.
schéma de principe du théorème des trois perpendiculaires en géométrie de l'espace

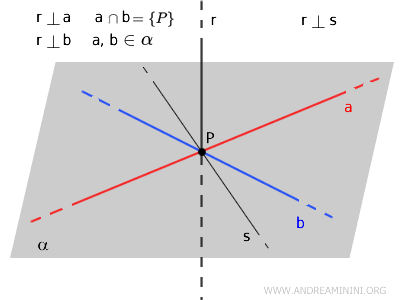
Le théorème des trois perpendiculaires est un résultat central de la géométrie de l'espace. Il joue un rôle clé pour comprendre et démontrer des situations d'orthogonalité entre droites et plans.

Dans la pratique, ce théorème fournit un critère simple et puissant pour établir qu'une droite est perpendiculaire à une autre droite, ou à un plan, en se ramenant à des constructions effectuées dans un plan bien choisi.

Démonstration

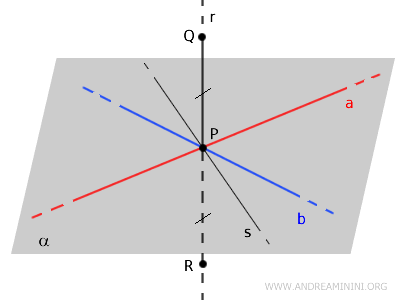
Considérons une droite $ r $ et un point $ P $ situé sur cette droite.

Par le point $ P $, on trace deux droites $ a $ et $ b $, distinctes, toutes deux perpendiculaires à la droite $ r $.

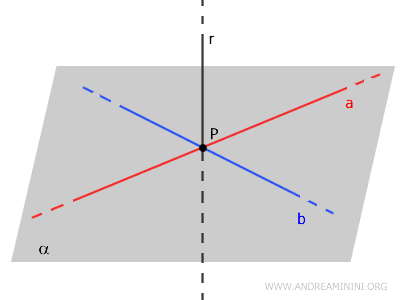
construction de deux droites perpendiculaires à une même droite en un point donné

Ces deux droites déterminent un plan $ \alpha $. Autrement dit, elles sont coplanaires et suffisent à définir entièrement ce plan.

Par construction, les droites $ a $ et $ b $ se coupent en $ P $ et sont toutes deux perpendiculaires à $ r $.

$$ a \cap b = \{ P \} $$

$$ a, b \in \alpha $$

$$ a , b \perp r $$

On en déduit que la droite $ r $ est perpendiculaire au plan $ \alpha $, et que leur intersection se réduit au seul point $ P $.

$$ r \cap \alpha = \{ P \} $$

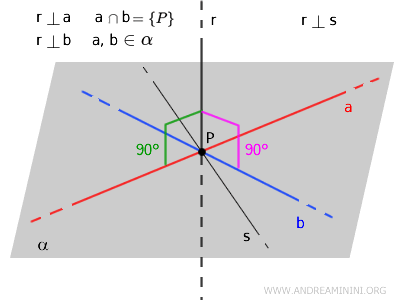
droite perpendiculaire à un plan en un point unique

Choisissons maintenant deux points $ Q $ et $ R $ sur la droite $ r $, situés à la même distance du point $ P $, mais de part et d'autre du plan $ \alpha $.

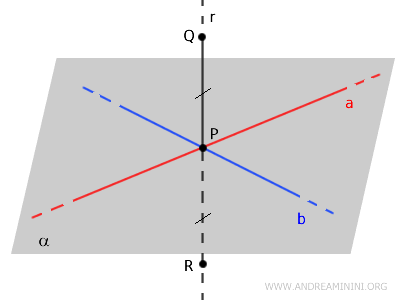
points équidistants de part et d'autre d'un plan sur une droite perpendiculaire

Les points $ Q $ et $ R $ étant équidistants de $ P $, les segments correspondants sont de même longueur :

$$ PQ \cong PR $$

Considérons ensuite une droite $ s $, quelconque, mais entièrement contenue dans le plan $ \alpha $.

droite arbitraire contenue dans le plan alpha

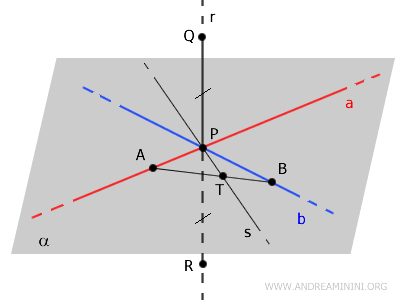
On choisit un point $ A $ sur la droite $ a $ et un point $ B $ sur la droite $ b $. Le segment $ AB $ coupe la droite $ s $ en un point $ T $.

segment reliant deux droites du plan et point d'intersection avec une troisième droite

On construit alors les segments $ AQ, TQ, BQ $ ainsi que $ AR, TR, BR $, ce qui permet de faire apparaître plusieurs triangles utiles à la démonstration.

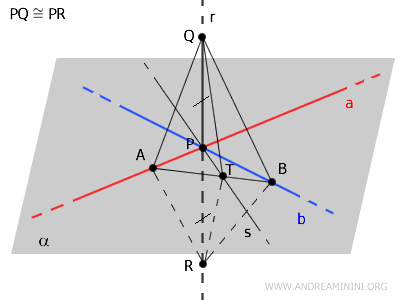
triangles auxiliaires construits dans l'espace pour la démonstration

Dans le triangle $ \triangle AQR $, le segment $ AP $ est à la fois une hauteur et une médiane relatives à la base $ QR $, puisque $ PQ \cong PR $.

Le triangle $ \triangle AQR $ est donc un triangle isocèle, ce qui implique :

$$ AQ \cong AR $$

Un raisonnement strictement analogue s'applique au triangle $ \triangle BQR $. Le segment $ PB $ y est à la fois hauteur et médiane, d'où :

$$ BQ \cong BR $$

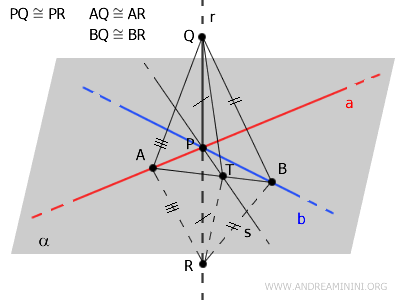
mise en évidence de triangles isocèles dans la construction

Intéressons-nous maintenant aux triangles $ \triangle ABQ $ et $ \triangle ABR $.

D'après le troisième critère de congruence des triangles, ces deux triangles sont congruents. Ils ont en effet le côté $ AB $ commun, ainsi que deux paires de côtés égaux : $ AQ \cong AR $ et $ BQ \cong BR $.

$$ ABQ \cong ABR $$

La congruence implique l'égalité des angles correspondants, en particulier :

$$ \angle ABQ = \angle ABR $$

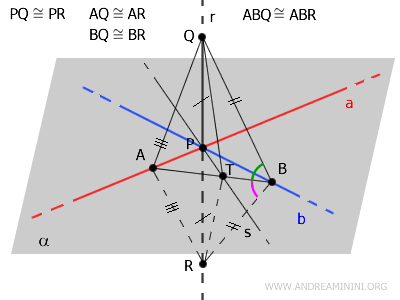
égalité des angles correspondants dans des triangles congruents

Considérons enfin les triangles $ \triangle TBQ $ et $ \triangle TBR $. Le côté $ TB $ est commun, les segments $ BQ $ et $ BR $ sont égaux, et les angles compris sont identiques.

Le premier critère de congruence des triangles permet alors d'affirmer :

$$ TBQ \cong TBR $$

On en déduit immédiatement l'égalité des segments correspondants :

$$ TQ \cong TR $$

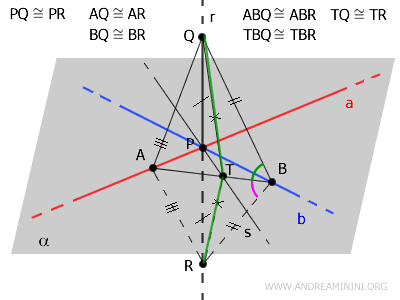
triangle isocèle obtenu à partir des congruences précédentes

Le triangle $ \triangle TQR $ est donc isocèle. Le segment $ PT $ y joue à la fois le rôle de médiane et de hauteur.

Il s'ensuit que $ PT $ est perpendiculaire à la base $ QR $, formant un angle droit :

$$ PT \perp QR $$

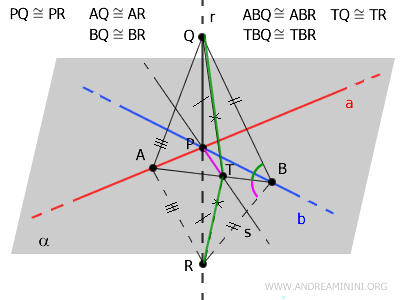
perpendicularité finale entre les droites considérées

Or, le segment $ QR $ appartient à la droite $ r $, tandis que le segment $ PT $ appartient à la droite $ s $.

On conclut donc que les droites $ r $ et $ s $ sont perpendiculaires :

$$ r \perp s $$

Ce raisonnement reste valable pour toute droite $ s $ contenue dans le plan $ \alpha $.

vue d'ensemble illustrant le théorème des trois perpendiculaires

Le théorème des trois perpendiculaires est ainsi rigoureusement établi.

Et ainsi de suite.