Existence et unicité de la droite perpendiculaire à un plan

Étant donné un plan \( \alpha \) et un point \( P \), il existe une et une seule droite \( r \) passant par \( P \) et perpendiculaire au plan \( \alpha \).

Dans l’espace euclidien, tout plan possède une direction perpendiculaire bien définie. Cette direction est décrite par un vecteur normal, qui caractérise l’orientation du plan.

La droite \( r \) passe par le point \( P \) et est orientée suivant la direction d’un vecteur normal au plan \( \alpha \). C’est cette propriété qui la rend perpendiculaire au plan.

Remarque : la direction normale d’un plan est unique, à un facteur scalaire non nul près. Cette unicité implique qu’il ne peut exister qu’une seule droite passant par \( P \) et perpendiculaire au plan \( \alpha \).

Démonstration

Considérons le plan \( \alpha \) et un point arbitraire \( P \) appartenant à ce plan.

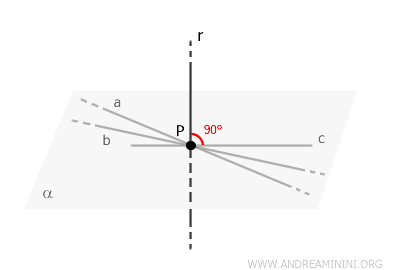
Un plan contient une infinité de points et, par conséquent, une infinité de droites qui lui sont contenues, notées par exemple \( a \), \( b \), \( c \), et ainsi de suite.

Par définition, une droite est perpendiculaire au plan \( \alpha \) si elle forme un angle droit avec toute droite passant par \( P \) et contenue dans le plan \( \alpha \).

Il est donc toujours possible, à partir du point \( P \), de déterminer une droite \( r \) issue de \( P \), perpendiculaire au plan, et formant un angle droit avec chacune des droites du plan \( \alpha \).

Il reste à montrer que cette droite perpendiculaire \( r \) est unique, c’est-à-dire qu’il n’existe aucune autre droite distincte possédant la même propriété.

Supposons, par un raisonnement par l’absurde, qu’il existe deux droites distinctes \( r \) et \( r' \), toutes deux perpendiculaires au plan \( \alpha \) et passant par le point \( P \).

Dans ce cas, au moins l’une des deux droites ne serait pas perpendiculaire à l’une des droites contenues dans le plan \( \alpha \). En effet, si \( r \) et \( r' \) étaient toutes deux perpendiculaires à l’ensemble de ces droites, elles auraient nécessairement la même direction normale et coïncideraient, ce qui contredirait l’hypothèse selon laquelle elles sont distinctes.

Cette contradiction montre qu’il est impossible que deux droites distinctes vérifient simultanément la propriété d’être perpendiculaires au plan \( \alpha \) en passant par \( P \).

On en conclut qu’il existe une unique droite passant par \( P \) et perpendiculaire au plan \( \alpha \).

La proposition est ainsi démontrée.