Théorème des trois droites perpendiculaires

Le théorème des trois droites perpendiculaires est un résultat fondamental de la géométrie de l'espace. Il établit un lien simple et puissant entre la perpendicularité d'une droite à un plan et la perpendicularité de droites contenues dans ce plan.

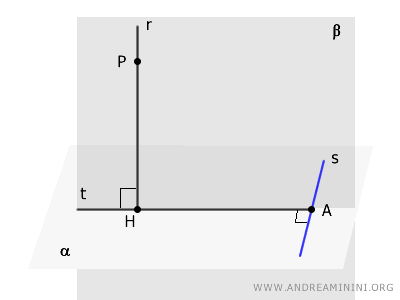
Plus précisément, si, à partir du point $ H $ où une droite $ r $ est perpendiculaire à un plan $ \alpha $, on trace une droite $ t $ perpendiculaire à une droite $ s $ appartenant à ce plan, alors la droite $ s $ est perpendiculaire au plan $ \beta $, déterminé par les droites $ r $ et $ t $.
schéma illustrant le théorème des trois droites perpendiculaires

Démonstration

Considérons un plan $ \alpha $ et une droite $ r $ perpendiculaire à ce plan ($ r \perp \alpha $). Le point $ H $ désigne le pied de cette perpendiculaire. Dans le plan $ \alpha $, on choisit une droite $ s $.

droite perpendiculaire à un plan et droite appartenant au plan

On construit ensuite une droite $ t $, perpendiculaire à $ s $, passant par le point $ H $. Cette droite coupe $ s $ en un point que l'on note $ A $.

construction de la droite t perpendiculaire à s et passant par H

On choisit alors un point quelconque $ P $ sur la droite $ r $, puis on relie ce point au point $ A $ par le segment $ PA $.

choix d'un point P sur la droite r et tracé du segment PA

Sur la droite $ s $, on prend deux points $ B $ et $ C $, placés à la même distance du point $ A $, mais situés de part et d'autre de celui-ci.

On a alors deux segments de même longueur : $ AB \cong AC $.

points B et C équidistants du point A sur la droite s

On relie ensuite les points $ B $ et $ C $ au point $ H $.

Comme le point $ H $ appartient à la médiatrice du segment $ BC $, le triangle $ BCH $ est isocèle. Il en résulte que les segments $ BH $ et $ CH $ ont la même longueur : $ BH \cong CH $.

triangle isocèle BCH formé avec le pied de la perpendiculaire

On relie ensuite les points $ B $ et $ C $ au point $ P $, situé sur la droite $ r $.

Les triangles $ BPH $ et $ CPH $ sont alors congruents. En effet, ils ont le côté $ HP $ en commun, possèdent des côtés correspondants égaux $ BH \cong CH $ et contiennent chacun un angle droit de 90°. On en déduit que les segments $ BP $ et $ CP $ sont égaux : $ BP \cong CP $.

congruence des triangles BPH et CPH

Le triangle $ BCP $ est donc isocèle, puisqu'il présente deux côtés de même longueur.

Par conséquent, le segment $ AP $ est à la fois la médiane, la médiatrice et la hauteur de ce triangle. Il est donc perpendiculaire à la base $ BC $ du triangle $ BCP $, c'est-à-dire à la droite $ s $ :

$$ AP \perp s $$

Enfin, la droite $ s $ étant perpendiculaire à la fois à $ AH $ et à $ AP $, elle est perpendiculaire au plan $ \beta $, défini par les segments $ AH $ et $ AP $. Ce plan est précisément celui engendré par les droites $ r $ et $ t $.

conclusion géométrique du théorème des trois droites perpendiculaires

La démonstration est ainsi complète et met en évidence le rôle central des symétries et des triangles isocèles dans la géométrie de l'espace.