Théorème de Pythagore généralisé
Dans tout triangle rectangle, si l’on construit trois polygones semblables sur ses côtés, l’aire du polygone élevé sur l’hypoténuse est égale à la somme des aires des polygones construits sur les deux autres côtés.
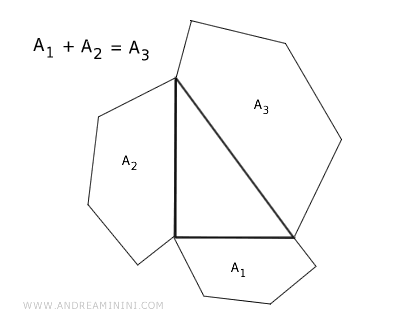
Autrement dit, l’aire du polygone tracé sur l’hypoténuse correspond exactement à la somme des aires des polygones situés sur les catètes.
Ce résultat généralise l’idée fondamentale du théorème de Pythagore : la relation entre les côtés d’un triangle rectangle ne se limite pas aux carrés, mais s’étend à toute figure géométrique semblable construite sur ces côtés.
Remarque : peu importe que l’on choisisse des triangles, des cercles, des polygones réguliers ou toute autre figure semblable ; la somme des aires des figures dressées sur les catètes sera toujours égale à celle du polygone correspondant sur l’hypoténuse.
Exemple illustratif
Considérons un triangle rectangle ABC sur les côtés duquel on construit trois pentagones réguliers.
Les catètes AB et AC mesurent respectivement 4 et 3 unités, tandis que l’hypoténuse BC a une longueur de 5 unités.
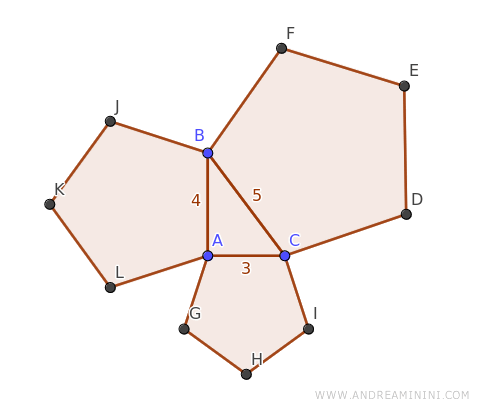
Comme ces pentagones possèdent le même nombre de côtés et la même forme, ils sont bien semblables.
Remarque : il n’est pas nécessaire que les polygones soient réguliers ; il suffit qu’ils soient semblables. Ici, l’on a retenu des pentagones réguliers pour simplifier les calculs, car deux polygones réguliers ayant le même nombre de côtés sont toujours semblables.
Voyons comment calculer l’aire de chaque pentagone.
L’aire d’un polygone régulier se détermine en multipliant son demi-périmètre (p) par l’apothème (a) :
$$ A = p \cdot a $$
Dans le cas du pentagone, l’apothème (a) est égal à la longueur du côté (l) multipliée par une constante (f), qui vaut environ 0,688 pour les pentagones.
$$ A = p \cdot ( l \cdot f ) $$
$$ A = p \cdot ( l \cdot 0.688 ) $$
On obtient ainsi :
- Aire du pentagone sur le côté AB (longueur 3) : $$ A_1 = \frac{3 \cdot 5}{2} \cdot ( 3 \cdot 0.688 ) = 15.48 $$ unités carrées.
- Aire du pentagone sur le côté AC (longueur 4) : $$ A_2 = \frac{4 \cdot 5}{2} \cdot ( 4 \cdot 0.688 ) = 27.52 $$ unités carrées.
- Aire du pentagone sur l’hypoténuse BC (longueur 5) : $$ A_3 = \frac{5 \cdot 5}{2} \cdot ( 5 \cdot 0.688 ) = 43 $$ unités carrées.
Une vérification à l’aide de Geogebra confirme ces résultats :
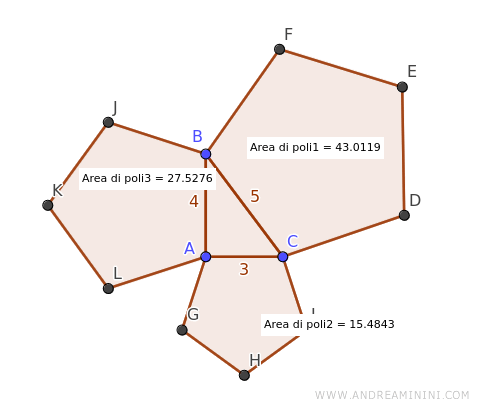
Comme attendu, la somme des aires des polygones sur les catètes est égale à l’aire du polygone sur l’hypoténuse :
$$ A_1 + A_2 = A_3 $$
$$ 15.48 + 27.52 = 43 $$
$$ 43 = 43 $$
L’égalité est parfaitement vérifiée.
Démonstration
Reprenons le triangle rectangle avec trois polygones semblables construits sur ses côtés.

D’après le théorème des aires de polygones semblables, l’aire de ces figures est proportionnelle au carré du côté qui leur sert de base :
$$ \frac{A_3}{A_2} = \left( \frac{c}{b} \right)^2 $$
Donc :
$$ A_3 = A_2 \cdot \left( \frac{c}{b} \right)^2 $$
Or, d’après le théorème de Pythagore :
$$ c^2 = a^2 + b^2 $$
Si l’on pose $$ a = k \cdot b $$, alors :
$$ c^2 = (k b)^2 + b^2 = b^2 (k^2 + 1) $$
Par conséquent :
$$ A_3 = A_2 \cdot \frac{b^2 (k^2 + 1)}{b^2} $$
$$ A_3 = A_2 (k^2 + 1) $$
D’autre part :
$$ k^2 = \frac{A_1}{A_2} $$
soit :
$$ A_1 = k^2 \cdot A_2 $$
Il vient :
$$ A_1 + A_2 = (k^2 \cdot A_2) + A_2 = A_2 (k^2 + 1) $$
Donc :
$$ A_1 + A_2 = A_3 $$
On a ainsi montré que la somme des aires des polygones semblables construits sur les catètes est égale à l’aire du polygone correspondant sur l’hypoténuse.
Autre démonstration
Considérons de nouveau le triangle rectangle ABC avec ses trois polygones semblables :

Le théorème des polygones semblables affirme que :
$$ \frac{A_1}{A_2} = \frac{a^2}{b^2} $$
et
$$ \frac{A_3}{A_2} = \frac{c^2}{b^2} $$
En appliquant la propriété de composition des rapports :
$$ \frac{A_1 + A_2}{A_2} = \frac{a^2 + b^2}{b^2} $$
Or, d’après le théorème de Pythagore :
$$ a^2 + b^2 = c^2 $$
Donc :
$$ \frac{A_1 + A_2}{A_2} = \frac{c^2}{b^2} $$
$$ \frac{A_1 + A_2}{A_2} = \frac{A_3}{A_2} $$
D’où l’on déduit :
$$ A_1 + A_2 = A_3 $$
On a donc confirmé que la somme des aires des polygones semblables érigés sur les catètes d’un triangle rectangle est égale à l’aire du polygone semblable construit sur l’hypoténuse.