Lien entre le produit scalaire et la longueur d’un vecteur

Le produit scalaire d’un vecteur par lui-même est égal au carré de sa norme : $$ \vec{v} \cdot \vec{v} = | \vec{v} |^2 $$

Cette propriété est particulièrement précieuse, car elle permet de déterminer la longueur (ou norme) d’un vecteur de façon directe et élégante.

Il suffit en effet de prendre la racine carrée du produit scalaire du vecteur par lui-même :

$$ | \vec{v} | = \sqrt{ \vec{v} \cdot \vec{v} } $$

Un exemple concret

Considérons le vecteur suivant :

$$ \vec{v} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Sa représentation graphique est la suivante :

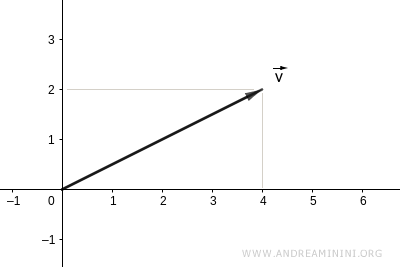
Pour calculer sa norme, commençons par évaluer son produit scalaire avec lui-même :

$$ \vec{v} \cdot \vec{v} = 2 \cdot 2 + 4 \cdot 4 = 2^2 + 4^2 = 4
+ 16 = 20 $$

Comme le produit scalaire d’un vecteur avec lui-même donne le carré de sa norme :

$$ | \vec{v} |^2 = \vec{v} \cdot \vec{v} = 20 $$

On en déduit la norme en prenant la racine carrée du résultat :

$$ | \vec{v} | = \sqrt{ 20 } $$

La longueur du vecteur est donc :

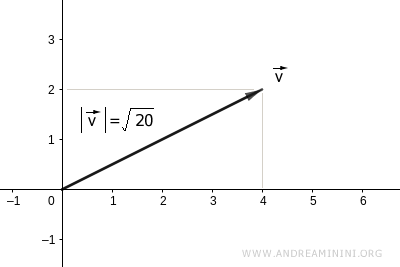
Démonstration

Considérons un vecteur de coordonnées (x, y) :

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $$

Pour simplifier, nous nous plaçons dans le plan, mais le raisonnement s’étend sans difficulté à des espaces de dimension quelconque.

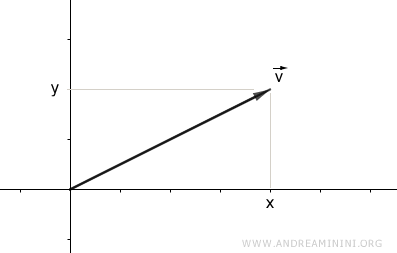
La projection des coordonnées du vecteur (x, y) sur les axes cartésiens forme un triangle rectangle ABC.

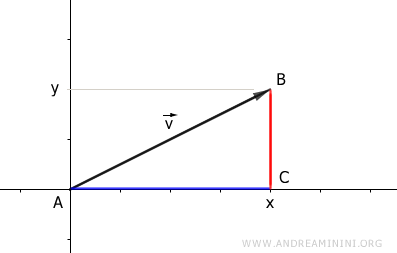
Dans ce triangle, les côtés adjacents correspondent aux projections sur les axes, tandis que la longueur du vecteur (sa norme) correspond à l’hypoténuse.

Le produit scalaire du vecteur par lui-même s’exprime alors comme la somme des carrés des deux côtés adjacents :

$$ \vec{v} \cdot \vec{v} = x \cdot x + y \cdot y = x^2 + y^2 $$

D’après le théorème de Pythagore, la somme des carrés des côtés est égale au carré de l’hypoténuse :

$$ \overline{AB}^2 = \overline{BC}^2 + \overline{AC}^2 $$

Dans ce cadre, AC = x, BC = y et AB représente la norme du vecteur |v| :

$$ | \vec{v} |^2 = x^2 + y^2 $$

On obtient donc que le produit scalaire d’un vecteur par lui-même est exactement le carré de sa norme :

$$ \vec{v} \cdot \vec{v} = x^2 + y^2 = | \vec{v} |^2 $$

Il s’ensuit que la norme d’un vecteur est donnée par la racine carrée de ce produit :

$$ | \vec{v} | = \sqrt{\vec{v} \cdot \vec{v}} $$

Remarque : La norme d’un vecteur est parfois appelée « magnitude ». Ces deux termes désignent la même grandeur scalaire, correspondant à la longueur du vecteur : $$ || \vec{v} || = \sqrt{\vec{v} \cdot \vec{v}} $$

Et ainsi de suite.