Moment d’un vecteur
Qu’est-ce que le moment d’un vecteur ?
Le moment d’un vecteur v, appliqué en un point P par rapport à un point O (appelé pôle), se définit comme le produit vectoriel entre le vecteur de position OP et le vecteur v lui-même : $$ \vec{M} = \vec{OP} × \vec{v} $$ La norme du moment s’exprime ainsi : $$ | \vec{M} | = | \vec{OP} | \cdot | \vec{v} | \cdot \sin θ $$
Ici, θ désigne l’angle formé entre les vecteurs v et OP.
Le moment d’un vecteur est donc, par nature, une grandeur vectorielle.
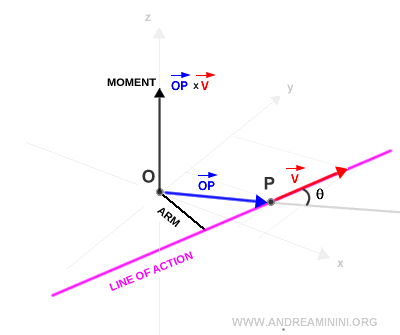
Ce vecteur est perpendiculaire au plan défini par v et par le vecteur de position OP, puisqu’il résulte d’un produit vectoriel.
Remarque. La direction du vecteur v est appelée sa ligne d’action. La distance la plus courte entre cette ligne d’action et le pôle O est appelée le bras de levier du vecteur v par rapport à O.
Propriétés du moment d’un vecteur
On peut résumer les propriétés essentielles du moment d’un vecteur de la manière suivante :
- La norme du moment est nulle lorsque les vecteurs v et OP sont colinéaires. Autrement dit, le moment s’annule si les vecteurs sont parallèles ou confondus. En revanche, il est non nul dès qu’ils forment un angle entre eux.
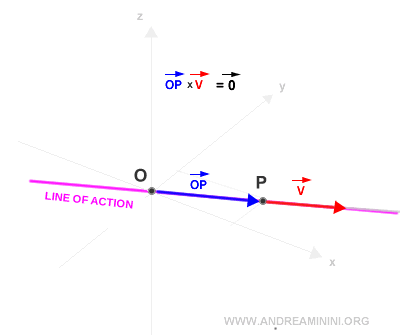
Remarque. Dans ce cas, le bras de levier est nul puisque la ligne d’action passe par le pôle O. Le vecteur moment est donc nul.
- Le déplacement du vecteur v le long de sa ligne d’action ne modifie pas la norme de son moment. Autrement dit, le moment est invariant par translation du vecteur sur sa ligne d’action.
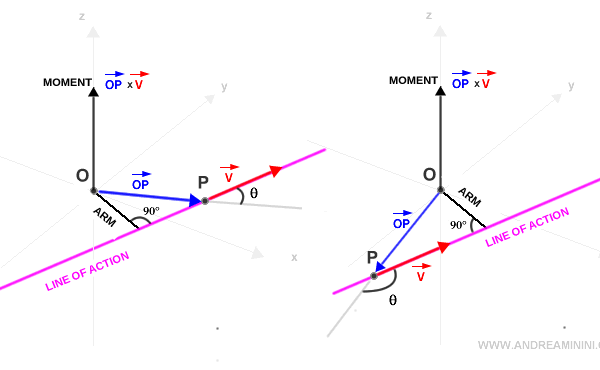
Explication pas à pas
Considérons un vecteur appliqué en un point P et un point de référence O, choisi comme pôle.
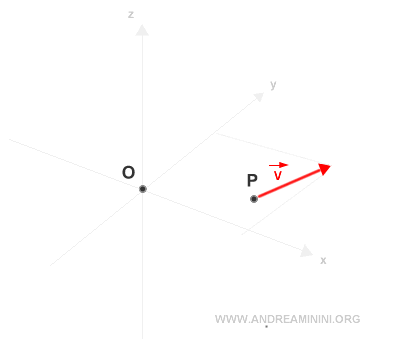
On commence par déterminer le vecteur de position de P par rapport à O.
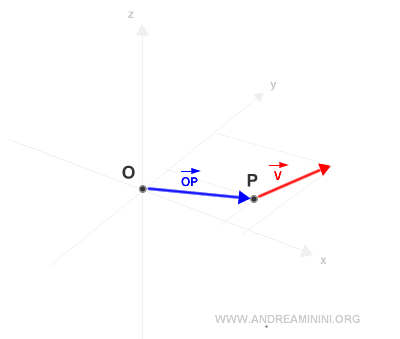
Puis on trace les droites correspondant aux directions des deux vecteurs.
La direction du vecteur v définit sa ligne d’action.
On mesure ensuite l’angle θ entre les deux vecteurs.
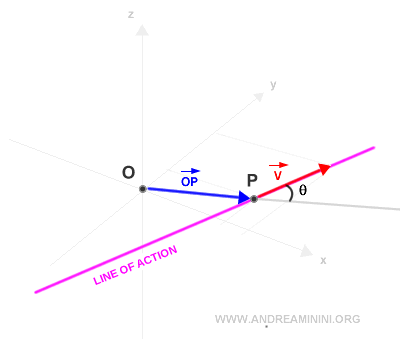
La distance perpendiculaire entre la ligne d’action et le pôle s’appelle le bras de levier.
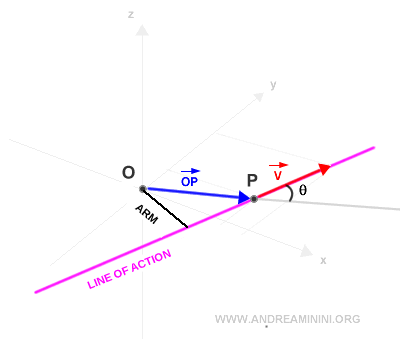
On calcule enfin le produit vectoriel entre OP et v.
On obtient un vecteur perpendiculaire au plan, qui représente le moment du vecteur v par rapport au pôle O.
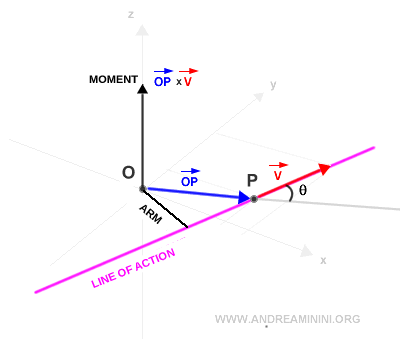
Effet d’un changement de pôle
Le pôle sert de point de référence (ou de repère).

Si l’on remplace O par un nouveau point O’ dans le plan cartésien, le moment du vecteur est modifié.
Le nouveau vecteur moment MO' conserve la même direction que le moment initial, mais sa norme change en général.
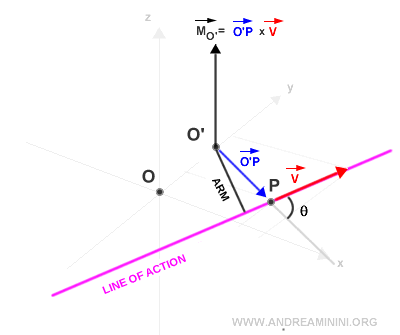
Changer de pôle modifie donc l’angle θ, le bras de levier et la norme du moment.
Les deux moments MO et MO' du vecteur v sont reliés par la relation suivante :
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$
Démonstration
Le moment du vecteur v par rapport à O est :
$$ \vec{M_O} = \vec{OP} × \vec{v} $$
Celui du même vecteur par rapport à O’ est :
$$ \vec{M_{O'}} = \vec{O'P} × \vec{v} $$
Or, le vecteur O’P s’exprime comme la somme des vecteurs O’O et OP.
D’où :
$$ \vec{M_{O'}} = ( \vec{O'O} + \vec{OP} ) × \vec{v} $$
En utilisant la distributivité du produit vectoriel :
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{OP} × \vec{v} $$
Comme MO = OP × v, on obtient :
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$
La relation entre les deux moments du vecteur, calculés par rapport à O et à O’, est ainsi démontrée.
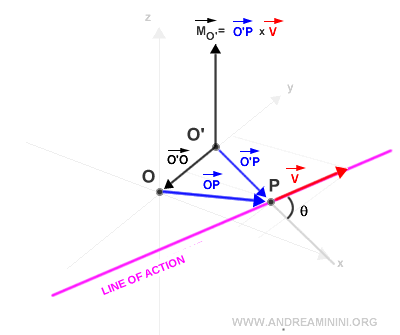
Il en résulte que la norme du nouveau moment |MO'| après changement de repère est :
$$ | \vec{M_{O'}} | = | \vec{O'O} × \vec{v} | + | \vec{M_O} | $$
Remarque. Si, lors du changement de pôle, le vecteur O’O est parallèle à v, le moment n’est pas modifié car le bras de levier reste identique. $$ \vec{O'O} \ || \ \vec{v} \ \ \Rightarrow \ \ M_{O'}=M_O $$ Le schéma suivant illustre ce cas particulier :
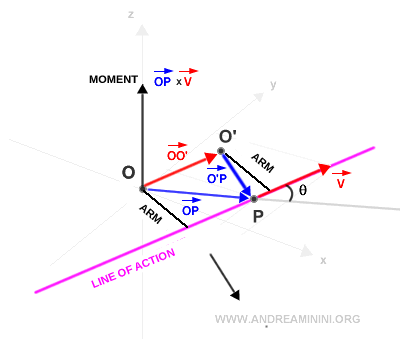
Et ainsi de suite.