Produit vectoriel

Le produit vectoriel dans l’espace tridimensionnel

Le produit vectoriel est une opération particulière entre deux vecteurs qui engendre un troisième vecteur. Lorsqu’on parle du « vecteur \( \vec{u} \) croisé avec le vecteur \( \vec{v} \) », on écrit : $$ \vec{u} \times \vec{v} = \vec{w} $$ On le rencontre parfois également sous la forme : $$ \vec{u} \wedge \vec{v} = \vec{w} $$ Le module du produit vectoriel est donné par : $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$

Cette opération est définie pour deux vecteurs de l’espace euclidien \( \mathbb{R}^3 \) et produit un vecteur unique.

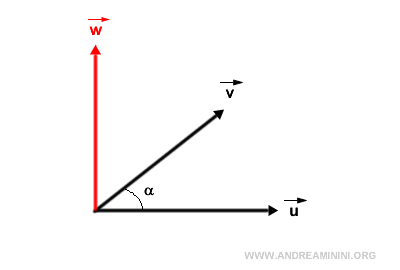
Le vecteur résultant \( \vec{w} \) est orthogonal aux deux vecteurs initiaux, c’est-à-dire perpendiculaire à chacun d’eux.

Par convention, on emploie le symbole « \(\times\) » pour désigner le produit vectoriel, bien que dans certains contextes le symbole « \(\wedge\) » soit également utilisé.

Propriétés du produit vectoriel. La connaissance des propriétés fondamentales du produit vectoriel est indispensable, car elles constituent le socle de l’algèbre vectorielle.

Propriétés géométriques du produit vectoriel

Le vecteur \( \vec{w} \) issu du produit vectoriel présente les caractéristiques suivantes :

• Le module du produit vectoriel, c’est-à-dire \( |\vec{w}| \), correspond à l’aire du parallélogramme formé par les vecteurs \( \vec{u} \) et \( \vec{v} \).
  
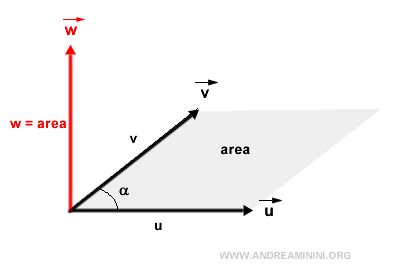
  D’un point de vue trigonométrique, on obtient : $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$ autrement dit, le produit de la norme de \( \vec{u} \) par la composante de \( \vec{v} \) perpendiculaire à \( \vec{u} \).

  Remarque. Cette formule entraîne des conséquences immédiates : si les vecteurs sont colinéaires, leur produit vectoriel est nul, car l’aire du parallélogramme est nulle. En particulier, pour deux vecteurs parallèles (angle 0°) ou antiparallèles (angle 180°), le produit vectoriel est le vecteur nul.
  
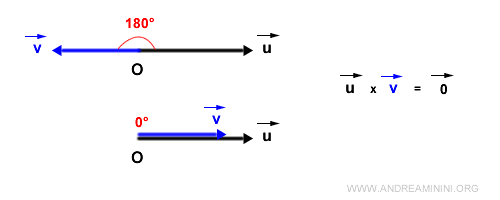
  Si les vecteurs sont orthogonaux (angle de 90°), le module du produit vectoriel est simplement le produit de leurs normes, puisque \( \sin 90^\circ = 1 \).
  
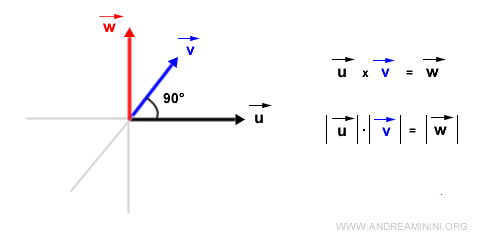
  Enfin, si les vecteurs forment un angle de -90°, le module reste inchangé mais la direction de \( \vec{w} \) s’inverse, car \( \sin(-90^\circ) = -1 \).
  

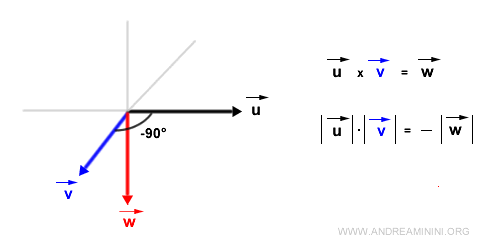
• Direction du produit vectoriel. Le vecteur \( \vec{w} \) est perpendiculaire au plan contenant \( \vec{u} \) et \( \vec{v} \).
  
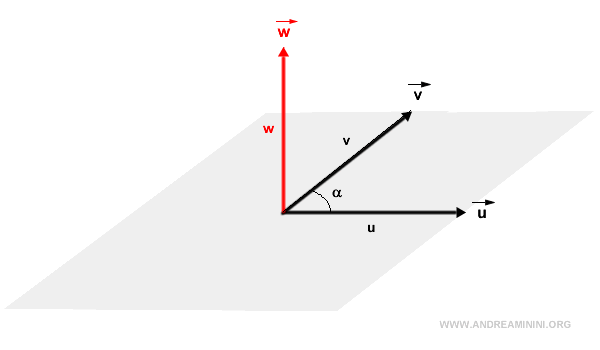
• Orientation du produit vectoriel. Pour fixer le sens de \( \vec{w} \), on utilise la règle de la main droite : le pouce correspond à \( \vec{u} \), l’index à \( \vec{v} \), et le majeur indique la direction de \( \vec{w} \).
  
  

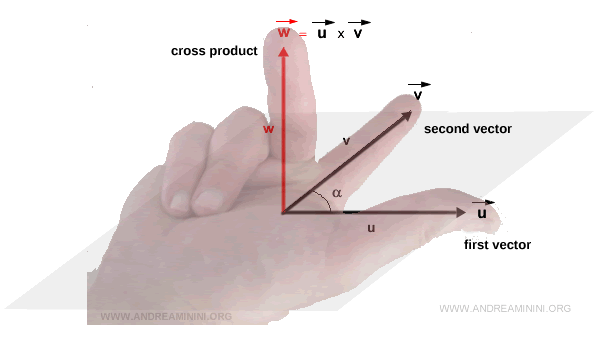
  Remarque. Il est crucial que le pouce soit orienté selon le premier vecteur et l’index selon le second.

  Autre critère
  On considère le plan engendré par les deux vecteurs. Si, vu de dessus, la rotation la plus directe pour amener \( \vec{u} \) vers \( \vec{v} \) est dans le sens antihoraire, alors \( \vec{w} = \vec{u} \times \vec{v} \) pointe vers le haut. Ce principe est souvent appelé règle du tire-bouchon de la main droite.
  
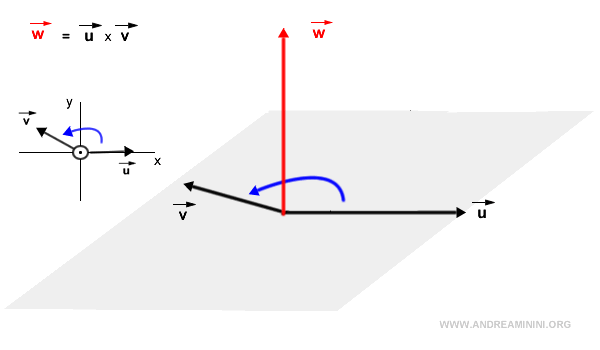
  À l’inverse, si la rotation est horaire, \( \vec{w} \) pointe vers le bas, donc dans la direction opposée au plan du point de vue de l’observateur.
  
  

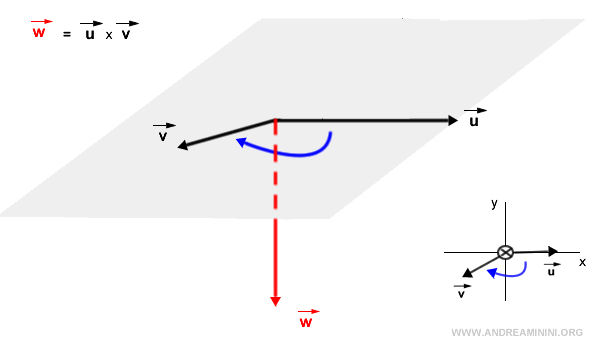
  Remarque. De manière générale, si l’on observe depuis l’extrémité du vecteur \( \vec{w} \) en direction du plan, la rotation la plus directe qui amène \( \vec{u} \) vers \( \vec{v} \) est toujours dans le sens antihoraire.

Calcul du produit vectoriel

Le produit vectoriel peut être calculé de deux façons équivalentes.

Méthode 1 :

Soient :

$$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} , \quad \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} $$

Alors :

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} det \begin{pmatrix} y_1 & y_2 \\ z_1 & z_2 \end{pmatrix} \\ - det \begin{pmatrix} x_1 & x_2 \\ z_1 & z_2 \end{pmatrix} \\ det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \end{pmatrix} $$

Méthode 2 :

Le produit vectoriel peut aussi se mettre sous forme de déterminant :

$$ \vec{v_1} \wedge \vec{v_2} = det \begin{pmatrix} \vec{i} & x_1 & x_2 \\ \vec{j} & y_1 & y_2 \\ \vec{k} & z_1 & z_2 \end{pmatrix} $$

Exemple pratique

Dans \( \mathbb{R}^3 \), considérons :

$$ \vec{v_1} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} , \quad \vec{v_2} = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Calculons leur produit vectoriel \( \vec{v_1} \times \vec{v_2} \) par les deux méthodes.

Méthode 1

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} det \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} \\ - det \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} \\ det \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} \end{pmatrix} $$

En développant :

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} 2 \cdot 2 - (-3) \cdot 1 \\ - (1 \cdot 2 - 1 \cdot 1) \\ 1 \cdot (-3) - 1 \cdot 2 \end{pmatrix} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} $$

On obtient un vecteur orthogonal aux deux vecteurs initiaux, donc perpendiculaire à chacun d’eux.

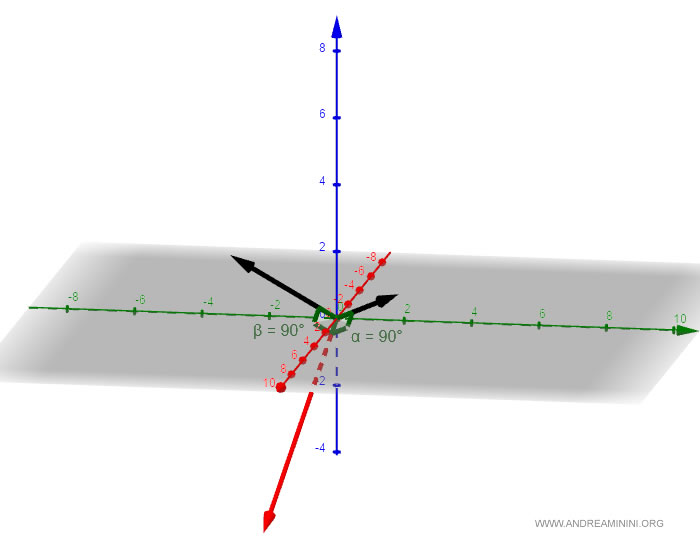
Le produit scalaire de deux vecteurs orthogonaux est nul : $$ \left\langle \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \right\rangle = 7 \cdot 1 - 2 - 5 = 0 $$ $$ \left\langle \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} \right\rangle = 7 + 3 - 10 = 0 $$ Ce qui confirme que le vecteur obtenu est bien orthogonal aux deux vecteurs de départ.

Méthode 2

Partons de :

$$ \vec{v_1} \wedge \vec{v_2} = det \begin{pmatrix} \vec{i} & 1 & 1 \\ \vec{j} & 2 & -3 \\ \vec{k} & 1 & 2 \end{pmatrix} $$

En développant ce déterminant :

$$ \vec{v_1} \wedge \vec{v_2} = \vec{i} \, det \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} - \vec{j} \, det \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} + \vec{k} \, det \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} $$

On obtient : $$ \vec{v_1} \wedge \vec{v_2} = 7 \vec{i} - \vec{j} - 5 \vec{k} $$

Ainsi, en coordonnées : $$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} $$

Le résultat est identique à celui trouvé par la première méthode, ce qui confirme la cohérence du calcul.

Propriétés du produit vectoriel

Le produit vectoriel, noté \( \vec{a} \times \vec{b} \), possède plusieurs propriétés fondamentales :

Anticommutativité
Le produit vectoriel n’est pas commutatif : $$ \vec{a} \wedge \vec{b} = -\vec{b} \wedge \vec{a} $$
Distributivité par rapport à l’addition vectorielle
$$ \vec{a} \wedge (\vec{b} + \vec{c}) = (\vec{a} \wedge \vec{b}) + (\vec{a} \wedge \vec{c}) $$

D’autres propriétés essentielles :

$$ k \cdot \vec{a} \wedge \vec{b} = \vec{a} \wedge (k \cdot \vec{b}) = k \cdot (\vec{a} \wedge \vec{b}) $$ $$ \langle \vec{a}, \vec{a} \wedge \vec{b} \rangle = \langle \vec{b}, \vec{a} \wedge \vec{b} \rangle = 0 $$ $$ \| \vec{a} \wedge \vec{b} \|^2 = \| \vec{a} \|^2 \cdot \| \vec{b} \|^2 - \langle \vec{a}, \vec{b} \rangle^2 $$ $$ \| \vec{a} \wedge \vec{b} \| = \| \vec{a} \| \cdot \| \vec{b} \| \cdot \sin(\widehat{\vec{a}, \vec{b}}) $$

Une conséquence immédiate est la suivante : deux vecteurs sont parallèles si, et seulement si, leur produit vectoriel est nul.

$$ \vec{a} \wedge \vec{b} = 0 \ \ \Leftrightarrow \ \ \vec{a} || \vec{b} $$

Le produit vectoriel s’annule dans deux situations :

• si l’un des vecteurs est nul : $$ \vec{a} \wedge \vec{b} = 0 \quad \text{si} \quad \vec{a} = \vec{0} \ \text{et/ou} \ \vec{b} = \vec{0} $$
• si les deux vecteurs sont parallèles ou confondus, c’est-à-dire linéairement dépendants : $$ \vec{a} \wedge \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

Ainsi, sauf cas trivial du vecteur nul, un produit vectoriel nul caractérise toujours deux vecteurs parallèles.

Non-associativité. Le produit vectoriel n’est pas associatif : l’ordre des opérations est donc déterminant. $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) \ne (\vec{a} \wedge \vec{b}) \wedge \vec{c} $$

Produit vectoriel triple

On appelle produit vectoriel triple une opération dans laquelle l’un des facteurs est lui-même un produit vectoriel : $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) $$

L’usage des parenthèses est indispensable, puisque le produit vectoriel n’est pas associatif. En particulier : $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) \ne (\vec{a} \wedge \vec{b}) \wedge \vec{c} $$

Le produit vectoriel triple se développe grâce à la formule de Lagrange : $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) = (\vec{a} \cdot \vec{c}) \vec{b} - (\vec{a} \cdot \vec{b}) \vec{c} $$ Autrement dit : $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) = \vec{b} (\vec{a} \cdot \vec{c}) - \vec{c} (\vec{a} \cdot \vec{b}) $$ On notera que, bien que l’expression initiale contienne un produit vectoriel, son développement ne fait intervenir que des produits scalaires. Le résultat reste toutefois un vecteur. Un moyen mnémotechnique classique consiste à retenir : ACB - ABC ou BAC - CAB.

Exemple

Considérons trois vecteurs :

$$ \vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix}, \quad \vec{c} = \begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} $$

On cherche à calculer \( \vec{a} \wedge (\vec{b} \wedge \vec{c}) \). On commence par le produit vectoriel interne :

$$ \vec{b} \wedge \vec{c} = \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix} $$

Puis : $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \wedge \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix} $$

Enfin, en développant :

$$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) = \begin{pmatrix} -24 \\ -6 \\ 12 \end{pmatrix} $$

Produit vectoriel des vecteurs unitaires de la base cartésienne

On définit le produit vectoriel des vecteurs unitaires de la base canonique de la façon suivante :

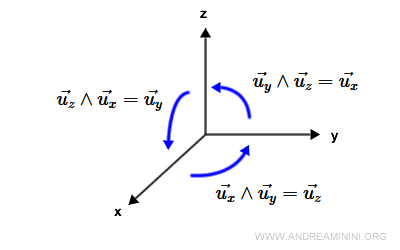
On obtient notamment :

$$ \vec{u_x} \wedge \vec{u_y} = \vec{u_z}, \quad \vec{u_y} \wedge \vec{u_x} = -\vec{u_z} $$

$$ \vec{u_y} \wedge \vec{u_z} = \vec{u_x}, \quad \vec{u_z} \wedge \vec{u_y} = -\vec{u_x} $$

$$ \vec{u_z} \wedge \vec{u_x} = \vec{u_y}, \quad \vec{u_x} \wedge \vec{u_z} = -\vec{u_y} $$

En particulier, le produit vectoriel d’un vecteur unitaire par lui-même est toujours nul : $$ \vec{u_x} \wedge \vec{u_x} = \vec{0}, \quad \vec{u_y} \wedge \vec{u_y} = \vec{0}, \quad \vec{u_z} \wedge \vec{u_z} = \vec{0} $$

Formule générale du produit vectoriel

Dans \( \mathbb{R}^3 \), le produit vectoriel de deux vecteurs s’écrit : $$ \vec{a} \wedge \vec{b} = (a_y b_z - a_z b_y ) \vec{u_x} + (a_z b_x - a_x b_z) \vec{u_y} + (a_x b_y - a_y b_x) \vec{u_z} $$

Cette expression est particulièrement pratique lorsqu’on calcule directement à partir des composantes.

Moyen mnémotechnique. Pour la retrouver rapidement, on construit la matrice : $$ \begin{pmatrix} u_x & u_y & u_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{pmatrix} $$ et l’on applique la règle de Sarrus, ce qui conduit à : $$ (a_y b_z - a_z b_y ) \vec{u_x} + (a_z b_x - a_x b_z ) \vec{u_y} + (a_x b_y - a_y b_x ) \vec{u_z} $$

Démonstration

En développant : $$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z}, \quad \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$ puis en appliquant la distributivité, on obtient successivement les termes élémentaires, que l’on regroupe à l’aide des identités fondamentales : $$ \vec{u_x} \wedge \vec{u_y} = \vec{u_z}, \quad \vec{u_y} \wedge \vec{u_x} = -\vec{u_z}, \quad \vec{u_y} \wedge \vec{u_z} = \vec{u_x}, \quad \vec{u_z} \wedge \vec{u_y} = -\vec{u_x}, \quad \vec{u_z} \wedge \vec{u_x} = \vec{u_y}, \quad \vec{u_x} \wedge \vec{u_z} = -\vec{u_y} $$

On retrouve ainsi la formule générale : $$ (a_y b_z - a_z b_y) \vec{u_x} + (a_z b_x - a_x b_z) \vec{u_y} + (a_x b_y - a_y b_x) \vec{u_z} $$